20240130 A 组模拟赛 部分题解
前言
T3 是模拟赛原,这里就不重复了。
T1
瞪眼法做题。这里讲一下我赛时怎么猜出部分结论以及怎么合理地从这个结论猜到答案。
首先从简单开始,考虑假如在前 $r$ 行 $c$ 列里放一个 $1$,整个矩阵会如何改变。
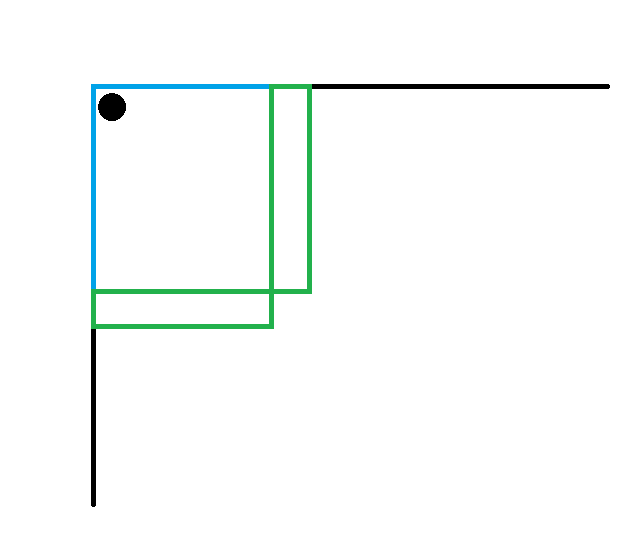
容易发现两绿色矩阵里面都必须放恰好一个,且不能存在某 $r\times c$ 的子矩阵同时包含两者。
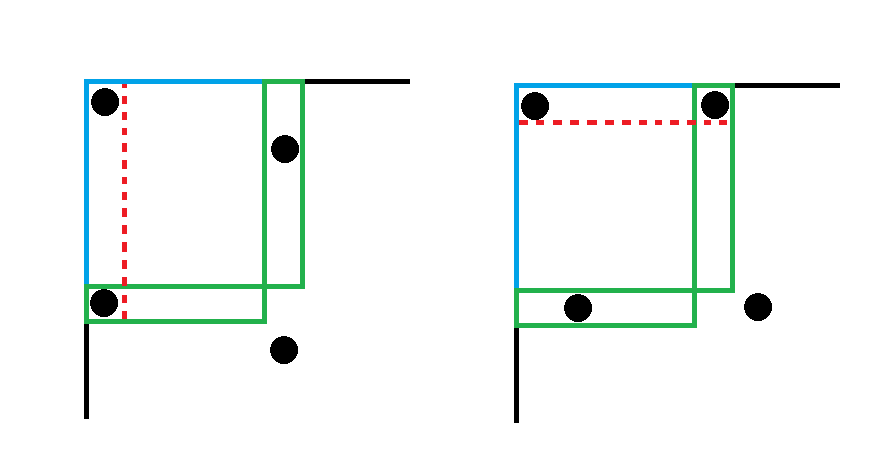
首先两边都对齐最开始放的那个显然符合要求,并且容易发现若一边不对齐则另一边必定对齐。更进一步的,若最开始是横向对齐,那么之后所有都会与前 $c$ 列横向对齐,纵向同理。
考虑推广到多个。但显然多个有横有纵会产生冲突(我赛时就卡这里了),怎么解决呢?
注意到“$1$ 的个数相同”等价于“$0$ 的个数相同”,那么对于空格也必定会有类似的性质。考虑把刚刚影响了的空格找出来。
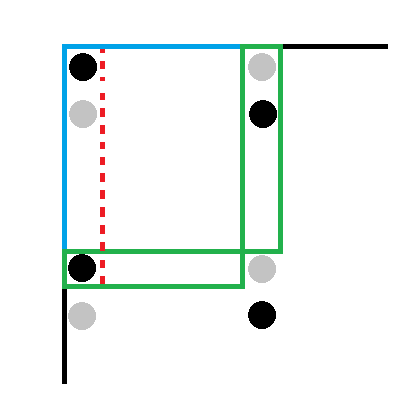
显然这些空格是不能填横向对齐的 $1$ 的(不然就会出现“重复填在同一格”的情况)。
这下事情就好办了,直接 $2^{rc}$ 枚举前 $r\times c$ 的矩阵中每一格是与其它格子纵向对齐还是横向对齐的,然后统计每一列纵向对齐的个数和每一行横向对齐的个数。下面暂时只考虑每一列的纵向对齐。
设第 $i$ 列有 $col_{i}$ 个纵向对齐的格子,那么枚举其中有 $j$ 个 $1$,单独一组的填法就有 $\sum_{j=0}^{col_i}\binom{col_i}{j}$ 种,并且显然有 $\left\lceil\frac{m-i}{c}\right\rceil$ 组,设这个数是 $num$,纵向的纵方案数就是 $\prod_{i=1}^{r}\sum_{j=1}^{col_i}\binom{col_i}{j}^{num}$。
而横向的类似,但有一点要注意,就是可能出现一整列都是 $1$的情况。这样的情况会在该格子归为纵向时仍被算一遍。这个可以容斥解决,就枚举有多少列不变即可。
复杂度最优可以做到 $O(2^{rc}rc)$,但是需要一些预处理,我懒得写了,就带了一堆奇奇怪怪的 $\log$,照样能过。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
//const int N=4,inf=0x3f3f3f3f;
int n,m,r,c,mod,ans;
int col[4],row[4],binom[5][5];
int ksm(int a,int b){
int c=1;
while(b){
if(b&1) c=1ll*a*c%mod;
a=1ll*a*a%mod;
b>>=1;
}
return c;
}
void upd(int &a,int b){
a+=b;
if(a>mod) a-=mod;
if(a<0) a+=mod;
}
signed main(){
n=read();m=read();r=read();c=read();mod=read();
binom[0][0]=1;
forup(i,1,max(r,c)){
binom[i][0]=1;
forup(j,1,i){
binom[i][j]=(binom[i-1][j-1]+binom[i-1][j])%mod;
}
}
forup(msk,0,(1<<(r*c))-1){
mem(col,0);mem(row,0);
forup(i,0,r-1){
forup(j,0,c-1){
if(msk&(1<<(i*c+j))){
++row[i];
}else{
++col[j];
}
}
}
int res=1;
forup(i,0,c-1){
int num=(m-i+c-1)/c,t=0;
forup(j,0,col[i]){
upd(t,ksm(binom[col[i]][j],num));
}
res=1ll*res*t%mod;
}
forup(i,0,r-1){
int num=(n-i+r-1)/r,t=0;
forup(k,0,row[i]){
int p=1ll*(k&1?mod-1:1)*binom[row[i]][k]%mod*ksm(2,k)%mod;
forup(j,0,row[i]-k){
upd(t,1ll*p*ksm(binom[row[i]-k][j],num)%mod);
}
}
res=1ll*res*t%mod;
}
(ans+=res)%=mod;
}
printf("%d\n",ans);
}
T2
神秘题,感觉根本想不到啊。
首先,每个询问都在树上跑是很困难的,考虑把询问离线下来放在一起考虑。观察部分分,发现有一个“链”的部分分,考虑这样的链具有什么样的性质。
容易发现,这样的链相当于维护一个 $x$,每次从底到顶计算 $x\gets|x-b_i|+a_i$,可以想到用线段树维护询问的时间轴,然后做一个“整体减 $b_i$ 后取绝对值”的操作。
这就是这道题最神秘的地方了。这可以 segbeats 维护,因为每次递归区间内的极差都会至少减少 $1$,然后和 segbeats 类似地进行势能分析即可(这就是为什么这道题 $a_i$ 比较小),由于极差之和是 $nv\log q$ 的,容易发现总复杂度是 $O((n+q)V\log q)$。
考虑树的情况怎么做,会了前面的之后用屁股都能想到线段树合并,具体合并方式是每次遇到某一边是完整的一个区间就开始进行 segbeats 的操作。
考虑复杂度证明,若对两个结点进行 segbeats 的操作说明其中一边势能为 $0$,而另一边每进入一个区间势能就会减少至少 $1$。而每个询问操作至多增加 $\log q$ 的势能(考虑线段树上“未被完全覆盖”的结点数量),那么时间复杂度仍是 $O((n+q)v\log q)$。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
using pii=pair<int,int>;
#define fi first
#define se second
#define mkp make_pair
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=1e5+5,inf=0x3f3f3f3f;
int n,q,a,ch[N][2],ans[N];
struct SegTree{
#define mid ((l+r)>>1)
#define lson l,mid,ls[id]
#define rson mid+1,r,rs[id]
int querymax[N*45],querymin[N*45],addmark[N*45],multmark[N*45],ls[N*45],rs[N*45],root[N],cntn;
int New(){
int nw=++cntn;
querymax[nw]=querymin[nw]=0;
addmark[nw]=0;multmark[nw]=1;
return nw;
}
void PushUp(int id){
querymax[id]=-inf;querymin[id]=inf;
if(ls[id]){
querymax[id]=max(querymax[id],querymax[ls[id]]);
querymin[id]=min(querymin[id],querymin[ls[id]]);
}
if(rs[id]){
querymax[id]=max(querymax[id],querymax[rs[id]]);
querymin[id]=min(querymin[id],querymin[rs[id]]);
}
}
void modi(int id,int mul,int add){
if(mul<0) swap(querymax[id],querymin[id]);
querymax[id]*=mul;querymax[id]+=add;
querymin[id]*=mul;querymin[id]+=add;
addmark[id]*=mul;addmark[id]+=add;
multmark[id]*=mul;
}
void PushDown(int id){
if(addmark[id]==0&&multmark[id]==1) return;
if(!ls[id]) ls[id]=New();
if(!rs[id]) rs[id]=New();
modi(ls[id],multmark[id],addmark[id]);
modi(rs[id],multmark[id],addmark[id]);
multmark[id]=1;addmark[id]=0;
}
void Update(int L,int R,int X,int l,int r,int &id){
if(L>R) return;
if(!id) id=New();
if(L<=l&&r<=R){
modi(id,1,X);
return;
}
PushDown(id);
if(L<=mid) Update(L,R,X,lson);
if(mid< R) Update(L,R,X,rson);
PushUp(id);
}
int Merge(int u,int v){
if(!u||!v) return u|v;
if(querymin[u]==querymax[u]){
if(querymax[v]<=querymin[u]){
modi(v,-1,querymin[u]);
return v;
}else if(querymin[v]>=querymax[u]){
modi(v,1,-querymax[u]);
return v;
}
}
if(querymin[v]==querymax[v]){
if(querymax[u]<=querymin[v]){
modi(u,-1,querymin[v]);
return u;
}else if(querymin[u]>=querymax[v]){
modi(u,1,-querymax[v]);
return u;
}
}
PushDown(u);PushDown(v);
ls[u]=Merge(ls[u],ls[v]);
rs[u]=Merge(rs[u],rs[v]);
PushUp(u);
return u;
}
void Ans(int l,int r,int id){
if(l==r){
ans[l]=querymin[id];
return;
}
PushDown(id);
Ans(lson);Ans(rson);
}
}mt;
vector<pii> momo[N];
void dfs(int x){
if(ch[x][0]){
dfs(ch[x][0]);dfs(ch[x][1]);
mt.root[x]=mt.Merge(mt.root[ch[x][0]],mt.root[ch[x][1]]);
}
int sz=momo[x].size()-1;
forup(i,0,sz-1){
mt.Update(momo[x][i].fi,momo[x][i+1].fi-1,momo[x][i].se,1,q,mt.root[x]);
}
}
signed main(){
n=read();
forup(i,1,n){
ch[i][0]=read();ch[i][1]=read();
}
forup(i,1,n){
int a=read();
momo[i].push_back(mkp(1,a));
}
q=read();
forup(i,1,q){
int u=read(),x=read();
momo[u].push_back(mkp(i,x));
}
forup(i,1,n){
momo[i].push_back(mkp(q+1,0));
}
dfs(1);
mt.Ans(1,q,mt.root[1]);
forup(i,1,q){
printf("%d\n",ans[i]);
}
}