20231204 A 组模拟赛 题解
前言
感觉升到 A 组后模拟赛质量高了好多。
T3
很智慧的一道题。
考虑一个暴力 DP,设 $dp_{i,j}$ 表示第 $i$ 天,换乘 $j$ 次的最大贡献是多少。转移很简单,就是考虑现在的城市是 $j\bmod k$,然后下一步换不换乘。复杂度 $O(n^2)$,有 25pts。
考虑如何优化。注意到这道题 $k$ 的范围很小,但是上面的方法复杂度和 $k$ 一点关系都没有。如何和 $k$ 扯上关系呢?考虑把 $j$ 写成 $pk+q$ 的形式,因为对于同一个 $q$,转移是相同的,所以考虑 $p$ 的取值。容易猜到 $dp_{i,pk+q}$ 在固定 $i,p$ 后,可能是关于 $p$ 上凸的(感性来说,最大值肯定在中间取到),考虑证明。
首先一个和上凸($y_{i+1}-y_{i}$ 关于 $i$ 单调不增,不用除以 $x$ 是因为相邻两个 $x$ 之差均为 $1$)等价的命题是 $\forall i\in(1,n),\frac{y_{i+1}+y_{i-1}}{2}\le y_i$,代数证明可以考虑两边乘以二然后移项,几何证明考虑取 $(x_{i-1},y_{i-1}),(x_{i+1},y_{i+1})$ 的中点。
回到原问题,容易发现若令 $V_p=dp_{i,pk+q}$,那么假如我们能证明 $\frac{V_{i-1}+V_{i+1}}{2}\le V_i$,就能说明 $V$ 是上凸的。考虑把 $V_{i-1},V_{i+1}$ 的路径并排放在一起:
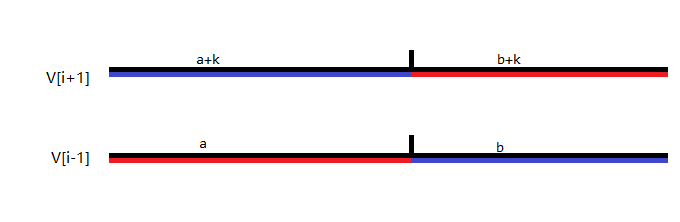
那么必定能找到一个分界点,使得分界点左侧,$V_{i+1}$ 和 $V_{i-1}$ 的换乘次数之差是 $k$,那么右侧换乘次数之差同样也是 $k$。那么显然在分界点处的位置是相同的。此时把两段分开重新拼起来(就是两红色线段和两蓝色线段)换乘次数必定是 $ik+q$,即一个换乘次数正确的 $V_i$。显然两方案中必定有一个大于等于 $\frac{V_{i-1}+V_{i+1}}{2}$,得证。
考虑上凸之后我们能干什么(这一步很不自然我也不知道题解怎么想到的,或许是因为上一步的证明让人想到把一个序列拆成两半?),可以想到,若把某个方案分成两半,合起来的时候就是一个 $(\max,+)$ 卷积。具体来说,设 $(l,r,x,y)$ 表示从 $l$ 到 $r$,换乘 $x$ 次,获利为 $y$ 的方案,那么 $(l,r,x,y)$ 必定能从 $(l,mid,x',y')+(mid+1,x-x',y-y')$(或者在中间换乘一次,$(l,mid,x',y')+(mid+1,r,x-x'+1,y-y')$)得到。而凸性和 $(\max,+)$ 卷积让人联想到闵可夫斯基和,考虑把刚刚很粗糙的猜想细化,并套入关于 $p$ 的凸性。
由于区间的左右端点不固定,所以还要记录起点和终点的城镇 $S,E$(容易发现 $q$ 就是 $(E+m-S)\bmod m$),那么容易想到固定 $(l,r,S,E)$,这样 $V$ 关于 $p$ 就是上凸的。然后分治,合并时每局中间点 $M$,求闵可夫斯基和即可。
这里有一个细节,合并是从 $(l,mid,S,M)+(mid+1,r,M,E)/(mid+1,r,(M+1)\bmod m,E)$ 转移,注意 $S\to M(\to (M+1)\bmod m)\to E$ 会不会额外绕一圈。
时间复杂度 $O(k^3\sum\frac{len}{k})=O(k^2n\log n)$,4s 还是随便过的。然后空间每次可以复用之前的,貌似可以做到 $O(k^2\frac{n}{k})=O(nk)$,但是我空间貌似写挂了,但是无所谓能过就行。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(i64 i=(s);i<=(e);i++)
#define fordown(i,s,e) for(i64 i=(s);i>=(e);i--)
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
using i64=long long;
#define gc getchar()
inline i64 read(){
i64 x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const i64 N=1e5+5,inf=0x3f3f3f3f;
i64 n,m,q;
i64 a[7][N];
vector<i64> f[N<<2][7][7];
void work(vector<i64>& vec,vector<i64> &vls,vector<i64> &vrs,i64 flag){
if(vls.empty()||vrs.empty()) return;
i64 ll=1,rr=1,nw=vls[0]+vrs[0],lsz=vls.size(),rsz=vrs.size();
vec[flag]=max(vec[flag],nw);
forup(i,1,lsz+rsz-2){
if(rr==rsz||(ll<lsz&&vls[ll]-vls[ll-1]>(rr==0?vrs[rr]:vrs[rr]-vrs[rr-1]))){
nw+=vls[ll]-vls[ll-1];
++ll;
}else{
nw+=(rr==0?vrs[rr]:vrs[rr]-vrs[rr-1]);
++rr;
}
vec[i+flag]=max(vec[i+flag],nw);
}
}
bool chk(i64 st,i64 ed,i64 m1,i64 m2){
i64 len=(m1+m-st)%m+(ed+m-m2)%m+(m1!=m2);
return len>=m;
}
void solve(i64 l,i64 r,i64 id){
if(l==r){
forup(i,0,m-1){
f[id][i][i].push_back(a[i][l]);
}
return;
}
i64 mid=(l+r)>>1,ls=id<<1,rs=id<<1|1;
solve(l,mid,ls);solve(mid+1,r,rs);
forup(p,0,m-1){
forup(q,0,m-1){
if(r-l<(q+m-p)%m) continue;
vector<i64> &vec=f[id][p][q];
vec.resize((r-l-(q+m-p)%m)/m+1);
forup(mm,0,m-1){
work(vec,f[ls][p][mm],f[rs][mm][q],chk(p,q,mm,mm));
work(vec,f[ls][p][mm],f[rs][(mm+1)%m][q],chk(p,q,mm,mm+1));
}
}
}
forup(p,0,m-1){
forup(q,0,m-1){
f[ls][p][q].clear();f[ls][p][q].shrink_to_fit();
f[rs][p][q].clear();f[rs][p][q].shrink_to_fit();
}
}
}
signed main(){
n=read();m=read();q=read();
forup(i,0,m-1){
forup(j,1,n){
a[i][j]=read();
}
}
solve(1,n,1);
forup(Case,1,q){
i64 k=read()-1;
i64 pp=k/m,qq=k%m;
printf("%lld\n",f[1][0][qq][pp]);
}
}