20231026 B 组模拟赛 题解
前言
T1 是巨大分类讨论,但目前大家还没找到一个真正正确的构造方案,鉴定为改了没什么营养。
T2
很妙的题。
首先核心思路是固定上下端点 $x_1,x_2$ 和左端点 $y_1$,求出有多少个右端点满足条件。
你可以发现没有空穴和有且仅有一个连通块是可以分开处理的。
先处理比较简单的,“没有空穴”怎么处理呢?容易想到对于整张图上的每一个空穴,我们很容易找到完全包含它的最小矩形。那么完全包含这样的矩形的矩形就是有空穴的,另外容易发现这样的矩形是不重合的,可以直接存到 $(x_1,x_2,y_1)$ 的位置。也就是说,我们可以考虑对 $(x_1,x_2,y_1)$ 的三元组求出它的右端点到哪个位置完整包含第一个空穴,设这个位置为 $lim_{x_1,x_2,y_1}$,那么必定更往右的都有空穴。
而这其实是是很容易 $O(n^3)$ 做的:
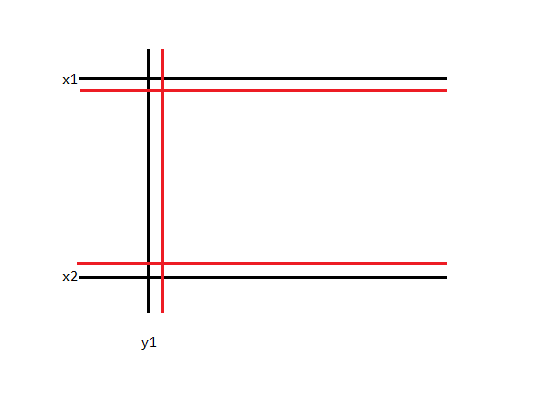
考虑 $(x_1,x_2,y_1)$ 围出来的区域中,空穴除了 $(x_1+1,x_2,y_1),(x_1,x_2-1,y_1),(x_1,x_2,y_1+1)$ 三组围出来的以外,就只有它自己了。那么类似于区间 dp,可以 $O(1)$ 转移。
接下来考虑有且仅有一个连通块如何处理。这个要用到一个叫“平面图欧拉公式”的东西。
公式内容很简单,对于一个连通的有至少一个点的平面图,$V+F-E=2$,其中 $V$ 是图中点的个数,$F$ 是面的个数,$E$ 是边的个数。平面图的定义是能画在平面上的图,即任意两条边相交都会产生一个新的点,或者说从 OI 的 graph 视角来看,是边在结点之外均不相交的图。
考虑证明欧拉公式,这里做一个简单证明:
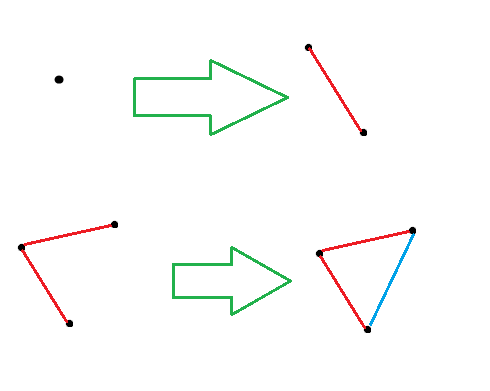
首先考虑单个点,显然 $V+F-E=2$(因为本来平面就是一个面)。
而考虑加一条边,容易发现一条边必定使点数 $+1$ 或使面数 $+1$,那么显然上式的值是不会变的。
并且如果你不算初始的平面的话,$V+F-E$ 就是平面图连通块个数!
注意到题目对于连通块的定义是四连通块,即每个黑色方格向上下左右黑色方格连边组成的连通块,恰好符合平面图的定义。那么我们可以考虑维护 $V+F-E$ 来判断矩阵内连通块个数。
回到我们的核心思路,即我们在固定 $x_1,x_2$ 后求出有多少个 $y_2$ 能和枚举的 $y_1$ 匹配。由于固定了 $x_1,x_2$,那么久只需要处理一个一维的问题了,很容易想到维护前缀和。
首先对于一个前缀,边和点的数量是好统计的,但是面的数量不好做,怎么办呢?注意到合法区间是没有空穴的,而除去空穴,所有的面都是 $2\times 2$ 的矩形!这就非常好做了。设 $v_i$ 为 $1\sim i$ 的前缀点的个数(即黑色方格的个数)。为方便前缀和,边要统计两种,设 $e1_i$ 为竖着的边的个数(即 $a_{x,y}=1$ 且 $a_{x+1,y}=1$,并且都在 $x_1,x_2$ 范围内),$e2_i$ 为横着的边的个数(即 $a_{x,y}=1$ 且 $a_{x,y-1}=1$,并且 $y\le i$,即往前统计)。然后类似于 $e2$,我们定义 $f_i$ 为 $2\times 2$ 面的个数,并且同样是往前统计。
那么一个 $y_2$ 能和 $y_1$ 匹配,当且仅当 $(v_{y_2}-v_{y_1-1})+(f_{y_2}-f_{y_1})-(e1_{y_2}-e1_{y_1-1})-(e2_{y_2}-e2_{y_1})=1$(注意有哪些下标是 $y_1$,哪些是 $y_1-1$),即 $(v_{y_2}+f_{y_2}-e1_{y_2}-e2_{y_2})-(v_{y_1-1}+f_{y_1}-e1_{y_1-}-e2_{y_1})=1$,且 $y_2<lim_{x_1,x_2,y_2}$。
容易发现,随着 $y_1$ 的减小,$lim_{x_1,x_2,y_2}$ 是单调不增的,那么可以类似于滑动窗口的做,由于 $v_{y_2}+f_{y_2}-e1_{y_2}-e2_{y_2}$ 的值域大约是 $[-n^2,2n^2]$,你可以直接开个数组记每个值出现了多少次,复杂度 $O(n^3)$。
注意 $v,f,e1,e2$ 每次单独求复杂度是错的,可以考虑先纵向求出每一列的答案然后每次扫的时候再拼成前缀和。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(i64 i=(s);i<=(e);i++)
#define fordown(i,s,e) for(i64 i=(s);i>=(e);i--)
#define y1 y114514
using namespace std;
using i64=long long;
#define gc getchar()
inline i64 read(){
i64 x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const i64 N=305,inf=0x3f3f3f3f;
i64 n,m,a[N][N],vis[N][N],ans,lim[N][N][N];
char str[N];
i64 nxt[4][2]={
{0,1},{1,0},{0,-1},{-1,0}
};
struct Node{
i64 u,d,l,r;
};
Node dfs(i64 x,i64 y){
vis[x][y]=1;
Node res=Node{x,x,y,y};
forup(i,0,3){
i64 nx=x+nxt[i][0],ny=y+nxt[i][1];
if(nx<1||nx>n||ny<1||ny>m||a[nx][ny]||vis[nx][ny]) continue;
Node gt=dfs(nx,ny);
res.u=min(res.u,gt.u);
res.d=max(res.d,gt.d);
res.l=min(res.l,gt.l);
res.r=max(res.r,gt.r);
}
return res;
}
struct Negative_index{
i64 c[N*N*4];
i64& operator [](const i64 &p){
return c[p+N*N*2];
}
}cnt;
i64 pv[N][N],pf[N][N],pe1[N][N],pe2[N][N];
i64 cv[N],cf[N],ce1[N],ce2[N];
signed main(){
n=read();m=read();
forup(i,1,n){
scanf(" %s",str+1);
forup(j,1,m){
a[i][j]=(str[j]=='1');
}
}
forup(i,1,n+1){
forup(j,i-1,n){
forup(k,1,m+1){
lim[i][j][k]=m;
}
}
}
forup(i,1,n){
forup(j,1,m){
if(vis[i][j]||a[i][j]) continue;
Node res=dfs(i,j);
lim[res.u-1][res.d+1][res.l-1]=min(lim[res.u-1][res.d+1][res.l-1],res.r);
}
}
forup(len,1,n){
forup(i,1,n-len+1){
i64 j=i+len-1;
fordown(k,m,1){
lim[i][j][k]=min({lim[i][j][k],lim[i+1][j][k],lim[i][j-1][k],lim[i][j][k+1]});
}
}
}
forup(y,1,m){
forup(i,1,n){
pv[i][y]=pv[i-1][y]+a[i][y];
pe1[i][y]=pe1[i-1][y]+(a[i][y]&a[i][y-1]);
}
forup(i,1,n-1){
pe2[i][y]=pe2[i-1][y]+(a[i][y]&a[i+1][y]);
pf[i][y]=pf[i-1][y]+(a[i][y]&a[i+1][y]&a[i][y-1]&a[i+1][y-1]);
}
}
forup(l,1,n){
forup(r,l,n){
i64 ll=m;
cv[0]=cf[0]=ce1[0]=ce2[0]=0;
forup(y,1,m){
cv[y]=cv[y-1]+pv[r][y]-pv[l-1][y];
cf[y]=cf[y-1]+pf[r-1][y]-pf[l-1][y];
ce1[y]=ce1[y-1]+pe1[r][y]-pe1[l-1][y];
ce2[y]=ce2[y-1]+pe2[r-1][y]-pe2[l-1][y];
}
fordown(y,m,1){
while(ll>lim[l][r][y]){
cnt[cv[ll]+cf[ll]-ce1[ll]-ce2[ll]]--;
--ll;
}
cnt[cv[y]+cf[y]-ce1[y]-ce2[y]]++;
ans+=cnt[cv[y-1]+cf[y]-ce1[y]-ce2[y-1]+1];
}
while(ll>=1){
cnt[cv[ll]+cf[ll]-ce1[ll]-ce2[ll]]--;
--ll;
}
}
}
printf("%lld\n",ans);
}
T3
容斥板子题。
首先每条路径都是丰富多彩的这个条件很难做,不妨考虑用总的涂色方案数减去有任意一条路径不是丰富多彩的的方案数。
那么套路地,我们每次钦定一个集合 $S$ 中的路径不是丰富多彩的,设这样的方案数为 $f(S)$,那么答案就是:
$$\sum_{S}(-1)^{|S|}f(S)$$
然后考虑这个 $f(S)$ 怎么算。其实很简单,我们可以很简单并查集求出有多少个必须涂同一种颜色的集合,然后快速幂一下就做完了。
复杂度 $O(2^mn\log n)$。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
using pii=pair<int,int>;
#define fi first
#define se second
#define mkp make_pair
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=65,inf=0x3f3f3f3f,mod=1e9+7;
int n,m,k,ans;
int ksm(int a,int b){
int c=1;
while(b){
if(b&1) c=1ll*a*c%mod;
a=1ll*a*a%mod;
b>>=1;
}
return c;
}
vector<pii> e[N];
vector<int> pa[20];
bool dfs(int x,int fa,int pp,int ed){
if(x==ed) return true;
for(auto i:e[x]){
if(i.fi==fa) continue;
pa[pp].push_back(i.se);
if(dfs(i.fi,x,pp,ed)) return true;
pa[pp].pop_back();
}
return false;
}
int ppcnt(int x){
int res=0;
while(x){
x-=x&-x;
++res;
}
return res;
}
int fa[N];
int getfa(int x){return x==fa[x]?x:fa[x]=getfa(fa[x]);}
signed main(){
n=read();m=read();k=read();
forup(i,1,n-1){
int u=read(),v=read();
e[u].push_back(mkp(v,i));
e[v].push_back(mkp(u,i));
}
forup(i,1,m){
int st=read(),ed=read();
dfs(st,0,i,ed);
}
forup(msk,0,(1<<m)-1){
int pp=ppcnt(msk),ff=(pp&1?-1:1),cnt=0;
forup(i,1,n-1){
fa[i]=i;
}
forup(i,1,m){
if(msk&(1<<(i-1))){
int pre=0;
for(auto j:pa[i]){
if(pre!=0) fa[getfa(j)]=getfa(pre);
pre=j;
}
}
}
forup(i,1,n-1){
if(fa[i]==i) ++cnt;
}
ans=(ans+mod+1ll*ff*ksm(k,cnt)%mod)%mod;
}
printf("%d\n",ans);
}
T4
题意就是让你求有多少个权值连续段在网格上恰好是一个矩形。
那么可以考虑扫描线,求出每个权值右端点有多少个合法的权值左端点。
但是每个点对于矩形的影响是很难做的,因为包含一个点的矩形总数量是很庞大的。怎么办呢,考虑把一个“矩形”的条件拆成更小的条件。
这里有个套路。假如你以每个格子为左上角框一个 $2\times 2$ 的小方格(包括左边缘往外一层和上边缘往外一层),容易发现网格图上有且仅有一个矩形,当且仅当恰好有 $4$ 个格子内有一个有效点,且没有任何一个格子内有三个有效点,证明考虑分讨,略。为方便叙述,我们令里面有 $k$ 个有效点的矩形个数为 $c_k$。那么容易发现,一个区间何方当且仅当区间内 $c_1+c_3=4$,因为若区间非空 $c_1$ 至少就是 $4$,然后 $c_3$ 显然不可能变成负数。
那么怎么维护呢?假如我们现在点的权值是 $x$,就有 $4$ 个小方格包含它,分别做即可。考虑对一个小方格应该怎么做。那么我们假设这个小方格里的四个数分别是 $a,b,c,x$,并且 $a<b<c<x$。画一条数轴:
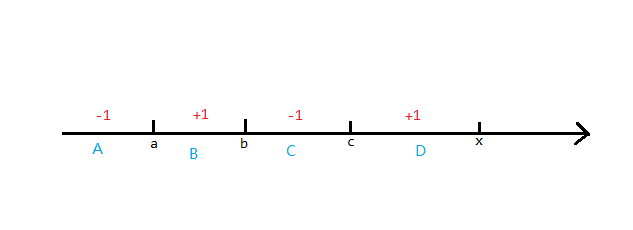
容易发现右端点为 $x$,左端点在 $D$ 区间内的的区间 $c_0-1,c_1+1$,$C$ 区间内 $c_1-1,c_2+1$,前面两个区间同理,那么就是 $B,D$ 区间的 $c_1+c_3$ 增加,其余两个减少。
这个是可以线段树维护的,要维护区间最小值和区间最小值个数。查询的时候若区间最小值为 $4$ 就产生贡献,否则不产生贡献,代码还是挺好写的。
复杂度 $O(nm\log nm)$。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(i64 i=(s);i<=(e);i++)
#define fordown(i,s,e) for(i64 i=(s);i>=(e);i--)
using namespace std;
using i64=long long;
#define gc getchar()
inline i64 read(){
i64 x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const i64 N=2e5+5,inf=0x3f3f3f3f;
i64 n,m,x[N],y[N],ans;
struct SegTree{
#define mid ((l+r)>>1)
#define lson l,mid,id<<1
#define rson mid+1,r,id<<1|1
i64 querymin[N<<2],querycnt[N<<2],mark[N<<2];
void PushUp(i64 id){
querymin[id]=min(querymin[id<<1],querymin[id<<1|1]);
querycnt[id]=0;
if(querymin[id]==querymin[id<<1]) querycnt[id]+=querycnt[id<<1];
if(querymin[id]==querymin[id<<1|1]) querycnt[id]+=querycnt[id<<1|1];
}
void PushDown(i64 id){
mark[id<<1]+=mark[id];
mark[id<<1|1]+=mark[id];
querymin[id<<1]+=mark[id];
querymin[id<<1|1]+=mark[id];
mark[id]=0;
}
void Build(i64 l=1,i64 r=n*m,i64 id=1){
if(l==r){
querycnt[id]=1;
return;
}
Build(lson);Build(rson);
PushUp(id);
}
void Update(i64 L,i64 R,i64 X,i64 l=1,i64 r=n*m,i64 id=1){
if(L<=l&&r<=R){
querymin[id]+=X;
mark[id]+=X;
return;
}
if(mark[id]) PushDown(id);
if(L<=mid) Update(L,R,X,lson);
if(mid< R) Update(L,R,X,rson);
PushUp(id);
}
i64 Ask(i64 L,i64 R,i64 l=1,i64 r=n*m,i64 id=1){
if(L<=l&&r<=R){
return querymin[id]==4?querycnt[id]:0;
}
if(mark[id]) PushDown(id);
i64 res=0;
if(L<=mid) res+=Ask(L,R,lson);
if(mid< R) res+=Ask(L,R,rson);
return res;
}
}mt;
signed main(){
n=read(),m=read();
vector<vector<i64> > a(n+5,vector<i64>(m+5));
forup(i,1,n){
forup(j,1,m){
a[i][j]=read();
x[a[i][j]]=i;y[a[i][j]]=j;
}
}
mt.Build();
forup(i,1,n*m){
vector<i64> v[4];
i64 xx=x[i],yy=y[i];
v[0].push_back(a[xx][yy]);v[0].push_back(a[xx-1][yy]);v[0].push_back(a[xx][yy-1]);v[0].push_back(a[xx-1][yy-1]);
v[1].push_back(a[xx][yy]);v[1].push_back(a[xx-1][yy]);v[1].push_back(a[xx][yy+1]);v[1].push_back(a[xx-1][yy+1]);
v[2].push_back(a[xx][yy]);v[2].push_back(a[xx+1][yy]);v[2].push_back(a[xx][yy-1]);v[2].push_back(a[xx+1][yy-1]);
v[3].push_back(a[xx][yy]);v[3].push_back(a[xx+1][yy]);v[3].push_back(a[xx][yy+1]);v[3].push_back(a[xx+1][yy+1]);
forup(j,0,3){
sort(v[j].begin(),v[j].end());
i64 nw=lower_bound(v[j].begin(),v[j].end(),i)-v[j].begin();
i64 p=0;while(v[j][p]==0) ++p;
if(nw==p){
mt.Update(1,v[j][nw],1);
}else if(nw==p+1){
mt.Update(1,v[j][nw-1],-1);
mt.Update(v[j][nw-1]+1,v[j][nw],1);
}else if(nw==p+2){
mt.Update(1,v[j][nw-2],1);
mt.Update(v[j][nw-2]+1,v[j][nw-1],-1);
mt.Update(v[j][nw-1]+1,v[j][nw],1);
}else{
mt.Update(1,v[j][nw-3],-1);
mt.Update(v[j][nw-3]+1,v[j][nw-2],1);
mt.Update(v[j][nw-2]+1,v[j][nw-1],-1);
mt.Update(v[j][nw-1]+1,v[j][nw],1);
}
}
ans+=mt.Ask(1,i);
}
printf("%lld\n",ans);
}