20231024 B 组模拟赛 题解

前言

这道题 T1 赛后大家想出一个神逼错误做法，贼好笑，我要分享给全世界。

密码是通用密码

T1

首先，这道题做法比较符合直觉。为方便叙述，设当前小王手上有 $x$ 块钱。

考虑若 $2x<B$，那么为了赢你至少要先达到 $2x$，如果你把 $x$ 分成 $t$ 份那么（在这一步）赢的概率就是 $p^t$，显然最优决策是分成一份全投进去。

但是若 $2x\ge B$，类似的，最优决策也是一份投进去，那么显然投完是不好的，只需要投 $B-x$ 即可。

那么假如你把每个 $x$ 和可能的下一个 $x$ 连有向边，那么除去连向 $0$ 和 $B$ 的边之外（因为这两个状态的值是已知的，可以直接计算出来），出度全为 $1$，也就是说它是一个内向基环森林的形式。考虑对于一个环如何算答案，容易发现如果你沿着一个环走完整的一圈，那么你会得到一个 $x=kx+b$ 的形式，直接解方程即可（就省去了高斯消元）。

复杂度 $O(B\log B)$（因为要算逆元，说不定可以去掉，另外这个上界比较松，说不定有更紧的上界）。

参考代码

#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
    int x=0,f=1;char c;
    while(!isdigit(c=gc)) if(c=='-') f=-1;
    while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
    return x*f;
}
#undef gc
const int N=1e6+5,mod=998244353;
int a,b,q,p,vis[N],ans[N];
int ksm(int a,int b){
    int c=1;
    while(b){
        if(b&1) c=1ll*a*c%mod;
        a=1ll*a*a%mod;
        b>>=1;
    }
    return c;
}
void dfs(int t,int x,int &k,int &d){
    if(t==x) return;
    if(t*2<b){
        dfs(t*2,x,k,d);
        k=1ll*k*p%mod;
        d=1ll*d*p%mod;
    }else{
        dfs(t*2-b,x,k,d);
        k=1ll*k*q%mod;
        d=(1ll*d*q%mod+p)%mod;
    }
}
int solve(int x){
    if(x==0) return 0;
    if(ans[x]) return ans[x];
    if(vis[x]){
        int k=1,d=0;
        if(x*2<b){
            dfs(x*2,x,k,d);
            k=1ll*k*p%mod;
            d=1ll*d*p%mod;
        }else{
            dfs(x*2-b,x,k,d);
            k=1ll*k*q%mod;
            d=(1ll*d*q%mod+p)%mod;
        }
        ans[x]=1ll*d*ksm(mod+1-k,mod-2)%mod;
        return ans[x];
    }
    vis[x]=1;
    if(x*2<b){
        ans[x]=1ll*p*solve(x*2)%mod;
    }else{
        ans[x]=(1ll*q*solve(x*2-b)%mod+p)%mod;
    }
    return ans[x];
}
signed main(){
    a=read(),b=read(),q=read();
    p=1ll*q*ksm(1000000,mod-2)%mod;q=(mod+1-p)%mod;
    ans[b]=1;ans[0]=0;
    printf("%d\n",solve(a));
    return 0;
}

另外我们的神逼做法是这样的：

假如你每次只拿一半的钱，你就永远不会输。

那么最终状态显然只有赢和输两种，只要你一直不输，你就一定会赢。所以答案是 $1$。

当然这是错的。

T2

我赛时唯一做出来的题。

首先考虑这个保证 $p_x=y$ 或 $p_y=x$ 的条件。容易发现它等价于在置换环上 $x,y$ 之间必须连一条有向边。那么这时候就能判无解了，即有某个点度数大于 $2$，因为置换环上每个点出度入度都必须为 $1$（算上自环）。

那么现在的问题就是你有一些游离的入度和出度需要匹配，然后每条链和环有两个方向，那直接一个阶乘乘上 $2$ 的多少次方就搞定了。

但是有个问题，就是形如这样的东西：

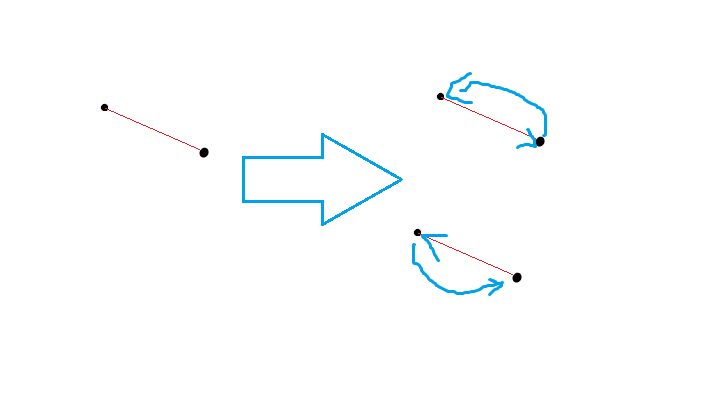
容易发现右边两种情况本质是相同的，但是会被算两次，怎么办呢？

其实这就是一个简单的容斥，大概是钦定偶数组只有一种连法的方案数减去钦定奇数组只有一种连法的方案数，具体式子很好推，不展开讲了。

复杂度 $O(n)$。

参考代码

#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
using pii=pair<int,int>;
#define fi first
#define se second
#define mkp make_pair
#define gc getchar()
inline int read(){
    int x=0,f=1;char c;
    while(!isdigit(c=gc)) if(c=='-') f=-1;
    while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
    return x*f;
}
#undef gc
const int N=5e5+5,inf=0x3f3f3f3f,mod=998244353,inv2=499122177;
int n,m,ans=1;
int ksm(int a,int b){
    int c=1;
    while(b){
        if(b&1) c=1ll*a*c%mod;
        a=1ll*a*a%mod;
        b>>=1;
    }
    return c;
}
vector<pii> adm;
vector<int> e[N];
int deg[N],vis[N];
int dfs(int x){
    vis[x]=1;
    int res=1;
    for(auto i:e[x]){
        if(vis[i]) continue;
        res+=dfs(i);
    }
    return res;
}
int fact[N],finv[N];
int C(int n,int m){
    if(n<m) return 0;
    return 1ll*fact[n]*finv[m]%mod*finv[n-m]%mod;
}
signed main(){
    n=read();m=read();
    forup(i,1,m){
        int x=read(),y=read();
        if(x>y) swap(x,y);
        adm.push_back(mkp(x,y));
    }
    sort(adm.begin(),adm.end());
    adm.erase(unique(adm.begin(),adm.end()),adm.end());
    for(auto i:adm){
        int u=i.fi,v=i.se;
        e[u].push_back(v);
        e[v].push_back(u);
        ++deg[u];++deg[v];
        if(deg[u]>2||deg[v]>2){
            puts("0");
            return 0;
        }
    }
    int cnt=n,c1=0,c2=1;
    forup(i,1,n){
        if(!vis[i]&&deg[i]==1){
            c2=2ll*c2%mod;
            int rr=dfs(i);
            if(rr==2) ++c1;
            cnt-=(rr-1);
        }
    }
    forup(i,1,n){
        if(!vis[i]&&deg[i]==2){
            int rr=dfs(i);
            if(rr>1) c2=2ll*c2%mod;
            cnt-=rr;
        }
    }
    fact[0]=1;
    forup(i,1,cnt) fact[i]=1ll*fact[i-1]*i%mod;
    finv[cnt]=ksm(fact[cnt],mod-2);
    fordown(i,cnt-1,0) finv[i]=1ll*finv[i+1]*(i+1)%mod;
    ans=1ll*c2*fact[cnt]%mod;
    forup(i,1,c1){
        c2=1ll*inv2*c2%mod;
        ans=(ans+mod+(i%2==1?-1ll:1ll)*fact[cnt-i]*C(c1,i)%mod*c2%mod)%mod;
    }
    printf("%d\n",ans);
}

T3

首先，容易发现如果你想以最小代价把书搬完，那么每个点作为搬书区间左端点/右端点的次数是很好求的。那么这个问题其实就和最优化没什么关系了。

然后考虑怎么用线段树维护询问，其实爆简单。若左儿子右端点与右儿子左端点颜色不同，新区间代价就是两边简单相加。否则就把尽量多左儿子的后缀与右儿子的前缀合并，减去 $\min(a_{mid},a_{mid+1})\times(w_{mid}+w_{mid+1})$。然后就可以直接维护了，比较简单（但是我赛时脑子抽了）。

为了维护区间涂色，还要额外维护一个“如果区间是同一个颜色，答案是多少”。

复杂度 $O(n\log n)$。

参考代码

#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(i64 i=(s);i<=(e);i++)
#define fordown(i,s,e) for(i64 i=(s);i>=(e);i--)
using namespace std;
using i64=__int128;
#define gc getchar()
i64 read(){
    i64 x=0,f=1;char c;
    while(!isdigit(c=gc)) if(c=='-') f=-1;
    while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
    return x*f;
}
void print(i64 x,i64 p=0){
    if(x==0){
        if(p==0) putchar('0');
        return;
    }
    print(x/10,p+1);
    putchar(x%10+'0');
}
const i64 N=2e5+5;
i64 n,m;
struct Info{
    i64 al,ar,wl,wr,cl,cr,val,pval;
}s[N];
Info operator +(const Info ls,const Info rs){
    Info res;
    res.al=ls.al;res.ar=rs.ar;
    res.wl=ls.wl;res.wr=rs.wr;
    res.cl=ls.cl;res.cr=rs.cr;
    res.val=ls.val+rs.val;
    if(ls.cr==rs.cl) res.val-=(ls.wr+rs.wl)*min(ls.ar,rs.al);
    res.pval=ls.pval+rs.pval;
    res.pval-=(ls.wr+rs.wl)*min(ls.ar,rs.al);
    return res;
}
struct SegTree{
    #define mid ((l+r)>>1)
    #define lson l,mid,id<<1
    #define rson mid+1,r,id<<1|1
    Info queryinfo[N<<2];
    i64 cmark[N<<2];
    void PushDown(i64 id){
        queryinfo[id<<1].cl=queryinfo[id<<1].cr=queryinfo[id<<1|1].cl=queryinfo[id<<1|1].cr=cmark[id];
        cmark[id<<1]=cmark[id<<1|1]=cmark[id];
        queryinfo[id<<1].val=queryinfo[id<<1].pval;
        queryinfo[id<<1|1].val=queryinfo[id<<1|1].pval;
        cmark[id]=0;
    }
    void Build(i64 l=1,i64 r=n,i64 id=1){
        if(l==r){
            queryinfo[id]=s[l];
            return;
        }
        Build(lson);Build(rson);
        queryinfo[id]=queryinfo[id<<1]+queryinfo[id<<1|1];
    }
    void Update1(i64 P,i64 A,i64 W,i64 l=1,i64 r=n,i64 id=1){
        if(l==r){
            queryinfo[id].al=queryinfo[id].ar=A;
            queryinfo[id].wl=queryinfo[id].wr=W;
            queryinfo[id].val=queryinfo[id].pval=W*A*2;
            return;
        }
        if(cmark[id]) PushDown(id);
        if(P<=mid) Update1(P,A,W,lson);
        else       Update1(P,A,W,rson);
        queryinfo[id]=queryinfo[id<<1]+queryinfo[id<<1|1];
    }
    void Update2(i64 L,i64 R,i64 C,i64 l=1,i64 r=n,i64 id=1){
        if(L<=l&&r<=R){
            queryinfo[id].cl=queryinfo[id].cr=C;
            cmark[id]=C;
            queryinfo[id].val=queryinfo[id].pval;
            return;
        }
        if(cmark[id]) PushDown(id);
        if(L<=mid) Update2(L,R,C,lson);
        if(mid< R) Update2(L,R,C,rson);
        queryinfo[id]=queryinfo[id<<1]+queryinfo[id<<1|1];
    }
    Info Query(i64 L,i64 R,i64 l=1,i64 r=n,i64 id=1){
        if(L<=l&&r<=R){
            return queryinfo[id];
        }
        if(cmark[id]) PushDown(id);
        Info res;
        if(R<=mid) res=Query(L,R,lson);
        else if(mid<L) res=Query(L,R,rson);
        else res=Query(L,R,lson)+Query(L,R,rson);
        return res;
    }
}mt;
signed main(){
    n=read();m=read();
    forup(i,1,n){
        i64 a=read(),c=read(),w=read();
        s[i].al=s[i].ar=a;
        s[i].cl=s[i].cr=c;
        s[i].wl=s[i].wr=w;
        s[i].val=s[i].pval=a*w*2;
    }
    mt.Build();
    forup(Case,1,m){
        i64 op=read();
        if(op==1){
            i64 x=read(),a=read(),w=read();
            mt.Update1(x,a,w);
        }else if(op==2){
            i64 l=read(),r=read(),c=read();
            mt.Update2(l,r,c);
        }else{
            i64 l=read(),r=read();
            Info res=mt.Query(l,r);
            print(res.val);
            puts("");
        }
    }
}

T4

最小割建模，赛时做不出来情有可原，NOIP 后要多看看网络流建模技巧了。

考虑问题的转化。发现题目上有一个“替换后，$C,D$ 都是 $n$ 阶排列”的条件，这其实就相当于你一次替换必须替换整个置换环。也就是说这是个决策是否替换某个置换环的问题，貌似是经典最小割建模的设问类型。

为方便叙述，记 $x_i$ 表示 $A_i$ 所在置换环是否被替换，$y_i$ 表示 $B_i$ 所在置换环是否被替换。分情况讨论一下每个 $i$ 何时会做贡献。

1. $A_i=i,B_i=i$：无论如何都会产生贡献，直接统计答案，不加入网络流图。
2. $A_i\ne i,B_i=i$：当 $x_i=0$ 时会产生贡献。
3. $A_i=i,B_i\ne i$：同理。
4. $A_i\ne i,B_i\ne i,A_i\ne B_i$：在 $x_i\lor y_i$ 时不会产生贡献。
5. $A_i\ne i,B_i\ne i,A_i = B_i$：在 $x_i\oplus y_i$ 时不会产生贡献，其中 $\oplus$ 表示异或。

那么考虑如何建模。首先容易想到源点向 $A$ 中所有置换环连边，$B$ 中所有置换环向汇点连边。然后令割开后，$A$ 在 $S$ 集合中的置换环是被替换的，$B$ 在 $T$ 集合中的置换环是被替换的。

为方便叙述，记 $A_i$ 所在的置换环为 $c(A_i)$。

首先情况 $2$，容易发现会在 $S\to c(A_i)$ 被割掉后产生贡献，即使 $S\to c(A_i)$ 的容量 $+1$。情况 $3$ 同理。

然后考虑情况 $4$，容易发现它在 $c(A_i)\in T，c(B_i)\in S$ 的时候产生贡献，那么连一条 $c(B_i)\to c(A_i)$ 的边，容量为 $1$ 即可。

最后考虑最复杂的情况 $5$，他在 $c(A_i)\in T\land c(B_i)\in S$ 或 $c(A_i)\notin T\land c(B_i)\notin S$ 时产生贡献。那么连一条 $c(A_i)\to c(B_i)$ 的容量为 $1$ 的边，再连一条 $c(B_i)\to c(A_i)$ 的容量为 $1$ 的边。它们其中之一被割掉都会产生贡献。

参考代码

#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
using pii=pair<int,int>;
#define fi first
#define se second
#define mkp make_pair
#define gc getchar()
inline int read(){
    int x=0,f=1;char c;
    while(!isdigit(c=gc)) if(c=='-') f=-1;
    while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
    return x*f;
}
#undef gc
const int N=1e5+5,inf=0x3f3f3f3f;
int n,a[N],b[N],c[N],d[N],ans,visa[N],visb[N];
vector<vector<int> > va,vb;
void find(int *a,int &la,int *vis){
    int cnt=0;
    forup(i,1,n){
        if(vis[i]||a[i]==i) continue;
        int l=i;
        ++cnt;
        do{
            vis[l]=cnt;
            l=a[l];
        }while(l!=i);
        ++la;
    }
}
struct dinic{
    struct edge{
        int v,rst,nxt;
    }e[N<<3];
    int head[N<<1],cur[N<<1],dpt[N<<1],cnte=1,s,t,szn;
    void adde(int u,int v,int w){
        e[++cnte]=edge{v,w,head[u]};head[u]=cnte;
        e[++cnte]=edge{u,0,head[v]};head[v]=cnte;
    }
    bool bfs(){
        forup(i,1,szn){
            cur[i]=head[i];
            dpt[i]=-1;
        }
        queue<int> q;q.push(s);
        dpt[s]=0;
        while(q.size()){
            int u=q.front();q.pop();
            for(int i=head[u];i;i=e[i].nxt){
                if(!e[i].rst) continue;
                int v=e[i].v;
                if(dpt[v]!=-1) continue;
                dpt[v]=dpt[u]+1;
                q.push(v);
            }
        }
        return dpt[t]!=-1;
    }
    int dfs(int x,int flow){
        if(x==t||!flow) return flow;
        int res=0;
        for(int i=cur[x];i;i=e[i].nxt){
            cur[x]=i;
            int v=e[i].v;
            if(dpt[v]==dpt[x]+1){
                int gt=dfs(v,min(e[i].rst,flow-res));
                if(gt){
                    res+=gt;
                    e[i].rst-=gt;
                    e[i^1].rst+=gt;
                    if(res==flow) break;
                }
            }
        }
        return res;
    }
    int maxflow(){
        int ans=0;
        while(bfs()){
            ans+=dfs(s,inf);
        }
        return ans;
    }
}mf;
map<pii,int> mp;
signed main(){
    n=read();
    forup(i,1,n){
        a[i]=read();
    }
    forup(i,1,n){
        b[i]=read();
    }
    int la=0,lb=0; 
    find(a,la,visa);find(b,lb,visb);
    mf.s=la+lb+1;mf.t=mf.s+1;
    mf.szn=mf.t;
    forup(i,1,n){
        if(a[i]==i){
            if(b[i]==i){
                ++ans;
            }else{
                mp[mkp(la+visb[i],mf.t)]++;
            }
        }else{
            if(b[i]==i){
                mp[mkp(mf.s,visa[i])]++;
            }else if(a[i]==b[i]){
                mp[mkp(visa[i],la+visb[i])]++;
                mp[mkp(la+visb[i],visa[i])]++;
            }else{
                mp[mkp(la+visb[i],visa[i])]++;
            }
        }
    }
    for(auto i:mp){
        int u=i.fi.fi,v=i.fi.se,w=i.se;
        mf.adde(u,v,w);
    }
    printf("%d\n",ans+mf.maxflow());
}

另外这道题最影响程序运行效率的是评测机波动……

Comments