20231023 B 组模拟赛 题解
前言
这套没啥印象,只记得 T3 除了我所有人都会打 70pts 暴力/kk。
T3 是神秘构造,但是思路意外的通畅。
T4 乔安娜这道题做的贼 nb,她赛后说是 sb 题,我问他怎么做她说按 dfs 序染色即可,我问她能不能证明她说显然,太简单了不需要证明。结果事后讲题的时候高二学长纠结了半天才搞懂她是怎么想的。另外题解的证明方法非常玄妙,而且意外的好懂,所以本文中是题解证法。
T1
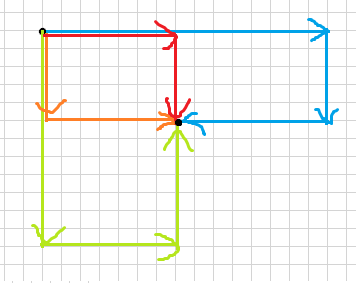
如图,容易发现路线只有四种可能,分别是从纵向的最小值绕过去,从横向的最小值绕过去和两种不绕的路线。
分类讨论即可。
复杂度 $O(n+m+q)$,瓶颈在于读入。
Success
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=2e5+5,inf=0x3f3f3f3f;
int n,m,q,a[N],b[N],ma=inf,mb=inf;
signed main(){
n=read();m=read();q=read();
forup(i,1,n) a[i]=read(),ma=min(ma,a[i]);
forup(i,1,m) b[i]=read(),mb=min(mb,b[i]);
forup(Case,1,q){
int sx=read(),sy=read(),tx=read(),ty=read();
int res=inf;
res=min(res,max({a[sx],a[tx],mb}));
res=min(res,max({b[sy],b[ty],ma}));
res=min({res,max(a[sx],b[ty]),max(b[sy],a[tx])});
if(sx==tx){
res=min(res,a[sx]);
}
if(sy==ty){
res=min(res,b[sy]);
}
printf("%d\n",res);
}
}
T2
比较简单的换根 dp 吧?
首先第一步,对于子树内的答案是好求的。设 $dp_{i,j}$ 表示考虑以 $i$ 为根的子树,$i$ 度数为 $j$,子树内其余点度数都不大于 $2$ 的连通子图个数。转移就每次 $dp_{i,k}\gets dp_{i,k-1}\times (dp_{v,0}+dp_{v,1})$ 即可($v\in son_i$,注意倒序枚举 $k$)。
然后考虑换根和求答案,首先假如当前节点是 $u$ 要换根到 $v$,那么显然要先扣掉 $dp_v$ 对 $dp_u$ 的贡献。设扣掉 $dp_v$ 贡献后的数组为 $g_i$,那么容易发现,$dp_v$ 对所有 $dp_{u,k}$ 的贡献都形如 $(dp_{v,0}+dp_{v,1})\times g_{k-1}$,而显然 $g_0$ 是已知的(显然一条边也不连的方案为 $1$ 吧),那么就可以直接推出 $g$ 了。然后的转移是简单的,和之前一样,自己推一下。
接下来考虑答案的计算,即 $\sum_{i=0}^m\sum_{j=0}^{m-i}dp_{v,i}\times g_j$,然后简单地,把内部的 $\sum$ 扔到 $g$ 那边去,就变成了 $\sum_{i=0}^mdp_{v,i}\times \sum_{j=0}^{m-i}g_j$,容易发现 $\sum_{j=0}^{m-i}g_j$ 是一个前缀和,然后就能直接维护了。
复杂度 $O(nm)$。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=3e5+5,mod=998244353;
int n,m,ans[N];
struct edge{
int v,pos;
};
vector<edge> e[N];
int dp[N][55],pd[N][55];
int ksm(int a,int b){
int c=1;
while(b){
if(b&1) c=1ll*a*c%mod;
a=1ll*a*a%mod;
b>>=1;
}
return c;
}
void dfs1(int x,int fa){
dp[x][0]=1;
for(auto i:e[x]){
if(i.v==fa) continue;
dfs1(i.v,x);
fordown(j,m,1){
(dp[x][j]+=1ll*(dp[i.v][0]+dp[i.v][1])*dp[x][j-1]%mod)%=mod;
}
}
}
int g[55];
void dfs2(int x,int fa){
for(auto i:e[x]){
if(i.v==fa) continue;
pd[i.v][0]=1;
forup(j,0,m) g[j]=pd[x][j];
forup(j,1,m){
g[j]=(g[j]+mod-1ll*(dp[i.v][0]+dp[i.v][1])*g[j-1]%mod)%mod;
}
forup(j,1,m){pd[i.v][j]=(dp[i.v][j]+1ll*dp[i.v][j-1]*(g[0]+g[1])%mod)%mod;}
int s1=1;
forup(j,1,m){
(s1+=g[j])%=mod;
}
forup(j,0,m){
(ans[i.pos]+=1ll*dp[i.v][j]*s1%mod)%=mod;
s1=(s1+mod-(g[m-j]))%mod;
}
}
for(auto i:e[x]){
if(i.v==fa) continue;
dfs2(i.v,x);
}
}
signed main(){
n=read();m=read();
forup(i,1,n-1){
int u=read(),v=read();
e[u].push_back(edge{v,i});
e[v].push_back(edge{u,i});
}
dfs1(1,0);
forup(i,0,m){
pd[1][i]=dp[1][i];
}
dfs2(1,0);
forup(i,1,n-1){
printf("%d\n",ans[i]);
}
}
T3
神秘构造题,但是思路还挺好想的。
为和直觉相符,可以把 $a,b$ 数列均 reverse 一下,就相当于前缀是 $a$,后缀是 $n\sim 1$ 的排列。
首先考虑 50pts 部分分,即序列长度不大于 $2n^2$,容易发现这道题的构造相当于要你把 $a$ 排序,但是限制你每次一个数不能前移超过一个位置,要你输出中间序列。容易发现冒泡排序是满足这个条件的,那么就可以拿到 50pts 了。但是容易发现后面的 20pts 特殊性质也能拿到,因为数据很水,而除非精心构造数据不然排完这样的数据需要的趟数是很少的。
然后就是正解,正解和部分分一点关系也没有(这是 ac 这道题的人数极少的原因之一)。首先考虑由于两个相同的数间隔不小于 $n-1$,相当于连续 $n-1$ 个数互不相同。那么可以考虑把 $b$ 序列分成 $n-1$ 个一段(先不考虑边界)。容易发现每一段内恰有一个数没出现过,不妨设上一段中这个数为 $x$,显然它在这一段是可以随意填的,还能发现每一段不会和上一段相差太大(这个比较感性,因为每个数不能往前移,即不会出现随意交换的情况)。那么可以考虑再简化问题,即对一段长度为 $n-1$ 的序列 $s$ 进行操作,并且你有一个自由的 $x$。
那么考虑你能对序列做什么,首先你可以把 $x$ 填到一个位置 $i$,那么 $s_i$ 就会变成下一段的 $x'$,相当于 swap 操作。然后你容易发现这个 $s_i$ 也能在 $i\sim n-1$ 中充当 $x$ 的作用。由于你每个数只能往后移动,换句话说,你只有 $x$ 是能自由交换的,那么显然你没有其它操作能做了。
总结下来,你的操作只有从左到右扫描 $s$,然后决策是否将当前 $x$ 与 $s_i$ 交换。
考虑如何构造决策方案,从考虑边界情况开始。容易发现若你取 $1\sim n-1$ 为第一段(注意前面说了序列是 reverse 过的),那么下一个数是固定的 $a_n$,我们无法进行操作。而你取 $2\sim n$ 为第一段,那么 $a_1$ 恰好能充当第二段的 $x$。而在最后,容易想到你需要让 $x=1$ 放到末尾,那么前面就是 $n\sim 2$ 的排列。
这里题解有个非常妙的构造,首先你可以知道最终需要使得 $s_i=n-i+1$,分两种情况。
- 若 $x=1$ 且序列 $s$ 还没排好,那么无论如何你肯定要动序列,晚动不如早动,你找到后面的第一个 $s_i\ne n-i+1$,然后交换 $x,s_i$。
- 若 $x\ne 1$,那么等到 $x=n-i+1$ 的位置就把 $x$ 给塞进去即可。
考虑这样为什么是对的,首先决策 $1$ 相当于随便找一个置换环,然后进入置换环。那么最劣情况就是耗费整整一轮才找到下一个置换环,由于数据随机,我们考虑置换环个数期望,设 $h(n)$ 表示 $n$ 阶排列置换环个数期望,考虑把 $n$ 均匀随机插入 $n-1$ 阶排列中,那么有 $\frac{1}{n}$ 的概率恰好插到 $n$ 这个位置,使置换环数量加一,其余位置不变,那么有 $h(n)=\frac{1}{n}(h(n-1)+1)+\frac{n-1}{n}h(n-1)=h(n-1)+\frac{1}{n}$,即 $h(n)=\sum_{i=1}^n\frac{1}{n}$,是一个经典的调和级数结论,大约是 $\log n$。
然后考虑对于每个 $x\ne 1$,我们的构造相当于让它前进若干步(放回原问题看了,或者你可以视为长度为 $n-1$ 的环),那么容易发现前进的步数为 $p_i-i+n[p_i<i]$。考虑求这玩意的期望,由于排列总数是好求的(就是 $n!$),那么考虑求出所有情况的总贡献,即 $\sum_{i=1}^n\sum_{j=1}^n(j-i+n[j<i])\times (n-1)!=n\times\frac{n(n-1)}{2}\times(n-1)!=n!\times\frac{n(n-1)}{2}$,然后再除以 $n!$ 就能得到期望是 $\frac{n(n-1)}{2}$。
那么 $b$ 序列期望长度就是 $(n-1)\log n+\frac{n(n-1)}{2}$,可以过了。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=1005,inf=0x3f3f3f3f;
int n,a[N],x;
vector<int> b;
int chk(){
forup(i,2,n){
if(a[i]!=n+2-i) return false;
}
return true;
}
signed main(){
n=read();
forup(i,1,n) a[i]=read();
reverse(a+1,a+n+1);
x=a[1];
forup(i,1,n) b.push_back(a[i]);
while(!chk()){
forup(i,2,n){
if(x==n+2-i||(x==1&&a[i]!=n+2-i)){
swap(a[i],x);
}
b.push_back(a[i]);
}
}
b.push_back(1);
reverse(b.begin(),b.end());
printf("%d\n",(int)b.size());
for(auto i:b){
printf("%d ",i);
}
}
T4
首先,“每个 $a_i>1$ 的边都存在一条边 $j$,使得 $i,j$ 相邻且 $a_i>a_j$”这个条件是不符合思维直觉的。考虑先把它转化成一个好想的。容易发现若从小到大加边,那么相当于每加一条边都要与之前的一条边相邻。即相当于从边 $1$ 开始,每次选一条与已染色边相邻的边染成黑色。
考虑此时如何计算代价。若在第一次涂黑以点 $u$ 为端点的边时视为把 $u$ “点亮”,把以它为端点的边全涂黑时视为把它“熄灭”,容易发现一个点的贡献就是它点亮的时间差。这时候我们就能推出来一些结论了。
首先,必定是涂完一整棵子树后才去涂其他边,因为假如一棵子树中有任何一个结点连了任何一条边,除非整棵子树都被涂完了,不然内部必定有至少一个点是点亮的状态。考虑画一画时间轴,容易发现总时间是固定的,那我们肯定希望同时点亮的点数尽可能少。
然后,我们就要考虑若已经把 $u$ 点亮了,应以什么顺序点亮它的儿子。首先由于上面的结论,那么显然子树内的答案是独立的,只需要考虑 $u$ 自己产生的贡献。那么 $u$ 产生的贡献如何计算呢?考虑在点亮最后一个儿子之前,$u$ 都是点亮的。不妨设最后一个点亮的儿子是 $v$,那么 $u$ 产生的贡献就是 $size_u-size_v$,那么显然,$v$ 取 $u$ 的重儿子最优。
综上,记 $u$ 的重儿子为 $son_u$,那么 $u$ 产生的贡献就是 $size_u-size_{son_u}$,这个就比较好计算了,可以先 dfs 一遍预处理出来(注意这个计算方式不适用于 $u$ 是叶子结点的情况)。
接下来考虑断边如何处理。首先由于我们已经把贡献化的与边无关了,那么我们完全可以把断边视作切下一棵子树 $u$,那么分四种情况讨论它到根的路径上的点 $x$ 贡献的变化。
- 本来不是叶子的变成了叶子:这个显然只有 $u$ 的父亲可能做到,贡献变成 $0$。
- 本来 $u$ 所在的儿子不是 $x$ 的重儿子:那么 $x$ 的贡献会从 $size_x-size_{son_x}$ 变成 $size_x-size_u-size_{son_x}$,即全局贡献减去 $size_{u}$。
- 本来 $u$ 所在的儿子是 $x$ 的重儿子,删了还是重儿子:贡献变成 $(size_x-size_u)-(size_{son_x}-size_u)$,即不变。
- 本来是重儿子删掉之后变成不是重儿子了:那么新的重儿子必定是次大儿子,不妨记作 $sec_x$。首先,这种情况会出现当且仅当 $size_{son_x}-size_{sec_x}<size_u$,然后贡献会从 $size_x-size_{son_x}$ 变成 $(size_x-size_u)-size_{sec_x}$,即全局贡献加上 $size_{son_x}-size_{sec_x}-size_u$。容易发现一个 $u$ 对应会产生这种贡献的 $size_{son_x}-size_{sec_x}$ 是一个前缀,那么可以用树状数组维护。
复杂度 $O(n\log n)$。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(i64 i=(s);i<=(e);i++)
#define fordown(i,s,e) for(i64 i=(s);i>=(e);i--)
using namespace std;
using i64=int;
#define gc getchar()
inline i64 read(){
i64 x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const i64 N=5e5+5;
i64 n,rt1,rt2,ans,res[N];
struct edge{
i64 u,v;
}sve[N];
vector<i64> e[N];
i64 sz[N],son[N],sec[N],f[N],sres[N],dpt[N];
void dfs1(i64 x,i64 fa){
sz[x]=1;f[x]=fa;dpt[x]=dpt[fa]+1;
for(auto i:e[x]){
if(i==fa) continue;
dfs1(i,x);
if(son[x]==0||sz[i]>=sz[son[x]]){
sec[x]=son[x];
son[x]=i;
}else if(sec[x]==0||sz[i]>sz[sec[x]]){
sec[x]=i;
}
sz[x]+=sz[i];
sres[x]+=sres[i];
}
if(son[x]){
sres[x]+=sz[x]-sz[son[x]];
}
}
struct BIT{
i64 c[N];
void upd(i64 x,i64 k){++x;for(;x<=n+1;x+=x&-x)c[x]+=k;}
i64 sum(i64 x){++x;i64 res=0;for(;x>0;x-=x&-x)res+=c[x];return res;}
}t1,t2;
void dfs2(i64 x,i64 fa,i64 cnt){
if(fa!=0){
res[x]=ans-sres[x]+t1.sum(sz[x])-(cnt+t2.sum(sz[x]))*sz[x];
if(!sec[f[x]]){
res[x]-=(sz[f[x]]-sz[x]);
}
}
if(son[x]){
if(sec[x]){
t1.upd(sz[son[x]]-sz[sec[x]],sz[son[x]]-sz[sec[x]]);
t2.upd(sz[son[x]]-sz[sec[x]],1);
dfs2(son[x],x,cnt);
t1.upd(sz[son[x]]-sz[sec[x]],-sz[son[x]]+sz[sec[x]]);
t2.upd(sz[son[x]]-sz[sec[x]],-1);
}else{
dfs2(son[x],x,cnt);
}
}
for(auto i:e[x]){
if(i==fa||i==son[x]) continue;
dfs2(i,x,cnt+1);
}
}
signed main(){
n=read();
rt1=read();rt2=read();
e[n+1].push_back(rt2);e[rt2].push_back(n+1);
e[n+1].push_back(rt1);e[rt1].push_back(n+1);
forup(i,2,n-1){
i64 u=read(),v=read();
e[u].push_back(v);
e[v].push_back(u);
sve[i]=edge{u,v};
}
dfs1(n+1,0);
ans=sres[n+1];
dfs2(n+1,0,0);
forup(i,2,n-1){
i64 u=sve[i].u,v=sve[i].v;
if(v==f[u]) swap(u,v);
printf("%d\n",res[v]-2);
}
}