20231017 B 组模拟赛 题解
前言
T4 是巨大数据结构维护 dp,暂时还没写,准备先口胡了再写。
T1
首先容易发现坏的区间是单调的。这么说比较抽象,其实是指若区间 $[l,r]$ 是坏的区间,那么它的任何超区间都是坏的(超区间指完全包含它的区间)。因为若 $[l,r]$ 中有连续的 $k$ 个那么无论怎么拓展这连续的 $k$ 个都不会变少。
那么可以维护一个双指针,每次动右指针 $R$,然后把左指针 $L$ 移到最左的合法位置,这样就有 $R-L+1$ 个好的区间。然后这个合法位置可以直接线段树维护值域,很板,就做完了。
复杂度 $O(n\log n)$(貌似可以 zkw,但是赛时没打)。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(i64 i=(s);i<=(e);i++)
#define fordown(i,s,e) for(i64 i=(s);i>=(e);i--)
using namespace std;
using i64=long long;
#define gc getchar()
inline i64 read(){
i64 x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const i64 N=2e5+5,inf=0x3f3f3f3f;
i64 n,m,a[N],ans;
i64 cnt[N];
struct SegTree{
#define mid ((l+r)>>1)
#define lson l,mid,id<<1
#define rson mid+1,r,id<<1|1
i64 querymax[N<<2],querylft[N<<2],queryrgt[N<<2];
void PushUp(i64 id,i64 len){
querymax[id]=max({querymax[id<<1],querymax[id<<1|1],queryrgt[id<<1]+querylft[id<<1|1]});
if(querymax[id<<1]==(len-(len>>1))){
querylft[id]=querymax[id<<1]+querylft[id<<1|1];
}else{
querylft[id]=querylft[id<<1];
}
if(querymax[id<<1|1]==(len>>1)){
queryrgt[id]=querymax[id<<1|1]+queryrgt[id<<1];
}else{
queryrgt[id]=queryrgt[id<<1|1];
}
}
void Update(i64 P,i64 X,i64 l=1,i64 r=n,i64 id=1){
if(l==r){
if(X==1){
querymax[id]=querylft[id]=queryrgt[id]=1;
}else{
querymax[id]=querylft[id]=queryrgt[id]=0;
}
return;
}
if(P<=mid) Update(P,X,lson);
else Update(P,X,rson);
PushUp(id,r-l+1);
}
bool Ask(){
return querymax[1]<=m;
}
}mt;
signed main(){
n=read();m=read();
forup(i,1,n){
a[i]=read();
}
i64 l=1;
forup(i,1,n){
++cnt[a[i]];
if(cnt[a[i]]==1){
mt.Update(a[i],1);
}
while(l<i&&!mt.Ask()){
--cnt[a[l]];
if(cnt[a[l]]==0){
mt.Update(a[l],0);
}
++l;
}
ans+=i-l+1;
}
printf("%lld\n",ans);
}
T2
这道题赛时傻逼了,卡住了,最后也没写出来。
首先 pop 操作的答案是简单的,从前往后扫一遍可以知道每个数从什么时候开始变得不是最大值,也就是说可能被删掉,并且容易发现 pop 操作会等概率删掉当前能被删掉但有可能没被删掉的所有数(就是说除去最大值)。对于这个“有可能没被删掉”,意思就是除去每次删到只剩最大值时会清空集合,其余时候是累加的。
然后考虑 push 操作,其实也不难。在刚才“扫一遍”的过程中,你能求出每个数从什么时候开始可能被删掉,那么直到集合删空之前的所有操作都能等概率把它删掉,那么再倒着扫一遍即可。
复杂度 $O(n)$,需要预处理逆元。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
using pii=pair<int,int>;
#define fi first
#define se second
#define mkp make_pair
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=1e6+5,mod=998244353;
int n,sum[N],mx[N],pmx[N],inv[N],ans[N],tg[N];
struct op{
int tp,val;
}s[N];
signed main(){
n=read();
inv[1]=1;
forup(i,2,n){
inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
}
forup(i,1,n){
s[i].tp=read();
if(s[i].tp==0){
s[i].val=read();
sum[i]=sum[i-1]+1;
if(s[i].val>mx[i-1]){
mx[i]=s[i].val;
pmx[i]=i;
}else{
mx[i]=mx[i-1];
pmx[i]=pmx[i-1];
}
}else{
sum[i]=sum[i-1]-1;
if(sum[i]!=0){
mx[i]=mx[i-1];
pmx[i]=pmx[i-1];
}else{
mx[i]=0;
pmx[i]=0;
}
}
}
int nw=0;
forup(i,1,n){
if(s[i].tp==0){
if(s[i].val==mx[i]){
tg[i]=pmx[i-1];
nw=(1ll*nw*(mod+1-inv[sum[i]-1])%mod+1ll*mx[i-1]*inv[sum[i]-1]%mod)%mod;
}else{
tg[i]=i;
nw=(1ll*nw*(mod+1-inv[sum[i]-1])%mod+1ll*s[i].val*inv[sum[i]-1]%mod)%mod;
}
}else{
if(sum[i]>0){
ans[i]=nw;
}else{
ans[i]=mx[i-1];
tg[i]=pmx[i-1];
nw=0;
}
}
}
nw=0;
fordown(i,n,1){
if(s[i].tp==1){
nw=(1ll*nw*(mod+1-inv[max(sum[i],1)])%mod+1ll*i*inv[max(sum[i],1)]%mod)%mod;
}
if(tg[i]!=0){
if(nw!=0){
ans[tg[i]]=nw;
}
}
}
forup(i,1,n){
printf("%d ",ans[i]);
}
}
T3
很巧妙的结论题。
首先考虑有一些操作是显然不优的,如图:
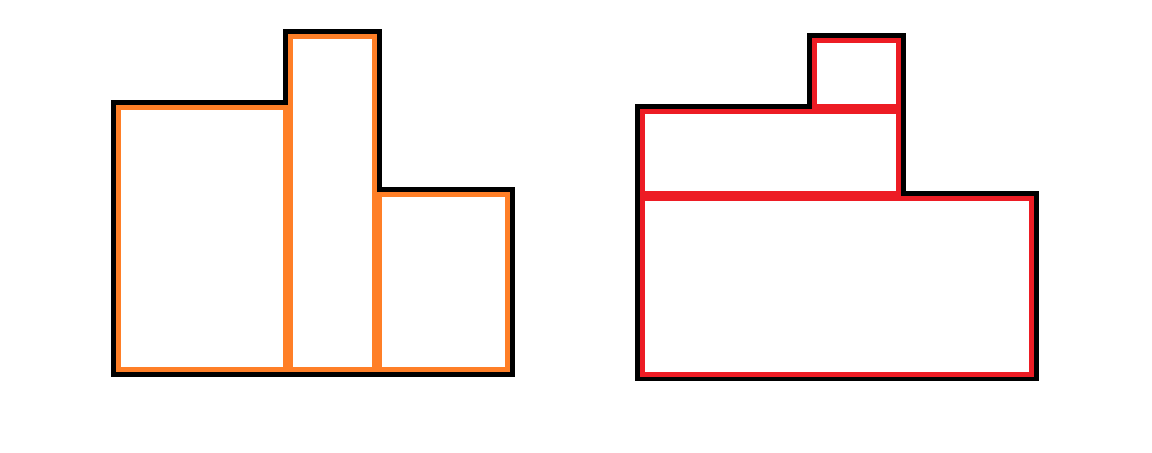
左边橙色的切法显然不如右边红色的切法(考虑权值的计算方法),举例说,左边下面大块的每一行产生了三次贡献,右边只产生了一次贡献。
这说明每一块肯定都是从左到右拉通的,但是有一种例外,就是单独一竖列的情况,因为单独一列的权值计算方式不同,这个我们要分开考虑。
那么由于我们是一层一层切的,容易想到 dp,设 $dp_{l,r,k}$ 表示考虑区间 $[l,r]$($a_l\sim a_r$ 均大于 $a_k$,不然不好转移),然后这一整个区间都被切掉了下半 $a_k$ 高度后(或者离散化后记删掉高度为 $k$ 的一块),还需要多少代价才能删完。
转移有两个,就是上面的两种情况,第一个是从左到右拉通删,那么删的高度显然必须是区间最小值(删多了不合法,删少了不优),第二个是删某一列。那么就要枚举删哪一列,复杂度为 $O(n^4)$。
但是容易发现,只有删最高的一列是不劣的,考虑画图:
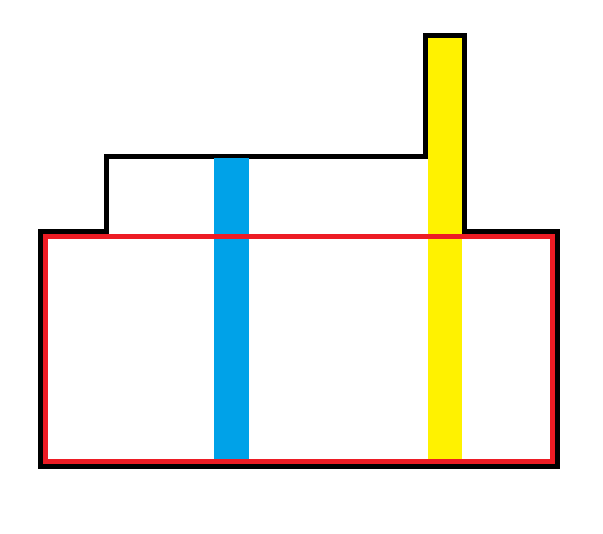
如果你删蓝色的一列,那么由于红色矩形每一行的最大值显然取在黄色的那一列里面,那么蓝色列分出的右半边权值和原来的红色矩形相同,而左半边凭空多出来了,显然是更劣的。
那么具体来说,转移有两种,设 $a_p$ 为 $[l,r]$ 内的最小值,$a_q$ 为 $[l,r]$ 内的最大值,那么两种转移分别是:
$$dp_{l,r,k}=\min(dp_{l,q-1,k}+dp_{q+1,r,k}+cost_{q,q,k,a_q},dp_{l,p-1,p}+dp_{p+1,r,p}+cost_{l,r,k,p})$$
其中 $cost_{l,r,d,u}$ 表示删掉左边缘为 $l$,右边缘为 $r$,下边缘为 $d$,上边缘为 $u$ 的矩形的代价,这个可以 $O(1)$ 计算,是一个比较简单的模拟。
那么做个 RMQ 转移就是 $O(1)$ 的,复杂度是 $O(n^3)$……
吗?
其实这个做法加个记搜就能过了,因为可以证明状态数是 $O(n^2)$ 级别的。
首先考虑你的转移,首先如果只考虑最大值的转移,那么能被转移到的 $[l,r]$ 必定是笛卡尔树上的一个子树,是 $O(n)$ 级别的(这个等会会用到),而对于一个 $k$,根据状态的定义,容易发现 $i\in[l,r]$ 的所有 $a_i$ 必定大于 $a_k$,那么相当于整个序列把 $a_i\le a_k$ 的所有 $i$ 删掉后形成的一系列子区间。对于这样形成的极大子区间 $[L,R]$ 内,容易发现合法的 $l,r$ 要么 $l=L$ 或 $r=R$,要么是一个当前子区间笛卡尔树的子树。对于前者,它是一个前缀或后缀,显然是 $O(n)$ 的,对于后者,刚才已经说明了是 $O(n)$ 的。又因为 $k$ 有 $O(n)$ 种取值,那么乘起来状态数就是 $O(n^2)$ 的了。
复杂度 $O(n^2\log n)$(因为你要用一个容器存状态,如果用 map 就带 $\log$,或许可以试试哈希表)。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=3005,inf=0x3f3f3f3f;
int n,a[N];
int ST1[12][N],ST2[12][N],lg[N];
void init(){
forup(i,2,n) lg[i]=lg[i>>1]+1;
forup(i,1,n) ST1[0][i]=i,ST2[0][i]=i;
forup(i,1,11){
forup(j,1,n-(1<<i)+1){
ST1[i][j]=a[ST1[i-1][j]]>a[ST1[i-1][j+(1<<(i-1))]]?ST1[i-1][j]:ST1[i-1][j+(1<<(i-1))];
ST2[i][j]=a[ST2[i-1][j]]<a[ST2[i-1][j+(1<<(i-1))]]?ST2[i-1][j]:ST2[i-1][j+(1<<(i-1))];
}
}
}
int query1(int l,int r){
int len=lg[r-l+1];
return a[ST1[len][l]]>a[ST1[len][r-(1<<len)+1]]?ST1[len][l]:ST1[len][r-(1<<len)+1];
}
int query2(int l,int r){
int len=lg[r-l+1];
return a[ST2[len][l]]<a[ST2[len][r-(1<<len)+1]]?ST2[len][l]:ST2[len][r-(1<<len)+1];
}
struct Node{
int l,r,k;
bool operator <(const Node &pp)const{
if(l!=pp.l) return l<pp.l;
if(r!=pp.r) return r<pp.r;
return a[k]<a[pp.k];
}
};
map<Node,int> dp;
int calc(int mx,int st,int ed){
int ll=mx-ed+1,rr=mx-st;
return (ll+rr)*(rr-ll+1)/2;
}
int solve(int l,int r,int k){
if(l>r) return 0;
if(l==r){return a[l]-a[k];}
if(dp.count(Node{l,r,k})) return dp[Node{l,r,k}];
int res=inf;
int mx=query1(l,r),mn=query2(l,r);
res=min(solve(l,mx-1,k)+solve(mx,mx,k)+solve(mx+1,r,k),solve(l,mn-1,mn)+solve(mn+1,r,mn)+calc(a[mx],a[k],a[mn]));
dp[Node{l,r,k}]=res;
return res;
}
signed main(){
n=read();
forup(i,1,n) a[i]=read();
init();
printf("%d\n",solve(1,n,0));
}
T4
这道题貌似是道比较板的 dp of dp。
首先恰好有奇数个有恰好奇数个本质不同子序列的非空子串的方案数这个很复杂,不妨先想对于固定字符串有恰好奇数个本质不同子序列这么一个子问题。
那么容易想到 dp,设 $g_{i,0/1/2}$ 表示考虑前 $i$ 个数,恰好有多少个以 $0/1/2$ 结尾的本质不同子序列有多少种,但是为了方便转移我们还可以记一个 $g_{i,3}$ 表示本质不同序列总数(包括空序列)。那么考虑转移,假如已经确定了第 $i$ 位是多少,那么不妨以 $0$ 为例,则 $g_{i,0}=g_{i-1,0}+g_{i-1,1}+g_{i-1,2}+1=g_{i-1,3}$,因为你这个 $0$ 可以接在任何原来的子序列后面,然后 $g_{i,1/2}$ 都可以直接继承,新的 $g_{i,3}=g_{i,0}+g_{i,1}+g_{i,2}+1=g_{i-1,3}+g_{i-1,1}+g_{i-1,2}+1$。至于为什么 $g_{i,0}$ 不需要继承 $g_{i-1,0}$,考虑这么一种情况:
容易发现,对于第一个 $0$ 的 $7$ 个本质不同子序列 0,10,20,120,210,110,1210,在第二个 $0$ 都能从 $g_{i-1,1}$ 和 $g_{i-1,2}$(以及空序列)转移过来,如果继承了会算重。
那么我们就能求出一子串有多少个本质不同的子序列了。但容易发现这太浪费了,因为我们只关注子序列个数的奇偶性。考虑把 dp 的值设成 bool 型的,观察一下每个 dp 状态的奇偶性有什么性质。
为方便叙述,把 $g_{i,0/1/2/3}$ 写成一个向量 $\begin{bmatrix}g_0,g_1,g_2,g_3\end{bmatrix}$,那么初始状态就是 $\begin{bmatrix}0,0,0,1\end{bmatrix}$,假如 $s_i=0$,就会转移到 $\begin{bmatrix}1,0,0,0\end{bmatrix}$,而假如 $s_i=1$ 就是 $\begin{bmatrix}0,1,0,0\end{bmatrix}$,容易发现这相当于交换 $g_{s_i}$ 与 $g_3$。
那么这对于初始情况以外的情况是否适用呢?这个我们可以只看前两步,对于第一次转移显然,对于第二次,若 $g_3=g_{s_i}=0$,容易发现 $g_3$ 转移过后仍是 $0$,$g_{s_i}$ 也是,若 $g_3=0,g_{s_i}=1$,那么转移过后 $g_3=1,g_{s_i}=0$。而再进一步地,可以发现后面的所有情况均在前两次转移中可以出现。
也就是说本质不同的状态只有四种,分别是 $\begin{bmatrix}1,0,0,0\end{bmatrix},\begin{bmatrix}0,1,0,0\end{bmatrix},\begin{bmatrix}0,0,1,0\end{bmatrix},\begin{bmatrix}0,0,0,1\end{bmatrix}$,不妨设 $p_0=\begin{bmatrix}1,0,0,0\end{bmatrix},p_1=\begin{bmatrix}0,1,0,0\end{bmatrix},p_2=\begin{bmatrix}0,0,1,0\end{bmatrix},p_3=\begin{bmatrix}0,0,0,1\end{bmatrix}$。
这时候容易发现对于非固定字符串变得好处理了,这个具体为什么语言不太好描述,画一张图:
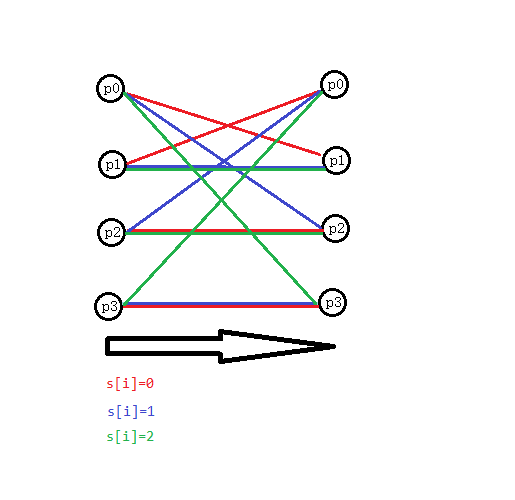
那么显然对于一个固定的 $s_i$ 转移是固定的,那么我们就可以设 $dp_{i,0/1/2/3}$ 表示考虑前 $i$ 个,$g_i=p_0/p_1/p_2/p_3$ 的填数方案数,然后对于一个可变的数那几种转移全转一遍即可,这样就能处理对于一不固定字符串使其恰好有奇数个本质不同子序列的填数方案了(虽然这个和解题关系不大)。
那么再考虑外层的有奇数个满足以上条件子串如何处理(先不考虑区间询问),那么因为维护的是子区间,那么不妨对于每个点维护以它为右端点的后缀的方案数再累加,而且我们同样不关心具体是多少,只关心奇偶性,那么容易想到设 $f_{i,0/1,0/1,0/1,0/1,0/1}$ 表示考虑前 $i$ 个数,有偶数/奇数个后缀的状态是 $p_0$,有偶数/奇数个后缀的状态是 $p_1$,有偶数/奇数个后缀的状态是 $p_2$,有偶数/奇数个后缀的状态是 $p_3$,$i$ 之前好的非空子串数量是偶数/奇数的填数方案(好长的状态定义)。
根据刚才图上的转移,容易发现 $f$ 的转移也是一个交换的过程,即交换 $p_0$ 与 $p_{s_i+1}$,对于最后一维的答案统计,相当于每次累加上 $p_0$。另外注意,$i$ 后移时还会新增一个状态为 $p_0$ 的空串。形式化的,以 $s_i=0$ 举例:
$$f_{i,a_3,a_1,a_2,a_0\oplus 1,a_4\oplus a_0}\gets f_{i-1,a_0,a_1,a_2,a_3,a_4}$$
其中 $\oplus$ 表示异或(显然二进制不进位加法就是异或吧)。
然后和之前的 $dp$ 数组的转移一样,对于可变的位置同时进行多种转移。
那么考虑区间询问。首先容易想到把转移封装进矩阵后用线段树维护,那么复杂度就是 $O(n\times s^3 + q\log n\times s^3)$($s$ 为状态数,这里取 $32$),$50000\times 32^3+1000000\times \log_2 50000\times 32^3\approx 5.2\times 10^{11}$,显然过不了。
首先有个显而易见的优化,由于你只关心每个状态是多少,那么你线段树最终查询合并 $\log n$ 个区间的时候其实只需要上传一个行向量,那么查询时向量乘矩阵的乘法就变成 $O(s^2)$ 的了。总复杂度 $O(n\times s^3+q\log n\times s^2)$,还是不太过得了。
继续优化,容易发现对于一个 $s_i=0/1/2$,转移的矩阵大部分是空的,因为显然对于一个状态 $\begin{bmatrix}a_0,a_1,a_2,a_3,a_4\end{bmatrix}$,它只会转移到 $\begin{bmatrix}a_1\oplus 1,a_0,a_2,a_3,a_4\oplus a_1\end{bmatrix}$,也就是说,转移矩阵每一行只有一个位置有值。就算对于 $s_i=\text{?}$ 这种阴间情况也只有至多 $3n$ 个转移,反正就是 $O(n)$ 的。这样的矩阵也是可以 $O(s^2)$ 和一般矩阵做乘法的,就是先枚举这边有哪些地方有值,然后有值才乘以对应的一行/一列。我们可以考虑用猫树维护,这样查询的时候压掉一个 $\log$,预处理的时候还能变成 $O(s^2)$ 的矩乘,复杂度就变成了 $O(n\log n\times s^2+qs^2)$(注意查询是做两遍向量乘矩阵,一定要尽量避免矩阵乘矩阵)。
但是直接猫树空间要炸,打猫树分治就没问题了,复杂度还是一样。
然后还有一个优化,由于每次 $i$ 增加时,$a_0,a_1,a_2,a_3$ 四个数都会在交换之后对其中一个异或 $1$,也就是说这四个数的异或和只与 $i-l$($l$ 是查询区间左端点)有关,那么在状态中我们只需要记三个值,然后再讨论奇偶性分开记一个 $f'$,这样矩阵乘法中的 $s$ 就会从 $32$ 变成 $16$,然后提一个 $2$ 出来放在外面,效率还能提升一倍,但是需要对奇数$\to$ 偶数,偶数 $\to$ 奇数构造两种转移矩阵。
看起来代码很难写,实际上确实很难写。
过了,很卡常,有个卡常技巧是最后你其实也不需要乘一整个向量。初始向量只有一个地方有值($v_0=1$),你可以左边矩阵枚举对应的一行,然后假如有值再去乘右边矩阵对应的一行,复杂度上界没变,但是很多时候常数会减小。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=5e4+5,M=1e6+5,mod=998244353;
int t,n,seq[N],m,ans[M];
struct Matrix{
int c[16][16];
bool is_sparse;
Matrix(){
mem(c,0);is_sparse=false;
}
};
Matrix tran[2][7];//0,1,2,a,b,c,?
void adm(int &a,int b){
a+=b;
if(a>=mod) a-=mod;
}
Matrix operator *(const Matrix &a,const Matrix &b){
Matrix res;
if(b.is_sparse){
forup(j,0,15){
forup(k,0,15){
if(b.c[k][j]){
forup(i,0,15){
adm(res.c[i][j],1ll*a.c[i][k]*b.c[k][j]%mod);
}
}
}
}
}else if(a.is_sparse){
forup(i,0,15){
forup(k,0,15){
if(a.c[i][k]){
forup(j,0,15){
adm(res.c[i][j],1ll*a.c[i][k]*b.c[k][j]%mod);
}
}
}
}
}else{
puts("Genshin");
exit(0);
}
return res;
}
Matrix operator +(const Matrix &a,const Matrix &b){
Matrix res;
forup(i,0,15){
forup(j,0,15){
res.c[i][j]=a.c[i][j];
adm(res.c[i][j],b.c[i][j]);
}
}
return res;
}
char str[N];
int gmsk(int *a){
int res=0;
res=(a[0]|(a[1]<<1)|(a[2]<<2)|(a[4]<<3));
return res;
}
void init(){
forup(msk,0,15){
int a[5],b[5];
a[0]=msk&1;a[1]=(msk>>1)&1;a[2]=(msk>>2)&1;a[4]=(msk>>3)&1;
int p=a[0]^a[1]^a[2];
forup(xs,0,1){
a[3]=xs^p;
forup(s,0,2){
forup(i,0,4) b[i]=a[i];
swap(b[s],b[3]);
b[4]^=b[3];
b[3]^=1;
int mb=gmsk(b);
tran[xs][s].c[msk][mb]++;
}
}
}
forup(xs,0,1){
tran[xs][3]=tran[xs][0]+tran[xs][1];
tran[xs][4]=tran[xs][0]+tran[xs][2];
tran[xs][5]=tran[xs][1]+tran[xs][2];
tran[xs][6]=tran[xs][0]+tran[xs][1]+tran[xs][2];
}
forup(xs,0,1){
forup(i,0,6){
tran[xs][i].is_sparse=true;
}
}
}
struct query{
int l,r;
}q[M];
Matrix ns[N][2];
vector<int> sv[1<<17];
int grt(int l,int r){
l+=(1<<16);r+=(1<<16);
while(l^r){l>>=1;r>>=1;}
return l;
}
void solve(int sl,int sr,int id){
if(sl==sr){
if(sv[id].empty()) return;
int res=0;
forup(i,0,7){
(res+=tran[1][seq[sl]].c[0][i|8])%=mod;
}
for(auto i:sv[id]){
ans[i]=res;
}
return;
}
int mid=(sl+sr)>>1;
if(sv[id].size()){
ns[mid][0]=tran[1][seq[mid]];ns[mid][1]=tran[0][seq[mid]];
ns[mid+1][0]=tran[1][seq[mid+1]];ns[mid+1][1]=tran[0][seq[mid+1]];
fordown(i,mid-1,sl){
ns[i][0]=tran[1][seq[i]]*ns[i+1][1];
ns[i][1]=tran[0][seq[i]]*ns[i+1][0];
}
forup(i,mid+2,min(sr,n)){
ns[i][0]=ns[i-1][1]*tran[1][seq[i]];
ns[i][1]=ns[i-1][0]*tran[0][seq[i]];
}
for(auto i:sv[id]){
Matrix m1(ns[q[i].l][0]),m2(((q[i].r-q[i].l+1)&1)?ns[q[i].r][0]:ns[q[i].r][1]);
int res=0;
forup(i,0,15){
if(m1.c[0][i]){
forup(j,0,7){
(res+=1ll*m2.c[i][j|8]*m1.c[0][i]%mod)%=mod;
}
}
}
ans[i]=res;
}
}
solve(sl,mid,id<<1);solve(mid+1,sr,id<<1|1);
}
bool cmp(query a,query b){
return a.r<b.r;
}
signed main(){
init();
n=read();
scanf(" %s",str+1);
forup(i,1,n){
if(str[i]>='0'&&str[i]<='2') seq[i]=str[i]-'0';
else if(str[i]>='a'&&str[i]<='c') seq[i]=str[i]-'a'+3;
else seq[i]=6;
}
m=read();
forup(i,1,m){
q[i].l=read();q[i].r=read();
int ps=grt(q[i].l,q[i].r);
sv[ps].push_back(i);
}
solve(0,(1<<16)-1,1);
forup(i,1,m){
printf("%d\n",ans[i]);
}
}