20231010 B 组模拟赛 题解
前言
这场我记得 T1 没看到“保证边在交点以外的任何地⽅不相交”这句话(其实是看到了,但是没看懂这句话是啥意思),然后 T4 是原题但是赛时没写出来,记得当时好像被初三老哥薄纱了。
然后这场四道都是原题,一看就是 h 先生的模拟赛。
T1
首先可以 $O(n)$ DFS 一遍给能从东侧到达的所有点染色,然后就只关注这些染了色的点了,把其它点全删掉,下文默认所有点都能从东侧到达。
注意这句话:
保证边在结点以外的任何地⽅不相交
这是什么意思?我们画一张图:
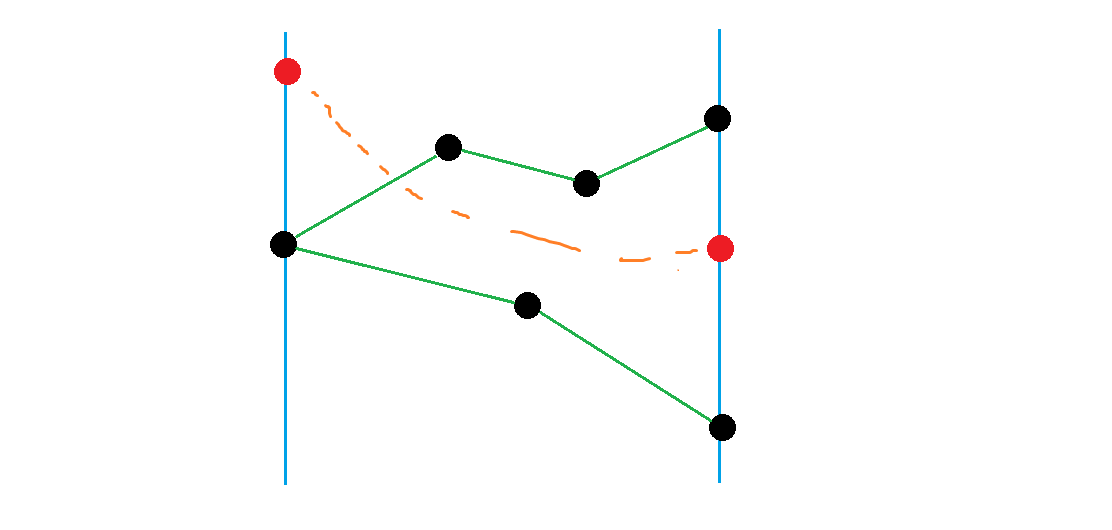
假如黑色点和绿色边是已知的,然后存在一条路径从左侧红色点连到右侧红色点(橙色虚线)。由于边不相交,这就说明橙色路径中必定不和绿色路径相交,也就是必定经过黑色点。
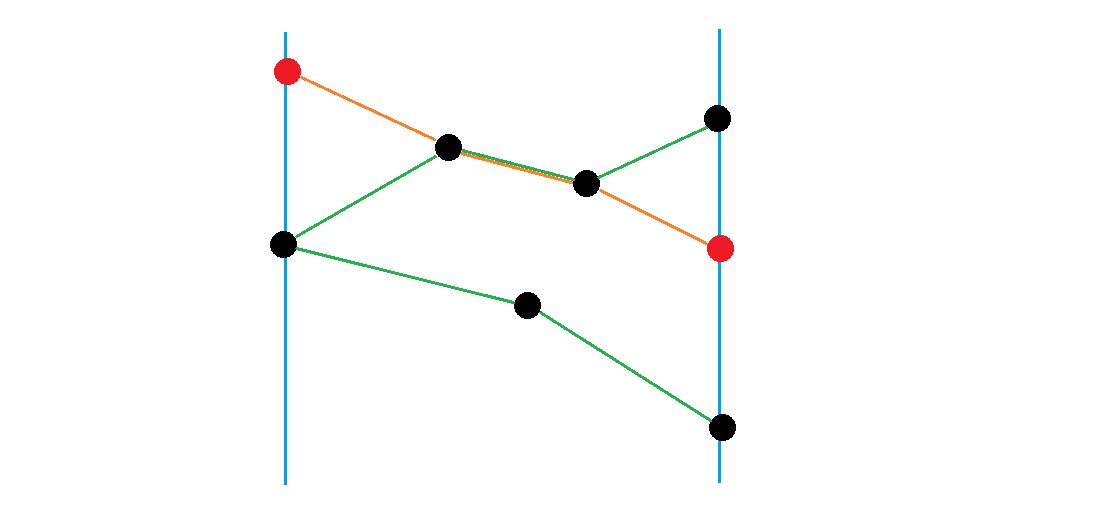
比如可能是这样的。
这说明什么?若存在两条路径 $u\to x,v\to y$ 相交,那么 $u$ 也能到达 $y$,$v$ 也能到达 $x$。那么考虑再进一步,容易发现,东侧点某个点 $u$ 必定能到达西侧的一整个连续的区间(或者无法到达西侧)。
那么就简单了,首先由于我们只关注连通性,可以缩掉强连通分量,然后就是一个 DAG 了,那么我们可以按反图的拓扑序 DP,维护每个强连通分量能到达的西侧最高点和最低点,然后把编号相减即可。具体转移很简单,不做赘述。
貌似有不用缩点的办法,但是我不太懂。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
using pii=pair<int,int>;
#define fi first
#define se second
#define mkp make_pair
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=3e5+5,inf=0x3f3f3f3f;
int dp[2][N],n,m,a,b,x[N],y[N],rd[N],ans[N];
int mp[N];
struct edge{
int u,v;
};
vector<edge> sve;
vector<int> e[N],re[N],est[N];
int dfn[N],low[N],Tm,ist[N],csc,blg[N];
stack<int> stk;
queue<int> q;
vector<pii> eseq;
int vis[N];
void dfs1(int u){
vis[u]=1;
if(x[u]==a){
eseq.push_back(mkp(y[u],u));
}
for(auto i:e[u]){
if(vis[i]) continue;
dfs1(i);
}
}
void Tarjan(int j){
low[j]=dfn[j]=++Tm;
ist[j]=1;stk.push(j);
for(auto i:e[j]){
if(!vis[i]) continue;
if(!dfn[i]){
Tarjan(i);
low[j]=min(low[j],low[i]);
}else if(ist[i]){
low[j]=min(low[j],dfn[i]);
}
}
if(dfn[j]==low[j]){
++csc;
while(stk.top()!=j){
int u=stk.top();
blg[u]=csc;
ist[u]=0;
if(x[u]==a){
dp[0][csc]=min(dp[0][csc],mp[u]);
dp[1][csc]=max(dp[1][csc],mp[u]);
}
if(x[u]==0){
est[csc].push_back(u);
}
stk.pop();
}
blg[j]=csc;
ist[j]=0;
if(x[j]==a){
dp[0][csc]=min(dp[0][csc],mp[j]);
dp[1][csc]=max(dp[1][csc],mp[j]);
}
if(x[j]==0){
est[csc].push_back(j);
}
stk.pop();
}
}
signed main(){
n=read();m=read();a=read();b=read();
mem(dp[0],0x3f);
forup(i,1,n){
x[i]=read();y[i]=read();
}
forup(i,1,m){
int u=read(),v=read(),k=read();
e[u].push_back(v);
sve.push_back(edge{u,v});
if(k==2){
e[v].push_back(u);
}
}
forup(i,1,n){
if(x[i]==0){
dfs1(i);
}
}
sort(eseq.begin(),eseq.end());
forup(i,0,eseq.size()-1){
mp[eseq[i].se]=i+1;
}
forup(i,1,n){
if(vis[i]&&!dfn[i]) Tarjan(i);
}
for(auto i:sve){
if(!vis[i.u]||!vis[i.v]) continue;
int u=blg[i.u],v=blg[i.v];
if(u==v) continue;
re[v].push_back(u);
}
forup(i,1,csc){
sort(re[i].begin(),re[i].end());
re[i].erase(unique(re[i].begin(),re[i].end()),re[i].end());
for(auto j:re[i]){
rd[j]++;
}
}
while(q.size()) q.pop();
forup(i,1,csc){
if(rd[i]==0) q.push(i);
}
while(q.size()){
int u=q.front();q.pop();
for(auto i:re[u]){
rd[i]--;
if(rd[i]==0) q.push(i);
dp[0][i]=min(dp[0][i],dp[0][u]);
dp[1][i]=max(dp[1][i],dp[1][u]);
}
}
forup(i,1,csc){
for(auto j:est[i]){
ans[j]=max(0,dp[1][i]-dp[0][i]+1);
}
}
vector<pii> res;
forup(i,1,n){
if(x[i]==0){
res.push_back(mkp(y[i],ans[i]));
}
}
sort(res.begin(),res.end(),greater<pii>());
for(auto i:res){
printf("%d\n",i.se);
}
}
T2
期望题(还是离散型的),赛时直接跳了。但貌似暴力很好打的样子,痛失暴力分。
首先注意提示中的这句话:
对于 $n$ 个 $[0,1]$ 之间的随机变量 $x_1,x_2,\dots,x_n$,第 $k$ ⼩的那个的期望值是 $\frac{k}{n+1}$。
他给这个提示肯定是有用的,容易发现我们只要求出最小生成树上最大的那条边的排名取到 $k\in[1,m]$ 的概率分别是多少,然后乘以贡献相加即可。
那么假如我们按边权从小到大加边,当整张图第一次联通的时候,正在加的这条边就会产生贡献。形象化的,把恰好加到第 $n$ 条边时整张图首次联通的概率记作 $P(x=n)$,那么答案就是 $\sum_{k=0}^m\frac{k}{m+1}P(x=k)=\frac{1}{m+1}\sum_{k=0}^mkP(x=k)$。套路地,转化为 $\frac{1}{m+1}\sum_{k+0}^mP(x>k)$,其中 $P(x>k)$ 表示加到 $k$ 条边时整张图仍不连通的概率。
由于 $n$ 很小,考虑状压,这里开始就非常巧妙了。设 $f_{i,msk}$ 表示加入了 $i$ 条边,每条边的左右端点都在 $msk$ 中,使 $msk$ 不连通的方案数,$g_{i,msk}$,表示连通的方案数。为方便叙述,设 $h(msk)$ 表示左右端点都在 $msk$ 内的边的总数,易得(?)转移方程:
$$f_{i,msk}=\sum_{S\subsetneq msk\land p\in S}\sum_{j=0}^ig_{j,S}\dbinom{h(msk-S)}{i-j}$$
其中 $p$ 是随意钦定的一个点,满足 $p\in msk$。
首先,上面的意思是把 $msk$ 分成 $S,msk-S$ 两个集合,然后钦定两个集合之间不连边,然后 $S$ 内部用 $j$ 条边连通,其余随意连边。
至于为什么要钦定一个 $p$,容易发现 $msk-S$ 是有可能连通的,如果不钦定会在 $j'=i-j$ 时将当前情况重复计算,如果钦定连通的那一半包含某个点,由于每个点必然属于其中一边,那么就会自动去掉重复的情况。而在每种情况下,钦定的 $p$ 必然属于某个连通块,而 $S$ 显然能取遍 $p$ 可能所属的所有连通块,这样就不重不漏了。
那么如何求 $g$ 呢?这其实非常简单,因为显然 $f_{i,msk}+g_{i,msk}=\dbinom{h(msk)}{i}$,$g$ 可以直接计算。于是就做完了,复杂度 $O(3^nm^2)$。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(i64 i=(s);i<=(e);i++)
#define fordown(i,s,e) for(i64 i=(s);i>=(e);i--)
using namespace std;
using i64=long long;
#define gc getchar()
inline i64 read(){
i64 x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const i64 N=10,M=55;
i64 n,m,al;
i64 sz[1<<N],f[1<<N][M],g[1<<N][M];
i64 C[M][M];
double ans;
signed main(){
n=read();m=read();
al=(1<<n)-1;
forup(i,1,m){
i64 u=read()-1,v=read()-1;
sz[(1<<u)|(1<<v)]++;
}
forup(i,0,m){
C[i][0]=1;
forup(j,1,i){
C[i][j]=C[i-1][j-1]+C[i-1][j];
}
}
forup(i,0,n-1){
forup(msk,0,al){
if(msk&(1<<i)){
sz[msk]+=sz[msk^(1<<i)];
}
}
}
forup(i,0,al){
if(i==(i&-i)){
f[i][0]=0;
g[i][0]=1;
}else{
f[i][0]=1;
g[i][0]=0;
}
}
forup(msk,1,al){
i64 p=msk&-msk;
forup(i,1,m){
if(i>sz[msk]){
g[msk][i]=f[msk][i]=0;
continue;
}
for(i64 ss=msk&(msk-1);ss;ss=(ss-1)&msk){
if(!(ss&p)) continue;
forup(j,0,i){
f[msk][i]+=g[ss][j]*C[sz[msk^ss]][i-j];
}
}
g[msk][i]=C[sz[msk]][i]-f[msk][i];
}
}
forup(i,0,m){
ans+=1.0*f[al][i]/C[m][i];
}
printf("%.6lf\n",ans/(m+1));
}
T3
挺板的数据结构题,但是赛后没看题解改出来了,中间大部分维护思路是在研学的时候想的,自己独立发明了线段树维护历史总和,感觉自己屌爆了。
首先考虑最大值怎么维护,最小值类似。
我们可以单调栈求出 $i$ 左侧最近的大于 $a_i$ 的位置 $L_i$,右侧第一个 $R_i$,那么 $i$ 在 $l\in(L_i,i],r\in [i,R_i)$ 的区间 $[l,r]$ 中会产生贡献,如果把区间按 $l$ 为纵坐标 $r$ 为横坐标放在矩阵上就是一个矩形,可以扫描线维护。
那么题意就转化成了有若干个三元组 $((x_1,y_1),(x_2,y_2),v)$,表示两点围成的矩形中所有点 $a_{i,j}$ 的权值都加 $v$,然后查询某矩形内所有点权值和。
那么可以把修改和查询都拆成两条垂直线段 $(x_1,y_1)-(x_1,y_2),(x_2,y_1)-(x_2,y_2)$,然后扫描线维护区间历史总和(即扫描到第 $i$ 列时 $v_i=\sum_{j=1}^ia_{i,j}$),然后前缀和减一减就完事了。
那么考虑如何维护,首先我们每个区间维护的东西形如这样:

其中不同颜色的交界表示一个修改操作。
容易发现在上一次修改之前(不包含修改的那一刻)的历史总和是固定,后面不会再改变的,但是最后的橙色那段长度是随时间递增的。
那么容易想到对每个区间维护三个值:上一次修改之前的总和 $hsum$,上一次修改的时间 $modi$,当前值(即橙色部分每个切片的值) $sum$,然后查询时下传当前的时间 $T$,区间历史总和就是 $hsum+(T-modi+1)\times sum$。
接下来考虑如何修改。首先考虑合并怎么写,其实很好想,上次修改的时间是两个儿子取较大值,那么 $hsum$ 就要加上另一边在差的这段时间的贡献,可以自己想一想。
接下来是难点,如何下传懒标记(因为你要区间修改嘛)。如果你稍微熟悉一点线段树,就会发现懒标记是一段时间的积累。也就是说,懒标记也要维护一个形如上面那条色彩斑斓的东西的玩意。
另外你也容易发现区间加的懒标记维护的是一段时间的增量,那么我们维护四个值:懒标记的开始时间 $stmark$,懒标记的结束时间 $edmark$,懒标记总增量 $smark$,增量从开始到结束的总和 $mark$。然后下传懒标记时,对区间历史总和的贡献就是 $(smark+sum\times (ed-modi))\times len$,其中 $len$ 是区间长度。
至于懒标记下传给懒标记,仿照这个即可,不多做赘述了。
然后我突然发现其实不需要维护懒标记开始时间,鉴定为研学的时候没纸没笔脑子秀逗导致的,但是代码懒得改了。
复杂度 $O(n\log n)$,常数不小。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(i64 i=(s);i<=(e);i++)
#define fordown(i,s,e) for(i64 i=(s);i>=(e);i--)
using namespace std;
using i64=long long;
#define gc getchar()
inline i64 read(){
i64 x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const i64 N=1e5+5,n=1e5,mod=1e9;
i64 q,mnl[N],mxl[N],mnr[N],mxr[N];
i64 ans[N],a[N],m1,m2;
struct Node{
i64 l,r,pos,v;
};
struct SegTree{
#define mid ((l+r)>>1)
#define ls id<<1
#define rs id<<1|1
#define lson l,mid,ls
#define rson mid+1,r,rs
private:
i64 querysum[N<<2],modi[N<<2],hsum[N<<2];
i64 stmark[N<<2],edmark[N<<2],smark[N<<2],mark[N<<2];
void _PushUp(i64 id){
modi[id]=max(modi[ls],modi[rs]);
querysum[id]=querysum[ls]+querysum[rs];
hsum[id]=hsum[ls]+hsum[rs]+querysum[rs]*(modi[id]-modi[rs])+querysum[ls]*(modi[id]-modi[ls]);
}
void _Modify(i64 id,i64 len,i64 Tm,i64 val){
hsum[id]+=querysum[id]*(Tm-modi[id]);
querysum[id]+=val*len;
modi[id]=Tm;
if(stmark[id]==0){
smark[id]=0;
mark[id]=val;
stmark[id]=edmark[id]=Tm;
}else{
smark[id]+=mark[id]*(Tm-edmark[id]);
mark[id]+=val;
edmark[id]=Tm;
}
}
void _Mark_Modi(i64 id,i64 len,i64 st,i64 ed,i64 sum,i64 val){
hsum[id]+=querysum[id]*(ed-modi[id]);
hsum[id]+=sum*len;
querysum[id]+=val*len;
modi[id]=ed;
if(stmark[id]==0){
smark[id]=sum;
mark[id]=val;
stmark[id]=st;
edmark[id]=ed;
}else{
smark[id]+=mark[id]*(ed-edmark[id]);
smark[id]+=sum;
mark[id]+=val;
edmark[id]=ed;
}
}
void _PushDown(i64 id,i64 len){
_Mark_Modi(ls,((len+1)>>1),stmark[id],edmark[id],smark[id],mark[id]);
_Mark_Modi(rs,len>>1,stmark[id],edmark[id],smark[id],mark[id]);
mark[id]=stmark[id]=edmark[id]=smark[id]=0;
}
public:
void Update(i64 L,i64 R,i64 Tm,i64 X,i64 l=1,i64 r=n,i64 id=1){
if(L<=l&&r<=R){
_Modify(id,r-l+1,Tm,X);
return;
}
if(stmark[id]!=0) _PushDown(id,r-l+1);
if(L<=mid) Update(L,R,Tm,X,lson);
if(mid< R) Update(L,R,Tm,X,rson);
_PushUp(id);
}
i64 Query(i64 L,i64 R,i64 Tm,i64 l=1,i64 r=n,i64 id=1){
if(L<=l&&r<=R){
return hsum[id]+querysum[id]*(Tm-modi[id]+1);
}
if(stmark[id]!=0) _PushDown(id,r-l+1);
i64 res=0;
if(L<=mid) res+=Query(L,R,Tm,lson);
if(mid< R) res+=Query(L,R,Tm,rson);
return res;
}
}mt;
vector<Node> op[N],que[N];
void init(){
m1=m2=1;
forup(i,1,n){
m1=m1*1023%mod;
m2=m2*1025%mod;
a[i]=m1^m2;
}
stack<i64> mns,mxs;
mns.push(0);mxs.push(0);
forup(i,1,n){
while(mns.top()!=0&&a[mns.top()]>=a[i]) mns.pop();
mnl[i]=mns.top()+1;
mns.push(i);
while(mxs.top()!=0&&a[mxs.top()]<=a[i]) mxs.pop();
mxl[i]=mxs.top()+1;
mxs.push(i);
}
while(mns.size()) mns.pop();
while(mxs.size()) mxs.pop();
mns.push(n+1);mxs.push(n+1);
fordown(i,n,1){
while(mns.top()!=n+1&&a[mns.top()]>a[i]) mns.pop();
mnr[i]=mns.top()-1;
mns.push(i);
while(mxs.top()!=n+1&&a[mxs.top()]<a[i]) mxs.pop();
mxr[i]=mxs.top()-1;
mxs.push(i);
}
forup(i,1,n){
op[mnl[i]].push_back(Node{i,mnr[i],0,-a[i]});
op[i+1].push_back(Node{i,mnr[i],0,a[i]});
op[mxl[i]].push_back(Node{i,mxr[i],0,a[i]});
op[i+1].push_back(Node{i,mxr[i],0,-a[i]});
}
}
signed main(){
init();
vector<i64> lsh;
forup(i,1,10){
lsh.push_back(a[i]);
}
sort(lsh.begin(),lsh.end());
lsh.erase(unique(lsh.begin(),lsh.end()),lsh.end());
q=read();
forup(i,1,q){
i64 l1=read(),r1=read(),l2=read(),r2=read();
que[l1-1].push_back(Node{l2,r2,i,-1});
que[r1].push_back(Node{l2,r2,i,1});
}
forup(i,1,n){
for(auto j:op[i]){
i64 l=j.l,r=j.r,v=j.v;
mt.Update(l,r,i,v);
}
for(auto j:que[i]){
i64 l=j.l,r=j.r,v=j.v,pos=j.pos;
ans[pos]+=mt.Query(l,r,i)*v;
}
}
forup(i,1,q){
printf("%lld\n",ans[i]);
}
}
T4
首先,题给你的是个内向基环森林,这点后面会用到。
考虑如何构造,容易发现加的所有边都从点 $1$ 指出必然是不劣的,且基环树的叶子结点必须引一条边。
那么每次找到最深的距离大于 $k$/无法到达(但不能在环上)的点连边,容易发现你连得每条边都是必要的,即这样必定是最优解。
接下来就只有环没处理了,那么问题就转化成了一个环上有若干个黑点与若干个白点,然后你一次操作可以把从指定点 $i$ 开始往后连续的 $k-1$ 个点全部染黑,问把环全染黑的最小操作数。
这个有非常巧妙的贪心。容易发现连续 $k-1$ 个白点(指的不是紧挨着,两个连续的白点可能越过多个黑点),中必定至少有一个要操作一次(不然就涂不完了)。而你涂色操作可以每次跳 $k$ 个 $O(\frac{n}{k})$ 算出一个环至少要操作多少次才完成,那么复杂度就是 $O(k\times \frac{n}{k})=O(n)$!那么我们就能愉快地通过此题了(可能有一些操作实现比较复杂)。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=5e5+5,inf=0x3f3f3f3f;
int n,m,co[N],inc[N],ans;
int to[N],rd[N],dis[N];
int dfn[N],low[N],Tm,ist[N];
stack<int> stk;
vector<vector<int> > cir;
void Tarjan(int x){
low[x]=dfn[x]=++Tm;
ist[x]=1;stk.push(x);
if(!dfn[to[x]]){
Tarjan(to[x]);
low[x]=min(low[x],low[to[x]]);
}else if(ist[to[x]]){
low[x]=min(low[x],dfn[to[x]]);
}
if(dfn[x]==low[x]){
vector<int> vec;
while(stk.top()!=x){
vec.push_back(stk.top());
inc[stk.top()]=1;
ist[stk.top()]=0;
stk.pop();
}
vec.push_back(x);
inc[x]=1;
ist[x]=0;
stk.pop();
if(vec.size()>1){
reverse(vec.begin(),vec.end());
cir.push_back(vec);
}else{
inc[x]=0;
}
}
}
queue<int> q;
signed main(){
n=read();m=read();
forup(i,1,n){
int u=read(),v=read();
to[u]=v;
++rd[v];
}
mem(dis,0x3f);
dis[1]=0;
q.push(1);
forup(i,1,n){
if(!dfn[i]){
Tarjan(i);
}
if(i!=1&&rd[i]==0){
q.push(i);
++ans;
dis[i]=1;
}
}
while(q.size()){
int u=q.front();q.pop();
if(dis[u]>m){
if(inc[u]) continue;
++ans;dis[u]=1;
}
co[u]=1;
rd[to[u]]--;
if(to[u]==1) continue;
if(rd[to[u]]==0) q.push(to[u]);
dis[to[u]]=min(dis[to[u]],dis[u]+1);
}
for(auto vec:cir){
int sz=vec.size();
vector<int> v1,nxt;
int nd=inf;
for(auto i:vec){
nd=min(nd+1,dis[i]);
if(nd<=m) v1.push_back(1);
else v1.push_back(0);
}
forup(i,0,sz-1){
v1.push_back(v1[i]);
}
nxt.resize(sz*2);
int nw=inf,cnt=0,res=inf;
fordown(i,sz*2-1,0){
if(!v1[i]) nw=i;
nxt[i]=nw;
}
int i=nxt[0];
while(i<sz){
int l=i,rr=0;
++cnt;
while(l<i+sz){
++rr;
if(l+m>=i+sz) break;
l=nxt[l+m];
}
i=nxt[i+1];
res=min(res,rr);
}
if(res==inf) res=0;
ans+=res;
}
printf("%d\n",ans);
}