20230824 B 组模拟赛 C 题 题解
前言
这次 C 题挺有意思的。
题解
首先不考虑改造操作,应该如何求贡献。
考虑求出每一条边的贡献,原式子可以这样化:
$$ \begin{aligned} &\sum_{i=1}^{n-1}\sum_{j=i+1}^nf(i,j)a_ia_j\\ =&\sum_{i=1}^{n-1}\sum_{j=i+1}^n\left(\sum_{(u,v)\in P(i,j)}^{v>u}w(u,v)\right)a_ia_j\\ =&\sum_{(u,v)}^{v>u}w(u,v)\sum_{i=1}^n\sum_{j=i+1}^na_ia_j[(u,v)\in P(i,j)]\\ \end{aligned} $$
其中 $P(i,j)$ 表示 $i,j$ 间简单路径上边的集合,中括号为艾佛森括号,表示若内部表达式为真,值为 $1$,反之为 $0$。
容易发现后面那个艾佛森括号里面的表达式成立当且仅当断开边 $(u,v)$ 后,$i,j$ 在两棵不同的树内。
那么 $\sum_{i=1}^n\sum_{j=i+1}^na_ia_j[(u,v)\in P(i,j)]$ 的值其实就是断开 $(u,v)$ 后两棵树的点权和相乘(随便因式分解一下)。
换句话说,每条边的贡献就是由它分开的两部分点权和相乘乘以它的边权。
那么再考虑改造操作,考虑改造操作对总贡献的变化量。
首先考虑有这么一棵树,然后我们要改造的是以绿色节点为根的子树(图示很草,凑合看):
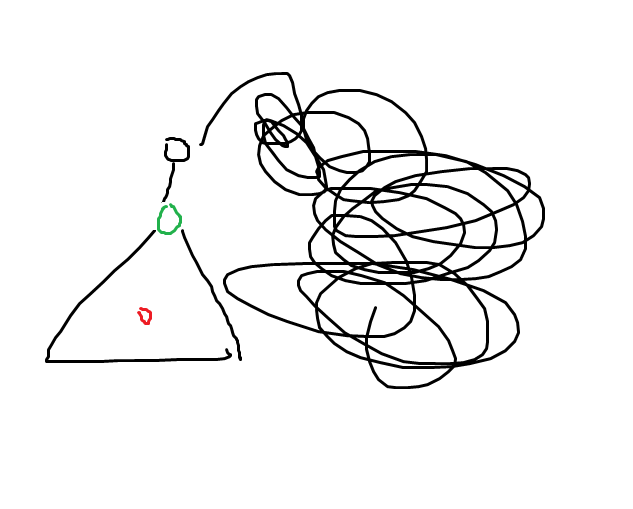
那么假如选择红色节点作为新的根,总贡献会如何变化。
考虑红-绿的路径。
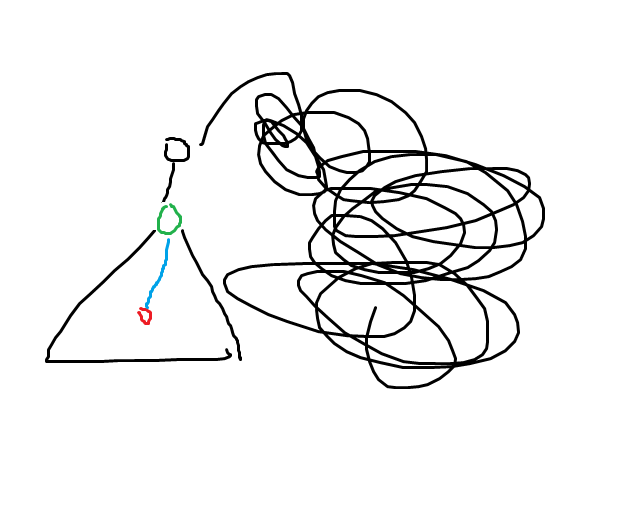
容易发现不在这条路径上的边贡献都不会边,考虑路径上的边贡献会怎么变化。
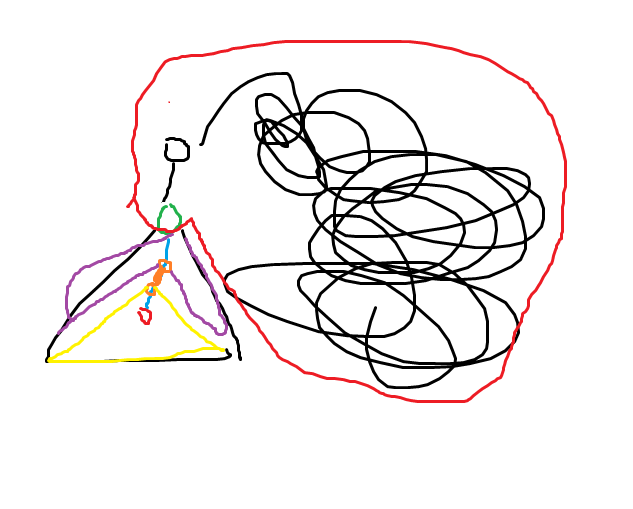
先看这条橙色边,假设它把那棵子树分成黄紫两部分,不妨设橙边边权为 $w$,红色部分和为 $R$,紫色部分和为 $P$,黄色部分和为 $Y$。
那么这条边原先的贡献就是 $w\times(R+P)\times Y$,改造后容易发现原先的黄色部分跑到橙边上面去了,紫色部分跑到橙边下面去了,那么贡献就变成了 $w\times(R+Y)\times P$。
那么差值即为 $w(RP+YP)-w(RY+YP)=w(RP-RY)$。
容易发现假如我们找到了绿点,那么 $Y+P$ 是可以知道的,设这个值为 $S$,显然,$R=sum-S$,其中 $sum$ 为所有点的点权和,但这个我们先放在一边。
那么 $w(RP-RY)=w(R(S-Y)-RY)=R(w(S-Y*2))$
那么考虑 红-绿 整条路径上面的所有边,设 $S_i$ 表示以点 $i$ 为根的子树点权和(或者某条路径所指向的儿子的子树和),绿点为点 $x$,红点为点 $y$,那么改变量总量即为:
$$ \begin{aligned} &(S_1-S_x)\sum_{(u,v)\in P(x,y)}^{v>u}(w(u,v)S_x-2w(u,v)S_{(u,v)})\\ =&(S_1-S_x)S_x\left(\sum_{(u,v)\in P(x,y)}^{v>u}w(u,v)\right)-2\left(\sum_{(u,v)\in P(x,y)}^{v>u}w(u,v)S_{(u,v)}\right) \end{aligned} $$
发现后面两个 $\sum$ 可以直接用前缀和维护那么设 $suma_i=\sum_{(u,v)\in P(1,i)}^{v>u}w(u,v),sumb_i=\sum_{(u,v)\in P(1,i)}^{v>u}w(u,v)S_{(u,v)}$,上面的式子就可以化成:
$$(S_1-S_x)[S_x\left(suma_y-suma_x\right)-2\left(sumb_y-sumb_x\right)]$$
这里的中括号就是普通的方括号。
这个式子很好看,给人一种可以维护的感觉,那么如何维护呢?我们把式子拆开来看。
$$ \begin{aligned} &(S_1-S_x)[S_x\left(suma_y-suma_x\right)-2\left(sumb_y-sumb_x\right)]\\ =&(S_1-S_x)(S_xsuma_y-S_xsuma_x-2sumb_y+2sumb_x)\\ =&(S_1-S_x)(2sumb_x-S_xsuma_x)+(S_1-S_x)(S_xsuma_y-2sumb_y) \end{aligned} $$
这样就好看了,容易发现前面的 $(S_1-S_x)(2sumb_x-S_xsuma_x)$ 是一个只与 $x$ 有关的式子,而后面的 $S_xsuma_y-2sumb_y$ 是一个可以斜率优化的式子,可以在凸包上二分解决,只要按 $S_1-S_x$ 的正负性分类讨论即可。
那么如何对某棵子树上所有点组成的凸包进行二分呢?首先树上问题可以转化为区间问题,那么就转化成对区间的凸包二分。这类似于一个区间取 $\max$,是有结合律的。
简单来说,点集 $A$ 的凸包与点集 $B$ 的凸包得到的答案取最值和点集 $A+B$ 的凸包得到的答案相等。证明显然。
那么有结合律就想到线段树,对线段树每个结点维护上下各一个一个凸包,上传时可以归并地合并(见代码),查询时对区间内每个凸包求出一个答案然后取最值即可,建树复杂度 $O(n\log n)$,查询复杂度 $O(\log^2 n)$,可以通过此题。
本题有个坑点,横坐标相同的多个点只保留最优的那个。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
using i64=__int128;
#define gc getchar()
inline i64 read(){
i64 x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const i64 N=1e5+5,inf=1e35;
int n;
vector<int> e[N];
i64 sum[N],ans,res[N],pref[N],preg[N],a[N],fw[N];
void print(i64 x,bool p=0){
if(x==0){
if(!p) putchar('0');
return;
}
if(x<0){
putchar('-');
x=-x;
}
int a=x%10;print(x/10,1);
putchar(a+'0');
}
int st[N],ed[N],seq[N],Tm;
void dfs(int x){
sum[x]=a[x];
st[x]=++Tm;seq[Tm]=x;
for(auto i:e[x]){
dfs(i);
sum[x]+=sum[i];
}
ed[x]=Tm;
}
void dfs1(int x,int fa){
if(x!=1){
pref[x]=pref[fa]+fw[x];
preg[x]=preg[fa]+fw[x]*sum[x];
}
for(auto i:e[x]){
dfs1(i,x);
}
}
struct SegmentTree{
#define mid ((l+r)>>1)
#define lson l,mid,id<<1
#define rson mid+1,r,id<<1|1
using pii=pair<i64,i64>;
#define fi first
#define se second
#define mkp make_pair
vector<pii> upt[N<<2],dwt[N<<2];
void _Merge(vector<pii> &L,vector<pii> &R,vector<pii> &P,bool up){
int lp=0,rp=0,ls=L.size(),rs=R.size();
while(lp<ls||rp<rs){
pii nw=mkp(0,0);
if(L[lp].fi==R[rp].fi){
if(up){
nw=min(L[lp],R[rp]);
}else{
nw=max(L[lp],R[rp]);
}
++lp;++rp;
}else if(rp>=rs||(lp<ls&&L[lp].fi<=R[rp].fi)){
nw=L[lp];++lp;
}else{
nw=R[rp];++rp;
}
if(up){
while(P.size()>1&&(nw.se-P[P.size()-1].se)*(P[P.size()-1].fi-P[P.size()-2].fi)<=(P[P.size()-1].se-P[P.size()-2].se)*(nw.fi-P[P.size()-1].fi)) P.pop_back();
}else{
while(P.size()>1&&(nw.se-P[P.size()-1].se)*(P[P.size()-1].fi-P[P.size()-2].fi)>=(P[P.size()-1].se-P[P.size()-2].se)*(nw.fi-P[P.size()-1].fi)) P.pop_back();
}
P.push_back(nw);
}
}
void Build(int *A,int l=1,int r=n,int id=1){
if(l==r){
upt[id].push_back(mkp(pref[A[l]],2*preg[A[l]]));
dwt[id].push_back(mkp(pref[A[l]],2*preg[A[l]]));
return;
}
Build(A,lson);Build(A,rson);
_Merge(upt[id<<1],upt[id<<1|1],upt[id],1);
_Merge(dwt[id<<1],dwt[id<<1|1],dwt[id],0);
}
i64 _calc(vector<pii> &V,i64 x,bool up){
if(V.size()==1){
return x*V[0].fi-V[0].se;
}
int ll=1,rr=V.size()-1,mm;
while(ll<rr){
mm=((ll+rr+1)>>1);
if(up){
if((V[mm].fi-V[mm-1].fi)*x>V[mm].se-V[mm-1].se) ll=mm;
else rr=mm-1;
}else{
if((V[mm].fi-V[mm-1].fi)*x<V[mm].se-V[mm-1].se) ll=mm;
else rr=mm-1;
}
}
if(ll==1){
if(up?(V[1].fi-V[0].fi)*x<V[1].se-V[0].se:(V[1].fi-V[0].fi)*x>V[1].se-V[0].se){
ll=0;
}
}
return x*V[ll].fi-V[ll].se;
}
i64 Ask(int L,int R,i64 X,bool up,int l=1,int r=n,int id=1){
if(L<=l&&r<=R){
if(up){
return _calc(upt[id],X,1);
}else{
return _calc(dwt[id],X,0);
}
}
i64 res=0;
if(up){
res=-inf;
if(L<=mid) res=max(res,Ask(L,R,X,up,lson));
if(mid< R) res=max(res,Ask(L,R,X,up,rson));
}else{
res=inf;
if(L<=mid) res=min(res,Ask(L,R,X,up,lson));
if(mid< R) res=min(res,Ask(L,R,X,up,rson));
}
return res;
}
}mt;
signed main(){
freopen("brain.in","r",stdin);
freopen("brain.out","w",stdout);
scanf("%d",&n);
forup(i,1,n){
a[i]=read();
}
forup(i,2,n){
int u=read();fw[i]=read();
e[u].push_back(i);
}
dfs(1);dfs1(1,0);
mt.Build(seq);
forup(i,2,n){
ans+=fw[i]*sum[i]*(sum[1]-sum[i]);
}
forup(i,2,n){
i64 res=(sum[1]-sum[i])*(mt.Ask(st[i],ed[i],sum[i],sum[1]-sum[i]>0)-pref[i]*sum[i]+2*preg[i]);
print(ans+res);
puts("");
}
}