0630 B组模拟赛 题解
前言
还是把另外三道题的题解补上啦。
T1
首先假如我们要判断某个序列能不能构成三角形,很显然只需要排个序然后判相邻三个了。
那么假如我们要构造一个构不成三角形的单调不减序列 $s$ ,那么必定有 $s_{i} \ge s_{i-1}+s_{i-2}$。很显然能最小化 $s_n$ 的情况就是斐波那契数列。打表发现斐波那契数列的第 $45$ 项已经大于 $10^9$ 了。
打表参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
using i64=long long;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=100,inf=0x3f3f3f3f;
i64 a[N];
signed main(){
a[1]=a[2]=1;
int i=2;
while(a[i]<=1e9){
a[i+1]=a[i]+a[i-1];
printf("%lld ",a[i]);
i++;
}
printf("\n%d",i);
}
那么长度大于 $45$ 的区间必定有解,小于 $45$ 的暴力即可,复杂度 $O(45n \log 45)$,常数不是过于夸张就能过。
code
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=1500005,inf=0x3f3f3f3f;
int n,q,a[N],bj[N];
set<int> ss;
signed main(){
// freopen("bitterness.in","r",stdin);
// freopen("bitterness.out","w",stdout);
n=read();q=read();
forup(i,1,n){
a[i]=read();
}
forup(CASE,1,q){
int l=read(),r=read();
if(r-l+1>50){
puts("YES");
continue;
}
vector<int> vec;
forup(i,l,r){
vec.push_back(a[i]);
}
sort(vec.begin(),vec.end());
int len=vec.size()-3;
bool flag=false;
forup(i,0,len){
if(vec[i]+vec[i+1]>vec[i+2]){
puts("YES");
flag=true;
break;
}
}
if(!flag){
puts("NO");
}
}
}
T2
构造题,假如你知道格雷码的话你会发现构造格雷码是满足要求的,但是我不会格雷码 ┓( ´∀` )┏ 所以赛时大寄。
格雷码基本知识
什么是格雷码
格雷码(Gray Code)是一种特殊的 $n$ 位二进制串排列法,它要求相邻的两个二进制串间恰好有一位不同,特别地,第一个串与最后一个串也算作相邻。
格雷码的位数被称为“位”,比如二位格雷码就是 $00,01,11,10$。
如何构造格雷码
假如已经知道了 $x-1$ 位格雷码为 $s_1,s_2\dots,s_n$。
容易得到 $x$ 位格雷码为 $s_1,s_2\dots,s_n,s_n+2^{x-1},s_{n-1}+2^{x-1},\dots,s_2+2^{x-1},s_1+2^{x-1}$。
然后基本上知道上面这些对于这道题就够用了。
首先 $u \to v$ 等价于 $0 \to v \oplus u$,其中 $\oplus$ 表示按位异或,然后为了方便我们可以算 $v \oplus u \to 0$ 然后 reverse 一下。令 $t=v\oplus u$。
首先我们的目标是把 $t$ 中所有 $1$ 变成 $0$,考虑每次固定一个 $1$,不看这个 $1$,把剩下的位数按 $n-1$ 位格雷码遍历一遍(从格雷码上和原来的相等的位置断开然后顺着跑一遍),然后把这一位固定为 $0$,然后因为这一位固定为 $0$ 所以下一次就不能动这一位了,再另外固定一个 $1$,把剩下的位数按 $n-2$ 位格雷码遍历一遍。注意格雷码是一个环状的东西,也就是说遍历一遍后的最后一个和最开始的也只相差一位。所以每次遍历就相当于把一个固定的 $1$ 改成 $0$,然后把某个 $1$ 改成 $0$ 或者 $0$ 改成 $1$。容易发现这对 $1$ 的数量的奇偶性是没有影响的,所以最后必定会剩下一个或者两个 $1$。我们分开解决。
剩下一个
在这种情况下可能还会剩一些位没有固定为 $0$,我们可以每次把某个没有固定的 $0$ 变成 $1$,把原来的 $1$ 固定,最终必定是只有一位没有固定,且它是 $1$,的情况,直接删除即可。
容易发现这样遍历了全部 $2^n$ 个数,故路径长度为 $2^n-1$。
剩下两个
这时候假如我们固定一位遍历格雷码可能会把另一个变成 $0$,这样显然是不好的,注意到格雷码是环形的(反复强调),所以我们只要反方向遍历即可。
然后最后必定会剩下两位没固定为 $0$ 且均为 $1$ 的情况,我们直接构造为 $11\to 10 \to 00$ 即可,注意到这种情况下 $01$ 没有经过,故经过了 $2^n-1$ 个数,路径长度为 $2^n-2$。
code
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=20,inf=0x3f3f3f3f;
int n,s,t,uu,vis[N],cntvv;
vector<int> v[20],ans;
int ppcnt(int x){
int res=0;
while(x){
x^=x&-x;
res++;
}
return res;
}
int calc(int x){// (1)!
int l=n-cntvv,res=0;
fordown(i,n,1){
if(!vis[i]){
res|=((x>>(l-1))&1)<<(i-1);
l--;
}
}
return res;
}
int get(int x){// (2)!
int res=0;
fordown(i,n,1){
if(!vis[i]){
res=(res<<1)|((x>>(i-1))&1);
}
}
return res;
}
void work(int i){// (3)!
vis[i]=1;++cntvv;
int nw=get(t),l=0;
while(v[n-cntvv][l]!=nw) ++l;// (4)!
int len=v[n-cntvv].size();
if((l==0?v[n-cntvv][len-1]:v[n-cntvv][l-1])!=0){// (5)!
forup(j,l,len-1) ans.push_back(calc(v[n-cntvv][j])|(1<<(i-1)));
forup(j,0,l-1) ans.push_back(calc(v[n-cntvv][j])|(1<<(i-1)));
if(l==0) t=calc(v[n-cntvv][len-1]);
else t=calc(v[n-cntvv][l-1]);
}else{
fordown(j,l,0) ans.push_back(calc(v[n-cntvv][j])|(1<<(i-1)));
fordown(j,len-1,l+1) ans.push_back(calc(v[n-cntvv][j])|(1<<(i-1)));
if(l==len-1) t=calc(v[n-cntvv][0]);
else t=calc(v[n-cntvv][l+1]);
}
}
signed main(){
n=read();s=read();t=read();
if(s==t){
puts("0");
printf("%d",s);
return 0;
}
v[0].push_back(0);
forup(i,0,n-1){
vector<int> vv=v[i];
v[i+1]=v[i];
reverse(vv.begin(),vv.end());
for(auto j:vv){
v[i+1].push_back(j|(1<<i));
}
}
uu=s;s^=uu;t^=uu;
while(ppcnt(t)>2){
fordown(i,n,1){
if(t&(1<<(i-1))){
work(i);
break;
}
}
}
if(ppcnt(t)==1){
while(cntvv<n-1){
fordown(i,n,1){
if(t&(1<<(i-1))){
work(i);
break;
}
}
}
ans.push_back(t);
ans.push_back(0);
}else{
while(cntvv<n-2){
fordown(i,n,1){
if(t&(1<<(i-1))){
work(i);
break;
}
}
}
ans.push_back(t);
t^=t&-t;
ans.push_back(t);
t^=t&-t;
ans.push_back(t);
}
reverse(ans.begin(),ans.end());
printf("%d\n",(int)ans.size()-1);
for(auto i:ans){
printf("%d ",i^uu);// (6)!
}
}
- 知道格雷码填进原数
- 知道原数求格雷码
- 固定 $i$,遍历剩下没固定的
- 先固定第 $i$ 为 $0$,后面加上即可
- 保证绕一圈不变为 $0$
- 输出时记得异或回去
T4
注意
本文中称题目给的每个区间为“实际区间”,询问的区间为“询问区间”。
首先经典地我们可以把询问离线下来,按询问区间右端点排序,把询问挂在右端点,每次加入最新的实际区间然后询问左端点。
注意到区间覆盖不好维护,考虑维护端点。具体来说,维护询问区间内所有实际区间放在一起会产生多少个点一侧有区间另一侧没有区间,这个数量除以二就是区间数量。
我们把实际区间的覆盖看做一个涂色的过程,我们只考虑每个点最后一次被覆盖,这是显然的,因为每个点无论前面被覆盖了几次它能否成为端点也只和最后一次覆盖有关。现在假如给我们的区间序列长这样:
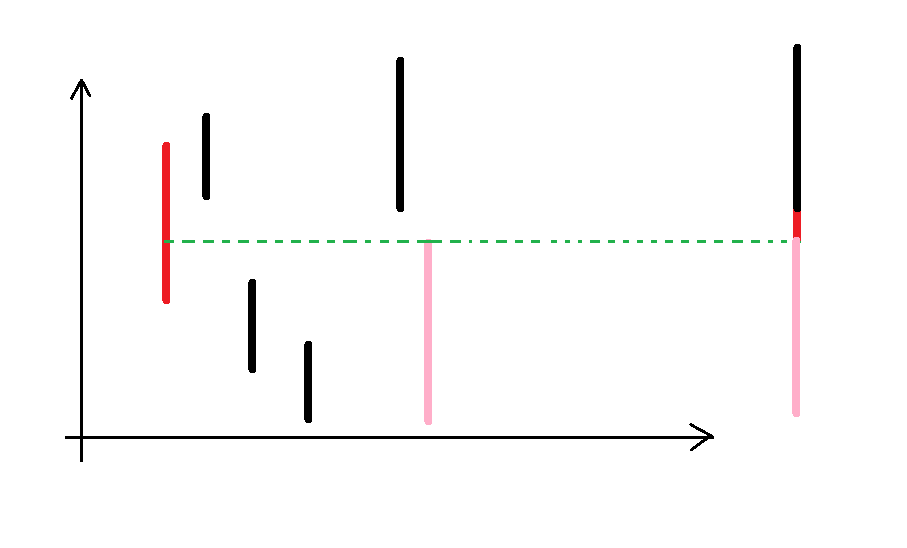
那么它最后覆盖出来就是右边的那样,我们考虑绿色的这根虚线在实际区间上对应的点什么时候会产生贡献。
显然,在时间区间右端点在粉色右边,左端点在红色和粉色中间(左开右闭)时,这个点就是一个端点由于我们是把询问挂在右端点上的,第一个条件肯定满足,那么我们只需要维护第二个条件即可。以下为了方便叙述,称像这样左右颜色不同的点为关键点。
那么加一个区间就会使它中间的所有关键点贡献归零,然后产生两个新的关键点。我们可以用 map 维护关键点和每个关键点左右的颜色,然后用树状数组维护区间的加减,每次加右区间查左区间即可。
code
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
using pii=pair<int,int>;
#define fi first
#define se second
#define mkp make_pair
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=4e5+5,M=1e6+5,inf=0x3f3f3f3f;
int n,q,l[N],r[N];
struct Node{
int L,R,pos;
}que[M];
bool cmp(Node a,Node b){
return a.R<b.R;
}
int ans[M];
struct Tree{
int c[N];
void upd(int x,int k){++x;for(;x<=n+1;x+=x&-x)c[x]+=k;}
int sum(int x){++x;int res=0;for(;x>0;x-=x&-x)res+=c[x];return res;}
}mt;
map<int,pii> mp;
void insert(int l,int r,int x){
map<int,pii>::iterator it=mp.lower_bound(l),jt=mp.upper_bound(r);
int il=prev(it)->se.se,jr=jt->se.fi;
for(map<int,pii>::iterator kt=it;kt!=jt;){
int be=min(kt->se.fi,kt->se.se),ed=max(kt->se.fi,kt->se.se);
mt.upd(be+1,-1);mt.upd(ed+1,1);
++kt;
mp.erase(prev(kt));
}
mp[l]=mkp(il,x);mp[r]=mkp(x,jr);
mt.upd(il+1,1);
mt.upd(x+1,-1);
mt.upd(jr+1,1);
mt.upd(x+1,-1);
}
signed main(){
n=read();q=read();
forup(i,1,n){
l[i]=read();
r[i]=read();
}
forup(i,1,q){
que[i].L=read();
que[i].R=read();
que[i].pos=i;
}
sort(que+1,que+q+1,cmp);
mp[0]=mp[1e9+1]=mkp(0,0);
int rr=1;
forup(i,1,q){
while(rr<=n&&rr<=que[i].R){
insert(l[rr],r[rr],rr);
++rr;
}
ans[que[i].pos]=mt.sum(que[i].L);
}
forup(i,1,q){
printf("%d\n",ans[i]/2);
}
}