0426 C组模拟赛 题解
T1 题解
部分分暴力 $DFS$,后面两个特殊点可以用最大的一半和最小的一半匹配,不展开讲。
首先题意等价为选 $\dfrac{n}{2}$ 个 $i$ 的 $r$ 加起来,减去其他数的 $l$,求最大值。考虑贪心。
首先全选 $r$,把第 $i$ 个换成选 $l$ 就会使总和减小 $-l_i-r_i$,换句话说,把第 $i$ 个选成 $l$ 的代价是 $l_i+r_i$。
贪心选最小的 $\dfrac{n}{2}$ 个代价即可。
code
code
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(register int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(register int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=1e6+5,inf=0x3f3f3f3f;
int n,l[N],r[N];
long long lrlr[N],ans;
signed main(){
n=read();
forup(i,1,n){
l[i]=read();r[i]=read();
ans+=r[i];
lrlr[i]=l[i]+r[i];
}
sort(lrlr+1,lrlr+n+1);
forup(i,1,n/2){
ans-=lrlr[i];
}
printf("%lld",ans);
}
T2 题解
这道题我没钻研过就不讲部分分了。
树上背包合并。
考虑枚举种族 $i$ 可能会造反,一个连通块中每有一个种族 $i$ 就产生 $1$ 贡献,反之产生 $-1$ 贡献,转化为求贡献大于 $0$ 的连通块个数。
考虑 $dp_{i,j}$ 表示 $i$ 的子树中包括 $i$ 的连通块有多少个值为 $j$(注意处理负数下标),依次将当前节点与每个子节点合并。
关于如何合并,枚举当前连通块 $u$ 的值 $j$ 与子节点 $v$ 的值 $k$,使得 $dp_{u,j+k}$ 增加 $dp_{u,j}\cdot dp_{v,k}$,需要注意开一个临时数组存不然可能出现错误。
每次枚举只需要枚举有意义的部分,其他负无穷的值略过,即对于每个节点存一个上界和下界来转移,并且只需要保留 $-cnt$ 至 $cnt$ 的部分($cnt$ 为整棵树中当前颜色的数量),就能卡过去了。
关于复杂度,树上背包复杂度是 $O(nk)$ 的,这里 $k$ 即为 $cnt$,而 $\sum cnt=n$,故复杂度为 $O(n^2)$,由于转移时是 $O(n)$ 带小常数,所以总的复杂度是 $O(n^3)$ 带小常数。
code
code
#include<bits/stdc++.h>
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(register ll i=(s);i<=(e);i++)
#define fordown(i,s,e) for(register ll i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline ll read(){
ll x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const ll N=3005,inf=0x3f3f3f3f,add=3005,mod=998244353;
ll n,c[N],cnt[N],ans;
vector<ll> e[N];
ll dp[N][N<<1],sv[N<<1],mn[N],mx[N];
ll nwco;
void dfs(ll x,ll fa){
forup(i,-cnt[nwco],cnt[nwco]){
dp[x][i+add]=0;
}
if(c[x]==nwco){
dp[x][1+add]=1;
mx[x]=mn[x]=1;//存储上下界
}else{
dp[x][-1+add]=1;
mx[x]=mn[x]=-1;
}
for(auto i:e[x]){
if(i==fa) continue;
dfs(i,x);
forup(j,mn[x],mx[x]){
sv[j+add]=dp[x][j+add];
}
forup(j,mn[x],mx[x]){
forup(k,mn[i],mx[i]){
if(dp[x][j+add]==0||dp[i][k+add]==0||j+k>cnt[nwco]||j+k<-cnt[nwco]) continue;
sv[j+k+add]=(sv[j+k+add]+dp[x][j+add]*dp[i][k+add]%mod)%mod;
mn[x]=min(mn[x],j+k);
mx[x]=max(mx[x],j+k);
}
}
forup(j,mn[x],mx[x]){
dp[x][j+add]=sv[j+add];sv[j+add]=0;
}
}
forup(i,1,mx[x]){
ans=(ans+dp[x][i+add])%mod;
}
}
signed main(){
n=read();
forup(i,1,n){
c[i]=read();
cnt[c[i]]++;
}
forup(i,1,n-1){
ll u=read(),v=read();
e[u].push_back(v);e[v].push_back(u);
}
forup(i,1,n){
if(!cnt[i]) continue;
nwco=i;
dfs(1,0);
}
printf("%lld",ans);
}
T3 题解
子任务 #1 20pts
设 $dp_i$ 表示从 $i$ 到 $n$ 的最大心情值,有一个显然的 dp 式子。
$$dp_i=\max\limits_{j=i+1}^{i+T_i}{dp_j+H_i-\left\lfloor \frac{j-i}{K} \right\rfloor\cdot D}$$
边界条件是 $dp_n=H_n$,特判即可,可以 $O(n)$ 转移,复杂度 $O(n^2)$。
子任务 #3 子任务 #4
子任务 #3 中,$K=1$,此时下取整不会影响,#4 中,$K=n$,此时疲劳度始终为 $0$,这两个点可以直接用线段树维护,复杂度 $O(n\log n)$。
90pts
其实棺方题解说这个方法可以 AC,但是我不太信 $O(n\log^2n)$ 可以过 $10^6$。
我们发现下取整非常麻烦,因为难以把 $i$ 和 $j$ 分别拆出来,但思考一下发现其实可以拆出来。
先不看后面的系数 $D$,那个式子可以这样转化:
令 $I=i \bmod K,J=j\bmod K$
$$\left\lfloor \frac{j-i}{K} \right\rfloor=\left\lfloor \frac{\left\lfloor\frac{j}{K}\right\rfloor\cdot K+J -(\left\lfloor\frac{j}{K}\right\rfloor\cdot K +I)}{K}\right\rfloor=\left\lfloor\left\lfloor\frac{j}{K}\right\rfloor-\left\lfloor\frac{i}{K}\right\rfloor+\frac{J-I}{K}\right\rfloor$$
由于前面两项都是整数所以可以直接提出来,则上式可化为:
$$\left\lfloor\frac{j}{K}\right\rfloor-\left\lfloor\frac{i}{K}\right\rfloor+\left\lfloor\frac{J-I}{K}\right\rfloor$$
由于 $J < K,I<K$,所以 $\left\lfloor\frac{J-I}{K}\right\rfloor$ 必定等于 $0$ 或 $-1$,当且仅当 $J <I,\left\lfloor\frac{J-I}{K}\right\rfloor=-1$。
故 20pts 的 dp 式子可化为:
$$dp_i=\max\limits_{j=i+1}^{i+T_i}{dp_j+H_i-\left\lfloor\frac{j}{K}\right\rfloor\cdot D+\left\lfloor\frac{i}{K}\right\rfloor\cdot D+[j \bmod K < i\bmod K]\cdot D}$$
其中中括号表示满足该条件时该表达式的值为 $1$(注意 $-1$ 与前面的减号负负得正就变成加号了)。
然后我们把带 $i$ 的式子拆出来:
$$dp_i=\max\limits_{j=i+1}^{i+T_i}{dp_j-\left\lfloor\frac{j}{K}\right\rfloor\cdot D+[j \bmod K < i\bmod K]\cdot D}+H_i+\left\lfloor\frac{i}{K}\right\rfloor\cdot D$$
令 $f_j=dp_j-\left\lfloor\frac{j}{K}\right\rfloor\cdot D$:
$$dp_i=\max\limits_{j=i+1}^{i+T_i}{f_j+[j \bmod K < i\bmod K]\cdot D}+H_i+\left\lfloor\frac{i}{K}\right\rfloor\cdot D$$
接下来我们只需要考虑那个让人头疼的中括号了。
注意到,假如我们把所有 $\left\lfloor\frac{j}{K}\right\rfloor$ 相等的 $j$ 分为一块,满足那个式子的一定在一个连续的区间内,且一定是这一块的前缀。
画个图理解一下,我们把所有 $\left\lfloor\frac{j}{K}\right\rfloor$ 相等的 $j$ 放在同一列,模数相同的放在同一行。
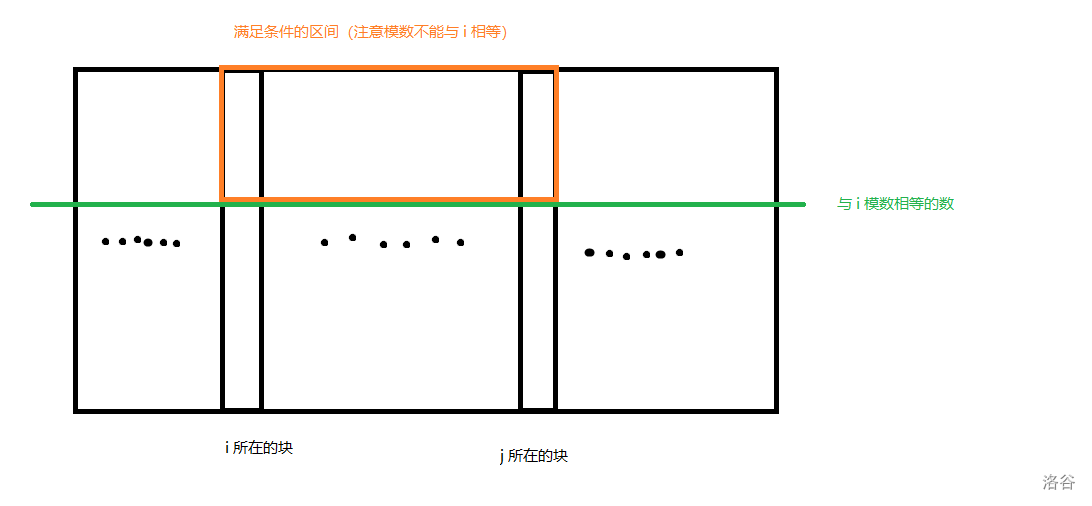
这启发我们用一个二维树状数组维护(或者笼统地说,树状数组套树状数组)。
对于每个模数(即上图中每一行),维护一个求前缀最大值树状数组,然后把这些树状数组压到一棵纵向的树状数组里,用来求二维区间最大值。
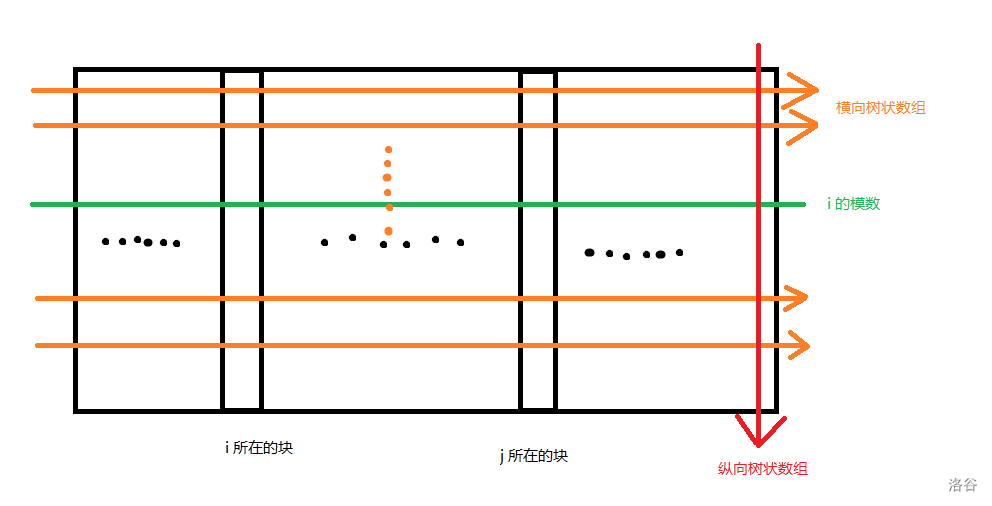
这样我们就能在 $O(\log^2n)$ 的时间内查询某个矩形内的最大值。
接下来我们考虑要查询哪些区间,带哪个式子。
分两种情况讨论:
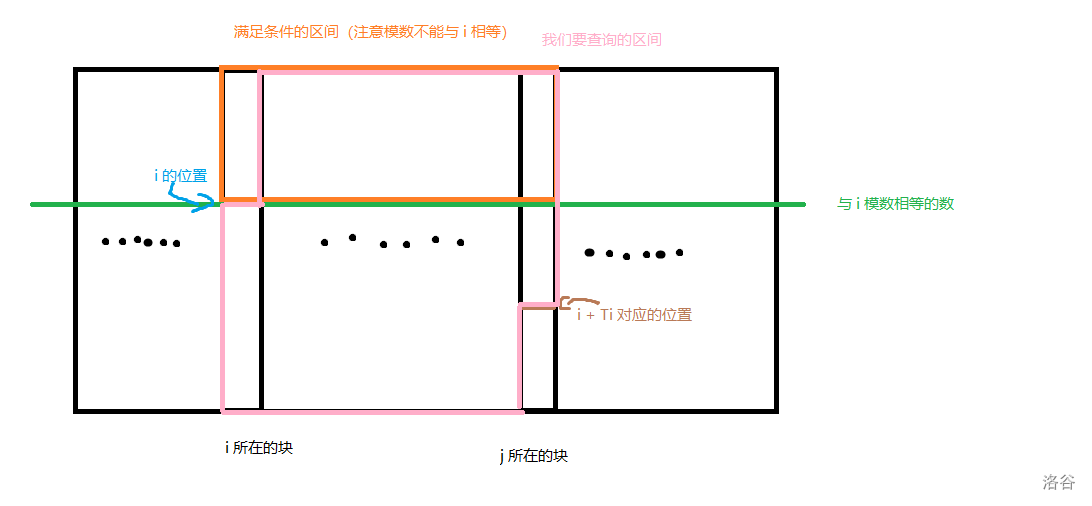
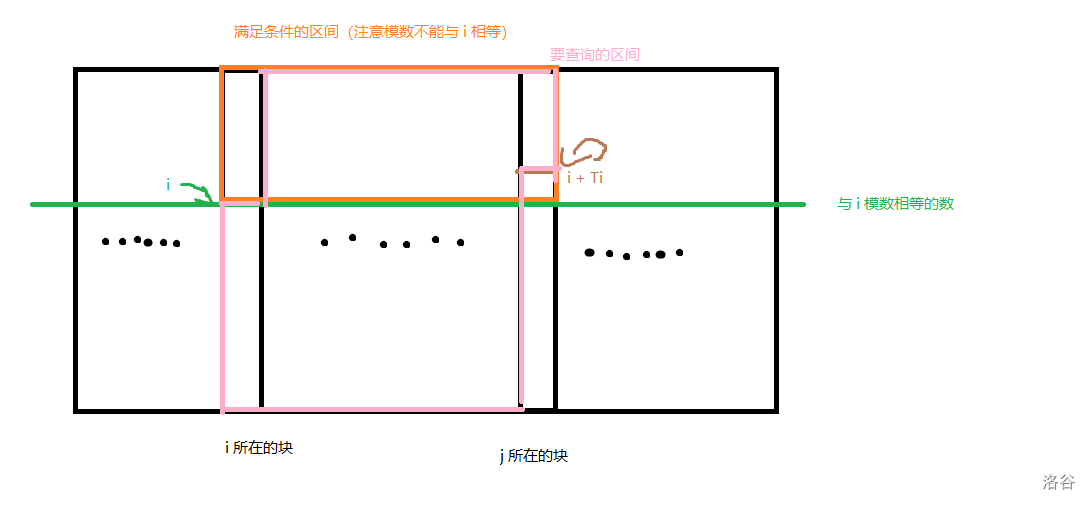
这种情况下,$i+T_i$ 的模数大于 $i$ 的模数,我们需要查询以下几个区间。
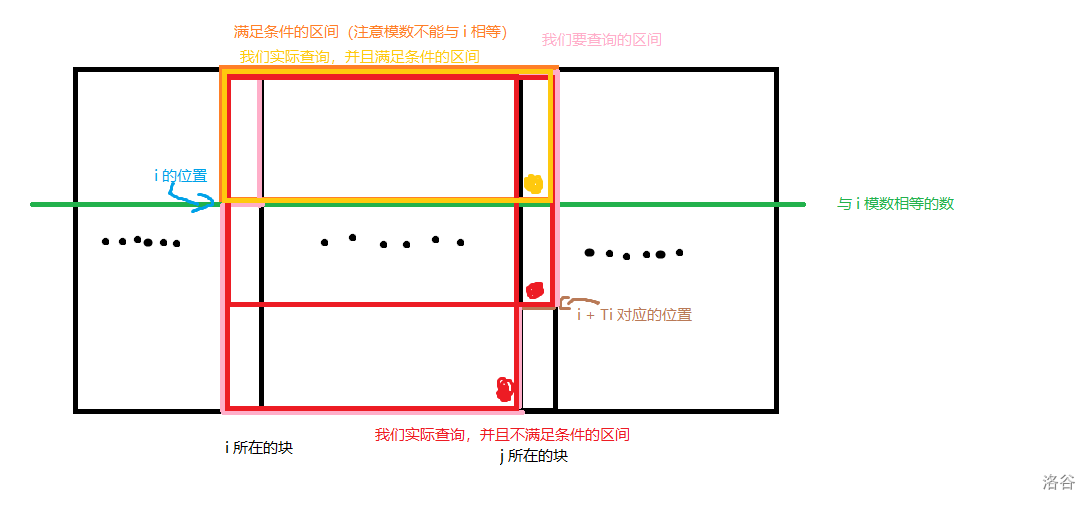
上图几个彩色圆点即我们查询的点,前面多查的部分都赋为 $-\infty$ 所以不用管。
有人可能有问题:为什么红色部分和黄色部分带两个不同的式子,但红色部分包含了黄色部分。
欸这你就问对人了,我昨晚做梦都在想这个问题。
思考一个问题,黄色部分带的式子等于红色部分加 $1$,也就是说假如红色部分的最大值在黄色部分里,那么它并不会对答案产生贡献,可以忽略。
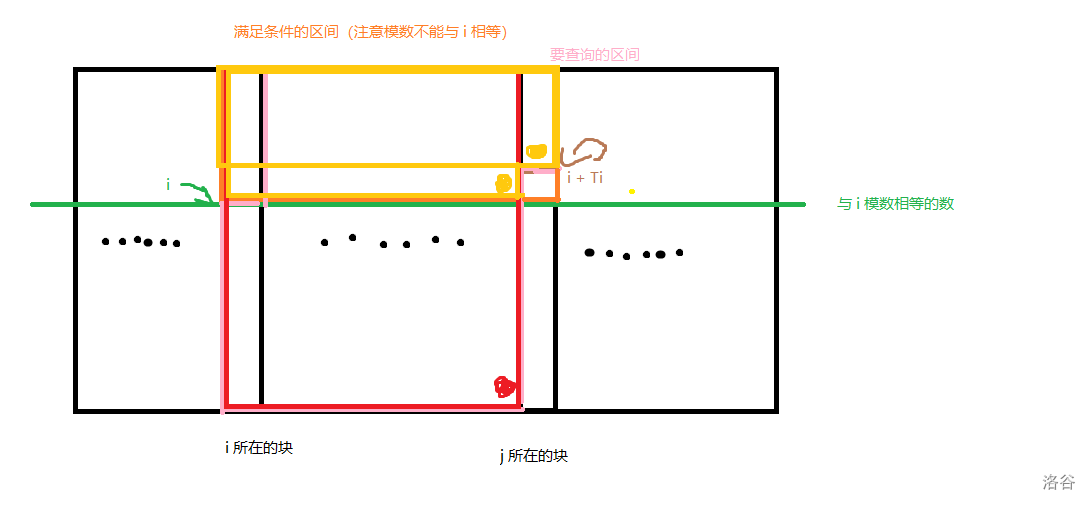
另一种情况:
同理,不解释了。
复杂度 $O(n \log \frac{n}{K}\cdot\log K)$ 题解说能过 $2 \times 10^6$,但我不信。
100 pts
注意到每一列只有求前缀操作,且处理完当前列后就不会修改,想到纵向维度上并不需要树状数组,我们对当前列单独开一个树状数组,每次清空,处理完当列后顺着跑一边前缀最大值上传到对应的横向树状数组中。
复杂度 $O(n \log \frac{n}{K})$。
需要注意,100pts 做法和 90pts 做法都需要用 vector 动态开空间来防止 MLE。
code
code
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(register ll i=(s);i<=(e);i++)
#define fordown(i,s,e) for(register ll i=(s);i>=(e);i--)
using namespace std;
typedef long long ll;
#define T (1<<15)
char buf[T],*p1=buf,*p2=buf;
#define nc() (p1==p2&&(p2=buf+fread(p1=buf,1,T,stdin),p1==p2)?-1:*p1++)
ll read(){//题目给的快读,赞美好题!
ll x=0;char c;bool s=0;
do c=nc();while(c!=45&&(c<48||c>57));
if(c==45)c=nc(),s=1;
do x=10*x+(c&15),c=nc();while(c>=48&&c<=57);
return s?-x:x;
}
#undef T
const ll N=2e6+5,inf=1e18;
ll n,K,D,h[N],t[N],dp[N],blg[N],L[N],R[N];
void mymax(ll& a,ll b){
if(a<b) a=b;
}
struct Tree1{
vector<ll> c;
ll sz;
void resz(ll x){c.resize(x+1);sz=x;forup(i,1,sz)c[i]=-inf;}
void Upd(ll x,ll k){
for(;x<=sz;x+=x&-x){
if(c[x]>k)break;
c[x]=k;
}
}
ll Ask(ll x){ll res=-inf;for(;x>0;x-=x&-x)res=max(res,c[x]);return res;}
}nt;
vector<Tree1> mt;
signed main(){
n=read();K=read();D=read();
mt.resize(K+1);
forup(i,0,K){
mt[i].resz((n+K-1)/K+1);
}
forup(i,1,n){
h[i]=read();
}
forup(i,1,n-1){
t[i]=read();
}
ll cnt;//块数
for(int i=1;R[i-1]!=n;++i){
cnt=i;
L[i]=max((i-1)*K,1ll);R[i]=min(i*K-1,n);
forup(j,L[i],R[i]){blg[j]=i;}
}
fordown(bl,cnt,1){
nt.resz(K+1);//清空当前树状数组
fordown(i,R[bl],L[bl]){
ll pipi=i%K;//在哪一行
if(i==n){//n 要特判
dp[i]=h[i];
nt.Upd(pipi+1,dp[i]-i/K*D);
continue;
}
ll rted=min(t[i]+pipi+1,K);//在当前块最右能取到哪里
ll res=-inf;
mymax(res,nt.Ask(rted)+i/K*D);
if(t[i]+pipi+1<=K){//如果 i+T 就在当前行可以直接跳过
dp[i]=res+h[i];
nt.Upd(pipi+1,dp[i]-i/K*D);
continue;
}
ll post=blg[i+t[i]],ppt=(pipi+t[i])%K;//Ti+i 的行数和列数
if(ppt>=pipi-1){
if(pipi!=0) mymax(res,mt[pipi-1].Ask(post)+i/K*D+D);
//注意不取等,所以要减一
mymax(res,mt[K-1].Ask(post-1)+i/K*D);
mymax(res,mt[ppt].Ask(post)+i/K*D);
}else{
mymax(res,mt[pipi-1].Ask(post-1)+i/K*D+D);
mymax(res,mt[K-1].Ask(post-1)+i/K*D);
mymax(res,mt[ppt].Ask(post)+i/K*D+D);
}
dp[i]=res+h[i];//统计答案
nt.Upd(pipi+1,dp[i]-i/K*D);//上传到当前树状数组
}
ll mx=-inf;//前缀最大值
forup(i,L[bl],max(R[bl],L[bl]+K-1)){
//处理完后順向上传前缀最大值
if(i<=R[bl]) mymax(mx,dp[i]-i/K*D);
mt[i%K].Upd(bl,mx);
}
}
ll ans=0;
forup(i,1,n){
// printf("%lld ",dp[i]);
ans^=(dp[i]+i);
}
printf("%lld",ans);
}