进化（D.cpp 1S 512M）

传送门

题解

首先，\(b[i]=(a[i+1]+a[i-1])\bmod 2\) 等价于 \(b[i]=a[i+1] \oplus a[i-1]\)。

我们考虑一种暴力做法。

假设进化 \(m\) 次后的数组为 \(a_m\)，那么注意到 \(a_m[i]\) 可以转移到 \(a_{m+1}[i+1]\) 和 \(a_{m+1}[i-1]\)。

抽象一下，会发现对于每个 \(i\)，\(a_1[i]\) 有 \(2^T\) 种路径转移到 \(a_T\)。

我们可以把每一条路径用一个二进制数（bitset？）概括一下（\(0\) 表示向左，\(1\) 表示向右），枚举路径判断每个 \(a_1[i]\) 对 \(a_T\) 的影响。

复杂度 \(O(n 2^T)\)，~~连最小的部分分都过不了。~~

但是这个做法有巨大的优化空间，首先容易发现，并不需要枚举每条路径，因为每条路径的终点与且仅与路径中 \(0\)/\(1\) 的个数有关，我们利用组合数可以把复杂度压至 \(O(n^2)\)（假如有某种方法可以预处理极其巨大的组合数）。

但这还远不是这条思路的极限，假设每个 \(i\) 到 \(j\) 的路径中有 \(r\) 个 \(1\)，显然有 \(T-r\) 个 \(0\)。

那么可以得到 \(j-i=r-(T-r)=2r-T\)。

注意到，\(i\) 对 \(j\) 的影响只与 \(a_1[i]\) 和 \(\dbinom{T}{r}\) 的奇偶性有关，概括成数学语言 \(i\) 对 \(j\) 的影响就是 \(\dbinom{T}{r}\bmod 2 \cdot a_1[i]\)（这个 \(r\) 是可以求出来的但我们暂且放一放）。

看到组合数模一个小质数的形式想到 lucas 定理，即：

\[\dbinom{T}{r}\bmod 2=\dbinom{\left\lfloor T/2 \right\rfloor}{\left\lfloor r/2 \right\rfloor}\cdot \dbinom{T \bmod 2}{r\bmod 2}\bmod 2\]

左边还可以再拆但是我不想写了，我们换一种写法，将 \(T\) 在二进制下的第 \(c\) 位记作 \(T_{c}\)（其实并不存在这样的记法只是我为了方便叙述乱搞的），\(r\) 同理。

\[\dbinom{T}{r}\bmod 2 = \dbinom{T_{1}}{r_{1}}\cdot\dbinom{T_{2}}{r_{2}}\cdots \dbinom{T_{\log_T}}{r_{\log T}}\]

注意到 \(\dbinom{T_{c}}{r_{c}}\) 其实只有 \(\dbinom{0}{0}=1,\dbinom{1}{1}=1,\dbinom{0}{1}=0,\dbinom{1}{0}=1\) 四种可能。发现当 \((T)_c=0\) 时结果与且仅与 \((r)_c\) 有关，想到将原先 \(T\) 的每一位拆出来分别计算，下次计算时就由这次的结果为基础，以构造成 \(10\dots00\) 的形式（通过部分分也可以想到这一点），设每次拆出来的数为 \(t\)。

所以 \(\dbinom{t}{r}\bmod 2 = 1\) 当且仅当 \(\forall (t)_c=0,(r)_c=0\)。

换句话说，只有当 \(r\) 的二进制为 \(10\dots00\) 或者 \(00\dots00\) 时，\(\dbinom{t}{r}\bmod 2=1\)。

进一步，\(\dbinom{t}{r}\bmod 2=1\) 当且仅当 \(r=0\) 或 \(r=t\)。

由于 \(j-i=2r-t\)，故 \(a_t[j]\) 只会被 \(a_1[j-t]\) 和 \(a_1[j+t]\) 影响。概括成数学语言就是 \(a_t[j]=a_1[j-t]\oplus a_1[j+t]\)。

但是这里有个问题，数组会越界。

容易想到把它转化成一个等价的环形问题（~~其实并不容易~~）。

考虑构造一个环 \(c\)，它长这样：

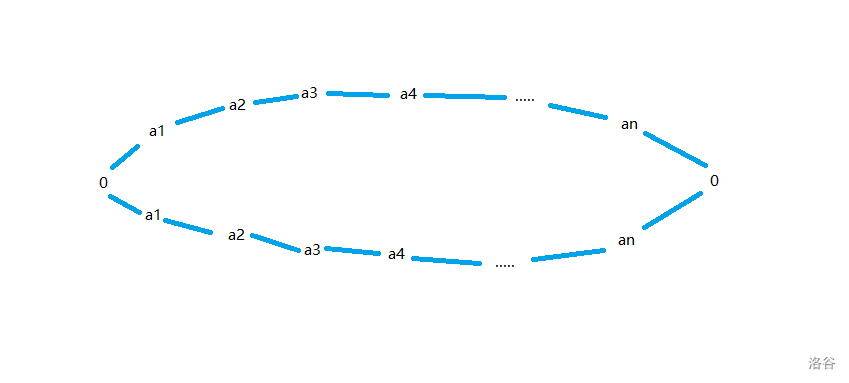
在环 \(c\) 中进行题目描述中的“进化”操作和 \(a\) 是等价的。

首先，每个 \(a[2]\) 到 \(a[n-1]\) 中显然是等价的。

\(a[1]\) 和 \(a[n]\) 的另一边为 \(0\) 显然也是等价的。

对于两端的 \(0\)，它的两侧永远都是相等的，无论何时都是 \(0\)。

（~~我也不知道是怎么想出来的，反正也不是我想出来的。~~）

用数组存的时候左边那个 \(0\) 下标设为 \(0\) 然后顺时针转就行了。

综上，最终做法如下：

取出 \(T\) 二进制最低位（记为 \(t\)），将 \(T\) 减去 \(t\)。
通过现有数组 \(a\) 构造出环 \(c\)。
对于所有 \(1\le i \le n\)，计算出 \(b[i]=c[(i+t)\bmod (n\times 2+2) ] \oplus c[(i-t)\bmod (n\times 2+2) ] \)（注意取模考虑负数）。
将整个 \(b\) 赋给 \(a\)。
重复以上操作直至 \(T\) 归零。

最终的数组 \(a\) 即为答案。

每一层复杂度 \(O(n)\)，最多有 \(\log T\) 层，时间复杂度 \(O(n\log T)\)，空间复杂度 \(O(n)\)，可以通过此题。

code

#include<iostream>
#include<algorithm>
#include<string.h>
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
#include<vector>
#define pbk(a) emplace_back(a)
#define forup(i,s,e) for(register ll i=(s);i<=(e);i++)
#define fordown(i,s,e) for(register ll i=(s);i>=(e);i--)
#define abs(x) (((x)^((x)>>63))-((x)>>63))
using namespace std;
#define gc getchar()
inline ll read(){
    ll x=0,f=1;char c;
    while(!isdigit(c=gc)) if(c=='-') f=-1;
    while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
    return x*f;
}
#undef gc
const ll N=2e5+5,inf=0x3f3f3f3f;
ll t,n;
char b[N];
bool a[N],c[N*2];
ll mymod(ll a,ll b){
    if(a<0) a+=((-a+b-1)/b)*b;
    return a%b;
}
signed main(){
    t=read();n=read();
    scanf(" %s",b+1);
    forup(i,1,n){
        a[i]=b[i]-'0';
    }
    while(t){
        ll kk=t&-t;
        t-=kk;
        forup(i,1,n){
            c[i]=c[n*2+2-i]=a[i];
        }
        forup(i,1,n){
            a[i]=c[mymod(i+kk,n*2+2)]^c[mymod(i-kk,n*2+2)];
        }
    }
    forup(i,1,n){
        printf("%d",a[i]);
    }
}

进化（D.cpp 1S 512M）

题解

code

评论