Skip to content

染色 题解

传送门

题解

感谢hfy提供的大体思路

观察到数据范围是 $10^5$ ,也就是说需要至多 $O(n \log n+q \log n)$ 的算法，我们考虑二分。

题目给的染色条件有点难判断，(为方便叙述,我们定义一条边所在直线多边形一侧为“里”，另一侧为“外”），容易发现，当且仅当一个点在至多 $\dfrac{n}{2}-1$ 条边外时，此点被染色。

即若一个点 $i$ 在 $k_i$ 边外， $\forall k_i \le \dfrac{n}{2}-1,i$被染色

容易发现，若定义任意一对对边为基准边，则对于点 $i$ 同时在两边内，必被染色；同时在两边外，必不被染色；若位于一边以内另一边以外，才需要运用以上性质。

由于我们需要二分（伏笔回收），我们考虑寻找单调性。发现若将平面按基准边的中线（其实不必要是中线），两侧的 $k_{i_1}$ 和 $k_{i_2}$ 分别关于边的编号单调。（淦我在写什么但反正都是我自己看）（但是想想不放个图解估计明天就看不懂了，而且万一有别人要看呢）

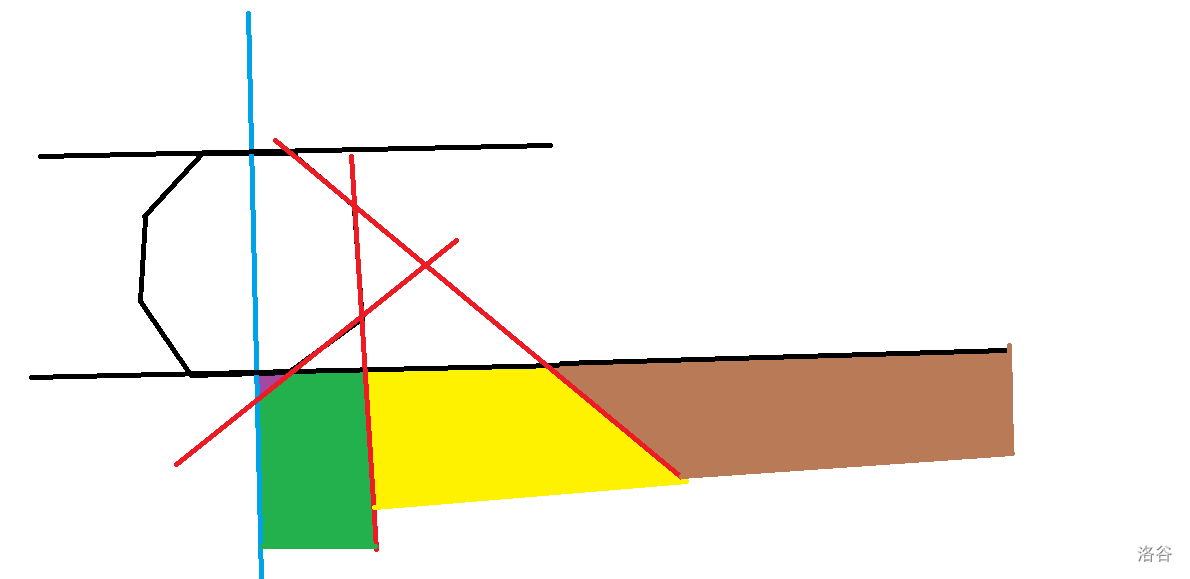
（仅考虑右半部分）一个点在上图中棕色部分时，在且仅在上基准边内。在黄色部分会多一条边，绿色部分会再多一条边，紫色部分（好小）又会多一条边。这就具有了二分的资本。

综上，我们梳理下做法。

  1. 读入时确定一组基准边，并将每一条边用一次函数按远离其中一条基准边的顺序存入。
  2. 对于每个询问，先确定是否同时在两条基准边内/外，若是，直接输出答案。
  3. 若不是，分别对两侧的边进行二分，算出 $k_i$ ,得出答案。

Code

code 
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,x[N],y[N];
int q,a,b;
double sx,sy;
struct Node{
    bool s,fl;//s true->竖向边; fl true->左侧/下方
    double k,b;// s true->b代表横坐标
};
Node lt[N],rt[N],upl,dwl;
int k1,k2=1;
Node ist(int a1,int b1){
    Node l;
    if(x[a1]==x[b1]){
        l.s=true;
        l.b=y[a1];
        if(sx<x[a1]){
            l.fl=true;
        }else{
            l.fl=false;
        }
    }else{
        l.s=false;
        l.k=double(y[b1]-y[a1])/(x[b1]-x[a1]);//一次函数
        l.b=y[a1]-x[a1]*l.k;
        if(sy<=sx*l.k+l.b){
            l.fl=true;
        }else{
            l.fl=false;
        }
    }
    return l;
}
bool pd(Node l,int a1,int b1){
    if(l.fl){
        if(l.s){
            return a1<=l.b;
        }else{
            return b1<=a1*l.k+l.b;
        }       
    }else{
        if(l.s){
            return a1>=l.b;
        }else{
            return b1>=a1*l.k+l.b;
        }       
    }
}
bool chk(int x1,int y1){
    if(pd(upl,x1,y1)&&pd(dwl,x1,y1)) return true;
    if(!pd(upl,x1,y1)&&!pd(dwl,x1,y1)) return false;
    int ll=1,rr=(n>>1)-1,mm,res=1;
    if(pd(upl,x1,y1)){ //二分
        while(ll<=rr){
            mm=(ll+rr)>>1;
            if(pd(lt[mm],x1,y1)) ll=mm+1;
            else rr=mm-1;
        }
        res+=rr;
        ll=1;rr=(n>>1)-1;
        while(ll<=rr){
            mm=(ll+rr)>>1;
            if(pd(rt[mm],x1,y1)) ll=mm+1;
            else rr=mm-1;
        }
        res+=rr;
        if(res>(n>>1)) return true;
        return false;       
    }else{
        while(ll<=rr){
            mm=(ll+rr)>>1;
            if(!pd(lt[mm],x1,y1)) ll=mm+1;
            else rr=mm-1;
        }
        res+=(n>>1)-ll;
        ll=1;rr=(n>>1)-1;
        while(ll<=rr){
            mm=(ll+rr)>>1;
            if(!pd(rt[mm],x1,y1)) ll=mm+1;
            else rr=mm-1;
        }
        res+=(n>>1)-ll;
        if(res>(n>>1)) return true;
        return false;   
    }
}
signed main(){
    scanf("%lld",&n);
    for(int i=1;i<=n;i++){
        scanf("%lld%lld",&x[i],&y[i]);
    }
    sx=(x[1]+x[(n>>1)+1])/2.0;sy=(y[1]+y[(n>>1)+1])/2.0;
    upl=ist(1,2);dwl=ist((n>>1)+1,(n>>1)+2);
    for(int i=2;i<=(n>>1);i++){
        lt[++k1]=ist(i,i+1);
    }
    rt[1]=ist(n,1);
    for(int i=n-1;i>=(n>>1)+2;i--){
        rt[++k2]=ist(i,i+1);
    }
    scanf("%lld",&q);
    int cnt=0;
    while(q--){
        scanf("%lld%lld",&a,&b);
        a^=(cnt*cnt*cnt);b^=(cnt*cnt*cnt);
        if(chk(a,b)){
            puts("Yes");
            cnt++;
        }else{
            puts("No");
        }
    }
}

Comments