CSP2023 考前杂题
前言
今天(9.20)看到了一道有意思的题,便突然有记杂题的想法了。
至于为什么不叫九月杂题呢,毕竟都二十号了嘛。
P6018 [Ynoi2010] Fusion tree
科技题。
首先看到异或就要想到 01Trie,那么考虑如何维护。
假如给每个节点建一个 01Trie 存所有邻居显然是不行的,时间空间双双炸掉,考虑随便定个根,然后存每个结点所有儿子,修改和查询时额外把父亲加上就行了。
然后 01Trie 需要支持插入删除求异或和和整体 $+1$,前三个是简单的。第四个就是这道题需要用科技的地方了。
考虑在二进制上 $+1$ 相当于把最低位的 $0$ 变成 $1$,后面的 $1$ 全变成 $0$。那么假如我们的 01Trie 从低位往高位存储,这个操作就相当于交换结点左右儿子然后向 $0$ 递归。然后稍微注意一下另外三个操作的变化即可。
代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=5e5+5,inf=0x3f3f3f3f;
int n,m,a[N],tg[N];
vector<int> e[N];
struct Trie{
int son[N*22][2],wxor[N*22],num[N*22],root[N],cntn;
int _New(){
++cntn;
son[cntn][0]=son[cntn][1]=0;
wxor[cntn]=0;num[cntn]=0;
return cntn;
}
void init(){cntn=0;forup(i,1,n) root[i]=_New();mem(son,0);}
void _PushUp(int p){
wxor[p]=num[p]=0;
if(son[p][0]){
wxor[p]^=(wxor[son[p][0]]<<1);
num[p]+=num[son[p][0]];
}
if(son[p][1]){
wxor[p]^=((wxor[son[p][1]]<<1)|(num[son[p][1]]&1));
num[p]+=num[son[p][1]];
}
}
void Insert(int p,int a,int q=0){
if(q==21){
++num[p];
return;
}
if(!son[p][a&1]) son[p][a&1]=_New();
Insert(son[p][a&1],a>>1,q+1);
_PushUp(p);
}
void Erase(int p,int a,int q=0){
if(q==21){
--num[p];
return;
}
Erase(son[p][a&1],a>>1,q+1);
_PushUp(p);
}
void Add1(int p,int q=0){
if(q==21) return;
swap(son[p][0],son[p][1]);
if(son[p][0]) Add1(son[p][0],q+1);
_PushUp(p);
}
}mt;
int f[N];
void dfs(int x,int fa){
f[x]=fa;
for(auto i:e[x]){
if(i==fa) continue;
dfs(i,x);
}
}
signed main(){
n=read();m=read();
forup(i,1,n-1){
int u=read(),v=read();
e[u].push_back(v);
e[v].push_back(u);
}
dfs(1,0);
mt.init();
forup(i,1,n){
a[i]=read();
if(i!=1) mt.Insert(mt.root[f[i]],a[i]);
}
forup(Case,1,m){
int op=read();
if(op==1){
int x=read();tg[x]++;
if(x!=1&&f[x]!=1){
int ff=f[x];
mt.Erase(mt.root[f[ff]],a[ff]+tg[f[ff]]);
a[ff]++;
mt.Insert(mt.root[f[ff]],a[ff]+tg[f[ff]]);
}else if(x!=1){
a[f[x]]++;
}
mt.Add1(mt.root[x]);
}else if(op==2){
int x=read(),v=read();
if(x!=1){
mt.Erase(mt.root[f[x]],a[x]+tg[f[x]]);
a[x]-=v;
mt.Insert(mt.root[f[x]],a[x]+tg[f[x]]);
}else{
a[x]-=v;
}
}else{
int x=read(),ans=mt.wxor[mt.root[x]];
if(x!=1) ans^=a[f[x]]+tg[f[f[x]]];
printf("%d\n",ans);
}
}
}
P4198 楼房重建
首先显然是要维护斜率的,后面的大小比较都默认是说斜率了。
那么题意就是单点修改,求前缀最大值数量。
前缀最大值数量不具有结合律,乍一看不能用线段树维护,但是这道题就是要反其道而行。
首先考虑合并时左儿子的前缀最大值必定是整个区间的前缀最大值,那么只用考虑右儿子大于左儿子最大值的部分。
设右儿子为 $u$,左儿子为 $v$,$r_u$ 表示 $u$ 内的前缀最大值个数,$mx_u$ 表示 $u$ 内的最大值,$ls,rs$ 分别代表 $u$ 的左右儿子,那么分情况讨论:
若 $mx_v>mx_u$,右儿子对当前区间的贡献必为 $0$,直接等于左区间的 $r$。
若 $mx_{ls}<mx_v<mx_u$,那么 $ls$ 就没有贡献,递归查找 $rs$。
若 $mx_v<mx_{ls}$,那么 $rs$ 的贡献必定为 $r_u-r_{ls}$,递归查找 $ls$。
那么合并的复杂度就是 $O(\log n)$ 的,总复杂度 $O(n\log^2 n)$。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(i64 i=(s);i<=(e);i++)
#define fordown(i,s,e) for(i64 i=(s);i>=(e);i--)
using namespace std;
using i64=long long;
#define gc getchar()
inline i64 read(){
i64 x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const i64 N=1e5+5,inf=0x3f3f3f3f;
i64 n,m;
struct Node{
i64 x,y;
Node(i64 _x=1,i64 _y=-1):x(_x),y(_y){};
bool operator <(const Node &r)const{return y*r.x<r.y*x;}
bool operator >(const Node &r)const{return y*r.x>r.y*x;}
bool operator <=(const Node &r)const{return y*r.x<=r.y*x;}
bool operator >=(const Node &r)const{return y*r.x>=r.y*x;}
bool operator ==(const Node &r)const{return y*r.x==r.y*x;}
};
struct SegTree{
#define mid ((l+r)>>1)
#define lson l,mid,id<<1
#define rson mid+1,r,id<<1|1
Node querymax[N<<2];
i64 queryans[N<<2];
i64 Getans(Node LMX,i64 l,i64 r,i64 id){
if(queryans[id]==0){
return 0;
}
if(l==r){
return 1;
}
if(LMX<querymax[id<<1]){
return Getans(LMX,lson)+queryans[id]-queryans[id<<1];
}else{
return Getans(LMX,rson);
}
}
void Update(i64 P,Node X,i64 l=1,i64 r=n,i64 id=1){
if(l==r){
querymax[id]=X;
queryans[id]=1;
return;
}
if(P<=mid) Update(P,X,lson);
else Update(P,X,rson);
querymax[id]=max(querymax[id<<1],querymax[id<<1|1]);
if(querymax[id<<1]>=querymax[id<<1|1]){
queryans[id]=queryans[id<<1];
}else if(r==mid+1){
queryans[id]=queryans[id<<1]+queryans[id<<1|1];
}else{
queryans[id]=queryans[id<<1]+Getans(querymax[id<<1],rson);
}
}
i64 Ask(){
return queryans[1];
}
}mt;
signed main(){
n=read();m=read();
forup(Case,1,m){
i64 x=read(),y=read();
mt.Update(x,Node(x,y));
printf("%lld\n",mt.Ask());
}
}
P7470 [NOI Online 2021 提高组] 岛屿探险
本文中 $\oplus$ 表示按位异或。
首先考虑把 $b_i>d_j$ 和 $b_i \le d_j$ 的分开考虑:
对于 $b_i>d_j$ 的,即为求 $a_i\oplus c_j\le d_j$ 的 $i$ 的个数,由于 $c,d$ 是知道的,这个可以直接 01Trie 维护,具体维护方式略。
对于 $b_i\le d_j$ 的,即为求 $c_j\oplus a_i\le b_i$ 的 $i$ 的个数,发现和上一种情况是对称的,那么考虑把询问塞到 01Trie 里面,然后统计改为给 Trie 的结点打标记,最后贡献即为根到叶子路径上标记的综合。
但是假如每次询问都这样做复杂度直接爆炸,大概是 $O(qn\log V)$ 的,那么考虑如何维护多次询问:
首先考虑全都是 $b_i>d_j$ 的(貌似有部分分),可以开一个可持久化 Trie,然后仿照可持久化权值线段树做前缀和即可。
然后假如全是 $b_i\le d_j$,我们可以把询问拆成 $[1,r]-[1,l-1]$,直接离线下来排序做即可。
这里离线下来指的是把所有 $c_j$ 插进 Trie 里,然后排序后遇到 $a_i$ 就打标记,遇到 $c_i$ 就查询路径上的标记和。
然后就转化成了一个偏序问题,直接套一层 CDQ 分治即可。
但是既然已经用了 CDQ 了,那可以把一维偏序当二维偏序做,就不需要可持久化 Trie 了。
复杂度分析:
$$T(n)=2T(\frac{n}{2})+O(n\log V)$$
那么 $T(n)$ 的渐进复杂度即为 $O(n\log n\log V)$,然后这里的 $n$ 取题目中的 $n+q$,所以复杂度即为 $O((n+q)\log(n+q)\log V)$。
参考代码 updated on 22 Sept.
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
using pii=pair<int,int>;
#define fi first
#define se second
#define mkp make_pair
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=1e5+5,inf=0x3f3f3f3f;
int n,m,ans[N];
struct Trie1{
int tag[N*25],son[N*25][2],cntn;
void init(){
mem(tag,0);mem(son,0);cntn=0;
}
void Clear(){
forup(i,0,cntn){
tag[i]=son[i][0]=son[i][1]=0;
}
cntn=0;
}
void Insert(int a){
int p=0;
fordown(i,23,0){
if(!son[p][(a>>i)&1]) son[p][(a>>i)&1]=++cntn;
p=son[p][(a>>i)&1];
}
}
void Work(int a,int b){
int p=0;
fordown(i,23,0){
if((b>>i)&1){
if(son[p][(a>>i)&1]) tag[son[p][(a>>i)&1]]++;
if(son[p][((a>>i)&1)^1]) p=son[p][((a>>i)&1)^1];
else return;
}else{
if(son[p][(a>>i)&1]) p=son[p][(a>>i)&1];
else return;
}
}
tag[p]++;
}
int Get(int a){
int p=0,res=0;
fordown(i,23,0){
res+=tag[p];
p=son[p][(a>>i)&1];
}
res+=tag[p];
return res;
}
}t1;
struct Trie0{
int son[N*25][2],cntn,cnt[N*25];
void init(){
mem(son,0);mem(cnt,0);
cntn=0;
}
void Clear(){
forup(i,0,cntn){
son[i][0]=son[i][1]=cnt[i]=0;
}
cntn=0;
}
void Insert(int a){
int p=0;
fordown(i,23,0){
cnt[p]++;
if(!son[p][(a>>i)&1]) son[p][(a>>i)&1]=++cntn;
p=son[p][(a>>i)&1];
}
cnt[p]++;
}
int Work(int a,int b){
int res=0,p=0;
fordown(i,23,0){
if((b>>i)&1){
if(son[p][(a>>i)&1]) res+=cnt[son[p][(a>>i)&1]];
if(son[p][((a>>i)&1)^1]) p=son[p][((a>>i)&1)^1];
else return res;
}else{
if(son[p][(a>>i)&1]) p=son[p][(a>>i)&1];
else return res;
}
}
res+=cnt[p];
return res;
}
}t0;
struct Node{
int tp,r,f,a,b,pos;
}q[N<<2];
void cdq(int l,int r){
if(l>=r){return;}
int mid=(l+r)>>1;
cdq(l,mid);cdq(mid+1,r);
vector<Node> v0,v1;
t0.Clear();t1.Clear();
forup(i,l,mid){
if(q[i].tp==0) v0.push_back(q[i]);
else v1.push_back(q[i]),t1.Insert(q[i].a);
}
int l0=0,l1=0;
forup(i,mid+1,r){
if(q[i].tp==0){
while(l1<(int)v1.size()&&v1[l1].r<q[i].r){
ans[v1[l1].pos]+=t1.Get(v1[l1].a)*v1[l1].f;
++l1;
}
t1.Work(q[i].a,q[i].b);
}else{
while(l0<(int)v0.size()&&v0[l0].r<=q[i].r){
t0.Insert(v0[l0].a);
++l0;
}
ans[q[i].pos]+=t0.Work(q[i].a,q[i].b)*q[i].f;
}
}
while(l1<(int)v1.size()){
ans[v1[l1].pos]+=t1.Get(v1[l1].a)*v1[l1].f;
++l1;
}
inplace_merge(q+l,q+mid+1,q+r+1,[](Node a,Node b){return a.r<b.r;});
}
signed main(){
n=read();m=read();
t1.init();t0.init();
forup(i,1,n){
q[i].tp=0;q[i].r=i;q[i].a=read();q[i].b=read();
}
forup(i,1,m){
int l=read(),r=read(),c=read(),d=read(),tt=i*2+n-1;
q[tt].tp=q[tt+1].tp=1;
q[tt].a=q[tt+1].a=c;
q[tt].b=q[tt+1].b=d;
q[tt].pos=q[tt+1].pos=i;
q[tt].r=l-1;q[tt].f=-1;
q[tt+1].r=r;q[tt+1].f=1;
}
sort(q+1,q+m*2+n+1,[](Node a,Node b){return a.b>b.b;});
// forup(i,1,m*2+n){
// printf("%d %d %d %d %d %d||\n",q[i].tp,q[i].a,q[i].b,q[i].pos,q[i].r,q[i].f);
// }
cdq(1,m*2+n);
forup(i,1,m){
printf("%d\n",ans[i]);
}
}
P8349 [SDOI/SXOI2022] 整数序列
根号分治题。
题意就是说选一个区间内两种颜色数量相等,最大化权值和。
首先考虑暴力,把两种颜色取出来,设 $x$ 的总数量为 $len_x$,然后从前往后扫一遍,设一个前缀的权值是 $c_x-c_y+len_y$($c_x$ 表示前缀中 $x$ 的个数,加上 $len_y$ 是为了防止负数下标),那么容易发现两个全职相同的前缀的差就是一个合法的区间,后面的维护是简单的。
复杂度为 $O(len_x+len_y)$。
设一个阈值 $K$,然后把 $len_x>K$ 的称为“大色”,$len_x\le K$ 的称为“小色”,那么可以把询问分为三种:
- 小色对小色
直接暴力复杂度是 $O(K)$ 的,复杂度最多是 $O(qK)$。
- 大色对大色
这样的颜色最多有 $\frac{n}{K}$ 种,本质不同的对数只有 $\frac{n}{K}^2$ 对,可以用 unordered_map 存起来。设有 $k$ 个大色,极限情况下 $\sum_{i=1}^k {len_i}=n$,那么共有 $\frac{k(k-1)}{2}$ 种本质不同的询问,总计算次数为 $\sum_{i\le i<j\le k}{len_i+len_j}=(k-1)\sum_{i=1}^k{len_i}=n(k-1)$。由于 $len_i\le K$,得到 $k\le \frac{n}{K}$,则极限复杂度为 $O(\frac{n^2}{K})$。
当然也可以感性理解,此处给了严谨证明就略过了。
- 大色对小色
由于小色对应的点数和大色对应的点数差距悬殊,而题目要求选择的区间内两种颜色点数相同,大色里面有很多点都是不可能产生贡献的的。我们可以把两种颜色的点分成有效点与无效点两种。
为方便叙述,假设 $len_x\le K <len_y$
首先 $x$ 内所有点都是有效点(显然吧)。
然后考虑维护 $y$ 内有效点的集合,遍历 $x$,然后二分对应的下一个 $y$,这样也能找到一段极长的连续 $x$,设这一段的长度为 $l$,那么往前 $l$ 个 $y$,往后 $l$ 个 $y$ 都是有效点,然后注意跳过原本就是有效点的,这里可以用 set 维护,容易发现一个 $x$ 会对应至多 $2$ 个 $y$,故有效点的数量是 $O(K)$ 的,那么就可以直接暴力了。复杂度是 $O(len_x\log{len_y})$
考虑极限情况,设有 $k_1$ 个大色,其中第 $i$ 个大小为 $L_i$,有 $k_2$ 个小色,其中第 $i$ 个大小为 $l_i$,考虑到复杂度与小色的大小关系更大,那么我们用最大的 $\frac{q}{k_1}$ 个小色对大色询问,这样对于记忆化是最劣的,计算次数为 $\sum_{i=1}^{k_2}\sum_{j=1}^{k_1}l_i\log L_j\le k_1\log n\sum l_i$。
最强的情况,可以构造出约为 $\frac{n}{2K}$ 个长度略大于 $K$ 的大色,然后其余小色总长度约为 $\frac{n}{2}$,并且使每个大色对每个小色问一遍,此时 $k_1$ 约为 $O(\frac{n}{K})$,$\sum l_i$ 约为 $O(n)$,则总复杂度为 $\frac{n^2\log n}{B}$。
总复杂度约为 $O(qK+\frac{n^2\log n}{K})$,大对大的因为严格小于大对小可以直接忽略,据说 $K$ 取 $\sqrt{\frac{n^2\log n}{q}}$ 时最优,但是我个人觉得取 $\sqrt{n}$ 差不多得了( 主要是我不会证明 )。
好了现在我会证了,感谢 xx019。
根据均值不等式 $a+b\ge 2\sqrt{ab}$,$qK+\frac{n^2\log n}{K}\ge 2\sqrt{qn^2\log n}$,且在 $qK=\frac{n^2\log n}{K}$ 时取等,即 $K=\sqrt{\frac{n^2\log n}{q}}$,此时复杂度为 $O(n\sqrt{q\log n})$。
好了写出来了,$O(n\sqrt{q\log n})$ 没卡过去,学了下 $O(n\sqrt{q})$ 的写法。
具体来说,把大色对小色的离线到大色上,然后对于每个大色 $y$ 可以 $O(n)$ 预处理序列上每个数往前第一个 $y$ 和往后第一个 $y$。然后用栈维护连续段的个数,假如当前段的左端点比上一段右端点靠前就可以合并,再前缀和维护一下合并时没产生贡献的点数,把工薪额外加在当前区间的两端,最后和前面的做法一样,总的来说压掉了一个 $\sqrt{\log}$,就不用卡常了。
参考代码 updated on 22 Sept.
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
using pii=pair<int,int>;
#define fi first
#define se second
#define mkp make_pair
using i64=long long;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=3e5+5,TT=300;
const i64 inf=1e18;
int n,q,a[N],b[N];
vector<int> pos[N];
i64 bkt[N],ans[1000005];
unordered_map<int,i64> mp[N];
vector<pii> quu[N];
int pre[N],nxt[N],cnt[N];
i64 calc(vector<int> &t1,vector<int> &t2){
int l1=0,l2=0,sz=t1.size()+t2.size();
forup(i,0,sz) bkt[i]=inf;
int nw=t2.size();i64 res=-inf,sum=0;
bkt[nw]=0;
forup(i,1,sz){
if(l1<(int)t1.size()&&(l2>=(int)t2.size()||t2[l2]>t1[l1])){
++nw;
sum+=b[t1[l1]];
res=max(res,sum-bkt[nw]);
bkt[nw]=min(bkt[nw],sum);
++l1;
}else{
--nw;
sum+=b[t2[l2]];
res=max(res,sum-bkt[nw]);
bkt[nw]=min(bkt[nw],sum);
++l2;
}
}
return res;
}
int id[N],ps[N];
signed main(){
// freopen("ex_sequence2.in","r",stdin);
// freopen("a.out","w",stdout);
n=read();q=read();
forup(i,1,n){
a[i]=read();
pos[a[i]].push_back(i);
}
forup(i,1,n){
b[i]=read();
}
forup(Case,1,q){
int x=read(),y=read();
if(pos[x].size()>pos[y].size()||(pos[x].size()==pos[y].size()&&x>y)) swap(x,y);
if(mp[x].count(y)){
ans[Case]=mp[x][y];
continue;
}
if((pos[x].size()<=TT&&pos[y].size()<=TT)||(pos[x].size()>TT&&pos[y].size()>TT)){
mp[x][y]=ans[Case]=calc(pos[x],pos[y]);
}else{
quu[y].push_back(mkp(Case,x));
}
}
forup(y,1,n){
if(pos[y].size()<=TT) continue;
forup(i,1,n) pre[i]=(a[i]==y?i:pre[i-1]);
forup(i,1,n) cnt[i]=cnt[i-1]+(a[i]==y);
nxt[n+1]=n+1;cnt[n+1]=cnt[n];
fordown(i,n,1) nxt[i]=(a[i]==y?i:nxt[i+1]);
ps[1]=0;id[0]=1;
int cn=1;
forup(i,1,n){
if(a[i]==y){
id[i]=++cn;
ps[cn]=i;
}
}
id[n+1]=++cn;
ps[cn]=n+1;
for(auto i:quu[y]){
vector<pii> stk;
int x=i.se,pp=i.fi;
if(mp[x].count(y)){
ans[pp]=mp[x][y];
continue;
}
for(auto j:pos[x]){
pii nw=mkp(pre[j],nxt[j]);
while(stk.size()&&stk.back().se>=nw.fi){
pii tp=stk.back();stk.pop_back();
if(tp.fi<nw.fi) swap(nw.fi,tp.fi);
if(tp.se>nw.se) swap(nw.se,tp.se);
int num=cnt[tp.se]-(tp.fi?cnt[tp.fi-1]:0);
nw.fi=ps[max(id[nw.fi]-num,1)];
nw.se=ps[min(id[nw.se]+num,cn)];
}
stk.push_back(nw);
}
vector<int> v1;
int l=2;
for(auto j:stk){
int st=j.fi,ed=j.se;
if(l<id[st]-1) l=id[st]-1;
while(l<cn&&l<=id[ed]+1){
v1.push_back(ps[l++]);
}
}
mp[x][y]=ans[pp]=calc(pos[x],v1);
}
}
forup(i,1,q){
printf("%lld\n",ans[i]);
}
}
P7739 [NOI2021] 密码箱
首先 $f(a)$ 相当于重复 $n-1$ 次把末项取倒数然后加在倒数第二项里再删掉这一项,设现在的末项为 $\frac{x}{y}$,倒数第二项为 $a_{n-1}$,容易发现假如 $\gcd(x,y)=1$,那么 $\gcd(y+a_{n-1}x,x)=1$(即加入下一项后的分子分母),又由于最开始 $y=1$,所以其实并不需要约分,那么只用考虑取模即可。
容易想到 $x,y$ 可以用矩阵乘法维护,先不考虑三种操作,假设序列 $a$ 固定,我们先把矩阵构造出来:
具体的,我们希望构造的矩阵 $A_i$ 满足以下式子:
$$A_i\times \begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}y+a_ix\\x\end{bmatrix}$$
由于每次是乘最后一个所以我设置为把一个列向量乘在右边,这样每次加入新的操作就是乘在右边的,比较符合直觉。
那么解一解方程,容易发现矩阵 $A_i$ 应该长这样:
$$\begin{bmatrix}a_i&1\\1&0\end{bmatrix}$$
但是现在 W,E 两种操作还是不好维护,我们希望这两种操作也能用矩阵概括。
首先是 W,我们设它对应的矩阵为 $W$,那么我们希望它满足以下式子:
$$\begin{bmatrix}b&1\\1&0\end{bmatrix}\times W=\begin{bmatrix}b+1&1\\1&0\end{bmatrix}$$
然后解一解方程可以发现:
$$W=\begin{bmatrix}1&0\\1&1\end{bmatrix}$$
但是对于 E 操作仍然不好维护,但是假如我们发现对于 $a_n=1$,E 的两种操作类型对答案的影响相同的话,就能维护了,记住,转换题意后一定记得回到原题意解题。
由于只要后面的一样就肯定肯定不影响前面的,我们不妨假设现在后面的算出来是 $\frac{x}{y}$,然后前面啥也没有,那么可以简单推一下:
- 给倒数第二项加一。
$$ \begin{aligned} f(a_1+1,1,\frac{x}{y}) =&f(a_1+1,\frac{x+y}{x})\\ =&f(\frac{(a_1+1)(x+y)+x}{x+y})\\ =&\frac{a_1(x+y)+2x+y}{x+y} \end{aligned} $$
- 给最后一项减一,然后添两个 $1$
$$ \begin{aligned} f(a_1,0,1,1,\frac{x}{y}) =&f(a_1,0,1,\frac{x+y}{x})\\ =&f(a_1,0,\frac{2x+y}{x+y})\\ =&f(a_1,\frac{x+y}{2x+y})\\ =&f(\frac{a_1(x+y)+2x+y}{x+y})\\ =&\frac{a_1(x+y)+2x+y}{x+y} \end{aligned} $$
显然这两个东西相等,那么 E 操作实际上就是:先给数列的最后一项减 $1$,接着在数列尾再加两项,两项的值都是 $1$。
那么仿照刚才算 $W$(真的仿了吗?如仿),$E$ 的矩阵如下:
$$E=\begin{bmatrix}1&0\\-1&1\end{bmatrix}\times\begin{bmatrix}1&1\\1&0\end{bmatrix}\times \begin{bmatrix}1&1\\1&0\end{bmatrix}=\begin{bmatrix}2&1\\-1&0\end{bmatrix}$$
好了,现在我们已经会维护 APPEND 操作了,✿✿ヽ(°▽°)ノ✿。
那么区间翻转和区间反转操作呢?首先翻转操作可以考虑文艺平衡树维护,但是反转操作呢?
其实是一样的,我们对于每个子树预处理当前矩阵,操作反转的矩阵,操作翻转的矩阵,操作翻转后反转的矩阵。然后和文艺平衡树一样打标记维护,每次下传标记就 swap 一下即可。复杂度 $O((n+q)\log (n+q)2^3)$。
最后考虑一下如何求答案,设最后整个操作序列乘出来的矩阵为 $B$,那么首先在前面乘上初始的两个数(这个很简单),考虑后面乘的一个初始向量是多少,设这个向量为 $V$,那么我们希望:
$$\begin{bmatrix}a_i&1\\1&0\end{bmatrix}\times V=\begin{bmatrix}a_i\\1\end{bmatrix}$$
容易得到:
$$V=\begin{bmatrix}1\\0\end{bmatrix}$$
所以最终答案为:
$$ \begin{aligned} &A_0\times A_1\times B\times V\\ =&\begin{bmatrix}1&0\\1&1\end{bmatrix}\times B\times \begin{bmatrix}1\\0\end{bmatrix} \end{aligned} $$
然后总结一下,以后看到很难维护的操作应该考虑一下能不能转化成矩阵乘法。
参考代码 updated on 22 Sept.
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=2e5+5,inf=0x3f3f3f3f,mod=998244353;
int n,q;
char str[N];
void adm(int &a,int b){
a+=b;
if(a>=mod) a-=mod;
if(a<0) a+=mod;
}
struct Matrix{
int c[2][2];
Matrix(int _=1,int __=0,int ___=0,int ____=1){
c[0][0]=_;
c[0][1]=__;
c[1][0]=___;
c[1][1]=____;
}
Matrix operator *(const Matrix &b){
Matrix res(0,0,0,0);
forup(i,0,1){
forup(j,0,1){
forup(k,0,1){
adm(res.c[i][j],1ll*c[i][k]*b.c[k][j]%mod);
}
}
}
return res;
}
}W(1,0,1,1),E(2,1,-1,0);
mt19937 mr(time(0));
struct FHQTreap{
private:
int ls[N],rs[N],sz[N],root,cntn,hv[N];
bool tv[N],itag[N],rtag[N];// true->E false->W
Matrix ori[N],rev[N],inv[N],rinv[N];
int _New(bool val){
int id=++cntn;
tv[id]=val;
Matrix p=W,q=E;
if(val) swap(p,q);
ori[id]=rev[id]=p;
inv[id]=rinv[id]=q;
sz[id]=1;
ls[id]=rs[id]=0;
itag[id]=rtag[id]=0;
hv[id]=mr();
return id;
}
void _PushUp(int id){
Matrix p=W,q=E;
if(tv[id]) swap(p,q);
sz[id]=sz[ls[id]]+1+sz[rs[id]];
ori[id]=ori[ls[id]]*p*ori[rs[id]];
inv[id]=inv[ls[id]]*q*inv[rs[id]];
rev[id]=rev[rs[id]]*p*rev[ls[id]];
rinv[id]=rinv[rs[id]]*q*rinv[ls[id]];
}
void _Reverse(int id){
swap(ls[id],rs[id]);
swap(ori[id],rev[id]);
swap(inv[id],rinv[id]);
}
void _Inverse(int id){
tv[id]^=1;
swap(ori[id],inv[id]);
swap(rev[id],rinv[id]);
}
void _PushDown(int id){
if(itag[id]){
if(ls[id]) _Inverse(ls[id]),itag[ls[id]]^=1;
if(rs[id]) _Inverse(rs[id]),itag[rs[id]]^=1;
itag[id]=0;
}
if(rtag[id]){
if(ls[id]) _Reverse(ls[id]),rtag[ls[id]]^=1;
if(rs[id]) _Reverse(rs[id]),rtag[rs[id]]^=1;
rtag[id]=0;
}
}
void _Split(int key,int id,int &x,int &y){
if(!id){
x=y=0;
return;
}
_PushDown(id);
if(sz[ls[id]]<key){
x=id;
_Split(key-sz[ls[id]]-1,rs[id],rs[x],y);
}else{
y=id;
_Split(key,ls[id],x,ls[y]);
}
_PushUp(id);
}
int _Merge(int x,int y){
if(!x||!y) return x|y;
if(hv[x]>hv[y]){
_PushDown(x);
rs[x]=_Merge(rs[x],y);
_PushUp(x);
return x;
}else{
_PushDown(y);
ls[y]=_Merge(x,ls[y]);
_PushUp(y);
return y;
}
}
public:
FHQTreap():root(0),cntn(0){}
void Insert(char c){
root=_Merge(root,_New(c=='E'));
}
void Inverse(int l,int r){
int x,y,z;
_Split(l-1,root,x,y);_Split(r-l+1,y,y,z);
_Inverse(y);itag[y]^=1;
root=_Merge(_Merge(x,y),z);
}
void Reverse(int l,int r){
int x,y,z;
_Split(l-1,root,x,y);_Split(r-l+1,y,y,z);
_Reverse(y);rtag[y]^=1;
root=_Merge(_Merge(x,y),z);
}
Matrix Ask(){
return ori[root];
}
}mt;
signed main(){
n=read();q=read();
scanf(" %s",str+1);
forup(i,1,n){
mt.Insert(str[i]);
}
Matrix ans=Matrix(1,0,1,1)*mt.Ask()*Matrix(1,0,0,0);
printf("%d %d\n",ans.c[0][0],ans.c[1][0]);
forup(Case,1,q){
scanf(" %s",str+1);
if(str[1]=='A'){
char c;
scanf(" %1c",&c);
mt.Insert(c);
}else if(str[1]=='F'){
int l=read(),r=read();
mt.Inverse(l,r);
}else{
int l=read(),r=read();
mt.Reverse(l,r);
}
Matrix ans=Matrix(1,0,1,1)*mt.Ask()*Matrix(1,0,0,0);
printf("%d %d\n",ans.c[0][0],ans.c[1][0]);
}
}
P7518 [省选联考 2021 A/B 卷] 宝石
设查询的路径为 $u,v$,且 $\mathrm{lca}(u,v)=t$,那么我们可以把每个询问分成 $u\to t,t\to v$ 三部分。
首先 $u\to t$ 的,这是一段上升的路径,那么我们可以利用倍增跳,具体地,设 $f_{u,i}$ 表示从 $u$ 开始,从 $w_u$ 的后继开始只向上走收集 $2^i$ 个宝石后到达哪个结点,预处理一下 $f_{u,0}$,然后后面就是正常倍增了。
然后考虑 $t\to v$,我们可以把所有询问以二元组 $(c_i,i)$ 离线到 $t$ 上,然后在 $v$ 处打一个结束标记,表示编号为 $i$ 的询问在 $t$ 之前拿到的最后一个宝石为 $c_i$,这里我们需要对每个宝石维护一个容器 $d_c$,表示该容器内所有询问的下一颗宝石为 $c$,这个容器需要以下功能:
- 在进入结点 $k$ 时,将所有 $i$ 插入 $d_{c_i}$ 中。
- 将 $w_k$ 和 $w_k$ 的后继合并。
- 对于所有结束标记,查询所在容器。
- 在退出结点 $k$ 时,撤销所有操作。
显然,可以用可撤销并查集维护,复杂度 $O(q\log n+n\log q)$。
参考代码 updated on 25 Sept.
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=2e5+5,M=5e4+5,inf=0x3f3f3f3f;
int n,m,c,q,w[N],ans[N];
vector<int> e[N];
struct query{
int pos,cc;
};
int p[M],pre[M],nxt[M];
vector<query> st[N];
vector<int> ed[N];
int f[N][19],dpt[N],f2[N][19],nw[M],tst[N];
int cntc[N];
void dfs(int x,int fa){
dpt[x]=dpt[fa]+1;f[x][0]=fa;
forup(i,1,18){f[x][i]=f[f[x][i-1]][i-1];}
f2[x][0]=nw[nxt[w[x]]];
forup(i,1,18){f2[x][i]=f2[f2[x][i-1]][i-1];}
int sv=nw[w[x]];nw[w[x]]=x;
tst[x]=nw[p[1]];
for(auto i:e[x]){
if(i==fa) continue;
dfs(i,x);
}
nw[w[x]]=sv;
}
int lca(int x,int y){
if(dpt[x]>dpt[y]) swap(x,y);
for(int i=18;dpt[y]>dpt[x]&&i>=0;--i){
if(dpt[f[y][i]]>=dpt[x]) y=f[y][i];
}
if(x==y) return x;
for(int i=18;f[x][0]!=f[y][0]&&i>=0;--i){
if(f[x][i]!=f[y][i]){
x=f[x][i];y=f[y][i];
}
}
return f[x][0];
}
int fa[N],sz[N],mp[N],co[N];
struct Node{
int u,v,cu,cv;
};
stack<Node> stk;
int getfa(int x){return x==fa[x]?x:getfa(fa[x]);}
void merge(int u,int v){
int fu=getfa(u),fv=getfa(v);
if(fu==fv) return;
int nv=co[fv],nu=co[fu];
if(sz[fu]>sz[fv]) swap(fu,fv);
stk.push(Node{fu,fv,co[fu],co[fv]});
sz[fv]+=sz[fu];
fa[fu]=fv;
co[fv]=nv;
mp[nu]=0;mp[nv]=fv;
}
void ctrlz(){
int fu=stk.top().u,fv=stk.top().v,cu=stk.top().cu,cv=stk.top().cv;stk.pop();
if(fv) co[fv]=cv,sz[fv]-=sz[fu];
mp[co[fu]]=0;
if(cu) mp[cu]=fu;
if(cv) mp[cv]=fv;
fa[fu]=fu;
co[fu]=cu;
}
void dfs2(int x,int fa){
int ppp=stk.size();
for(auto i:st[x]){
if(mp[i.cc]==0){
mp[i.cc]=i.pos;
co[i.pos]=i.cc;
stk.push(Node{i.pos,0,0,0});
}else{
merge(i.pos,mp[i.cc]);
}
}
if(mp[w[x]]){
if(mp[nxt[w[x]]]){
merge(mp[w[x]],mp[nxt[w[x]]]);
}else{
stk.push(Node{mp[w[x]],0,w[x],0});
co[mp[w[x]]]=nxt[w[x]];
mp[nxt[w[x]]]=mp[w[x]];
mp[w[x]]=0;
}
}
for(auto i:ed[x]){
int nc=co[getfa(i)];
ans[i]=cntc[nc]-1;
}
for(auto i:e[x]){
if(i==fa) continue;
dfs2(i,x);
}
while((int)stk.size()>ppp){
ctrlz();
}
}
signed main(){
n=read();m=read();c=read();
forup(i,1,c){
p[i]=read();
nxt[p[i-1]]=p[i];
pre[p[i]]=p[i-1];
cntc[p[i]]=cntc[p[i-1]]+1;
}
p[c+1]=m+1;
nxt[p[c]]=m+1;
cntc[m+1]=c+1;
forup(i,1,n) w[i]=read();
forup(i,1,n-1){
int u=read(),v=read();
e[u].push_back(v);
e[v].push_back(u);
}
dfs(1,0);
q=read();
forup(Case,1,q){
int u=read(),v=read(),y=lca(u,v);
int l=tst[u];
if(dpt[l]<dpt[y]){
st[y].push_back(query{Case,p[1]});
ed[v].push_back(Case);
}else{
fordown(i,18,0){
if(dpt[f2[l][i]]>=dpt[y]){
l=f2[l][i];
}
}
if(w[l]==p[c]) ans[Case]=c;
else st[y].push_back(query{Case,nxt[w[l]]}),ed[v].push_back(Case);
}
}
forup(i,1,q){
fa[i]=i;sz[i]=1;
}
dfs2(1,0);
forup(i,1,q){
printf("%d\n",ans[i]);
}
}
CF1017G The Tree
首先,直接做要么修改是 $O(n)$ 的(暴力修改,单点查询),要么查询是 $O(n)$ 的(标记修改,往上跳查询),其中一个会被链卡另一个会被菊花图卡。
那么我们可以考虑均衡一下,让修改和查询都变成 $O(\sqrt{n})$ 的,很自然地想到分块。
思路是将询问分成 $\sqrt{q}$ 块,对于每一块建虚树,然后处理完一块后用虚树上的信息给原树染色。
这样要求块内每个操作复杂度不多于 $O(\sqrt{n})$,对每一块预处理和处理完一块后染色的复杂度不多于 $O(n)$。
首先是建虚树,但是为了维护操作 $1$ 需要处理虚树上每个关键点和它父亲中间有多少个白点,由于反正都要维护链的信息了,那直接可以 $O(n)$ 建虚树,符合条件。
然后是三个操作,操作 $3$ 直接查即可,操作 $1$ 维护一下每条边上剩的白点数,假如全涂完了就往儿子递归,由于点数不超过 $\sqrt{q}$ 所以复杂度是对的,为了后面染回原树可能要维护一下每条边加了几个黑点,有没有被涂白过。操作 $2$ 就直接遍历,三个操作复杂度均不超过 $O(\sqrt{q})$。
然后是染色,我现在臆想的实现是遍历虚树,然后每次定位到原树的这个结点,分有没有涂白过把距离最近的若干个白点涂黑,或者把黑点刷白,复杂度是 $O(\sqrt{q}+n)$ 的。
然后就做完了,估计代码不会太好写。
参考代码 updated on 27 Sept.
其实还挺好写的,就是调到一半 CF 炸了被迫去写下一题。
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=1e5+5,P=350;
int n,m,ans[N],op[N];
vector<int> e[N],e1[N];
struct operation{
int op,x;
}q[N];
int f[N][21],dpt[N],st[N],Tm,co[N];
void dfs1(int x,int fa){
st[x]=++Tm;
f[x][0]=fa;dpt[x]=dpt[fa]+1;
forup(i,1,20){
f[x][i]=f[f[x][i-1]][i-1];
}
for(auto i:e[x]){
if(i==fa) continue;
dfs1(i,x);
}
}
int lca(int x,int y){
if(dpt[x]>dpt[y]) swap(x,y);
for(int i=20;i>=0&&dpt[y]>dpt[x];--i){
if(dpt[f[y][i]]>=dpt[x]){
y=f[y][i];
}
}
if(x==y) return x;
for(int i=20;i>=0&&f[x][0]!=f[y][0];--i){
if(f[x][i]!=f[y][i]){
x=f[x][i];y=f[y][i];
}
}
return f[x][0];
}
int ispt[N],ctw[N],isw[N],vc[N],ff[N],cntb[N];
void dfs2(int x,int fa,int nc,int pre){
if(ispt[x]){
e1[x].push_back(pre);
e1[pre].push_back(x);
ff[x]=pre;
ctw[x]=nc;nc=0;
pre=x;
vc[x]=co[x];
}
if(!co[x]) ++nc;
for(auto i:e[x]){
if(i==fa) continue;
dfs2(i,x,nc,pre);
}
}
void dfs3(int x,int fa,int tp){
if(tp==0){
vc[x]=0;isw[x]=1;
cntb[x]=0;
for(auto i:e1[x]){
if(i==fa) continue;
ctw[i]=dpt[i]-dpt[x];
dfs3(i,x,0);
}
}else{
cntb[x]++;
if(vc[x]){
for(auto i:e1[x]){
if(i==fa) continue;
if(cntb[x]>ctw[i]){
dfs3(i,x,1);
}
}
}else{
vc[x]=1;
}
}
}
void dfs4(int x,int fa,int cb,int iw){
if(ispt[x]){
if(isw[x]) iw=1;
cb=cntb[x];
}
if(iw){
if(cb){
co[x]=1;--cb;
}else{
co[x]=0;
}
}else{
if(!co[x]&&cb){
co[x]=1;--cb;
}
}
for(auto i:e[x]){
if(i==fa) continue;
dfs4(i,x,cb,iw);
}
}
void solve(int l,int r){
vector<int> vec;
forup(i,l,r){
vec.push_back(q[i].x);
}
sort(vec.begin(),vec.end(),[](int a,int b){
return st[a]<st[b];
});
vec.erase(unique(vec.begin(),vec.end()),vec.end());
int pp=0;
for(auto i:vec){
ispt[i]=1;
if(pp) ispt[lca(i,pp)]=1;
pp=i;
}
ispt[1]=1;
dfs2(1,0,0,0);
forup(i,l,r){
if(q[i].op==3){
ans[i]=vc[q[i].x];
}else if(q[i].op==2){
dfs3(q[i].x,ff[q[i].x],0);
}else{
dfs3(q[i].x,ff[q[i].x],1);
}
}
dfs4(1,0,0,0);
mem(isw,0);mem(cntb,0);mem(ctw,0);mem(ispt,0);mem(vc,0);mem(ff,0);
forup(i,1,n){
e1[i].clear();
}
}
signed main(){
n=read();m=read();
forup(i,2,n){
int u=read();
e[i].push_back(u);
e[u].push_back(i);
}
forup(i,1,m){
op[i]=q[i].op=read();q[i].x=read();
}
dfs1(1,0);
int cpcp=m/P;
forup(i,1,cpcp){
int L=(i-1)*P+1,R=i*P;
solve(L,R);
}
if(cpcp*P!=m){
int L=cpcp*P+1,R=m;
solve(L,R);
}
forup(i,1,m){
if(op[i]==3){
puts(ans[i]?"black":"white");
}
}
}
CF573E Bear and Bowling
首先有个 $O(n^2)$ DP。
设 $dp_{i,j}$ 表示考虑前 $i$ 个,已经选了 $j$ 个能得到的最大值,转移是简单的:
$$dp_{i,j}=\max(dp_{i-1,j},dp_{i-1,j-1}+a_i\times j)$$
然后这道题由于是 CF 的,考虑到 Java Python 等常数较大的语言,时限开的巨大无比,已经可以日过去了。
但是我可不是那种不求甚解的人呐。
但是这道题还有爆踩标算的 $O(n)$ 贪心做法。可惜这是数据结构专题……
这个方程看起来不太好优化,那么我们考虑猜结论:
$\forall i,\exists k\in[1,i]$,满足:
$$\forall j<k,dp_{i,j}=dp_{i-1,j}$$
$$\forall j\ge k,dp_{i,j}=dp_{i-1,j-1}+a_i\times j$$
就是说前一半是第一种转移,后一半是第二种转移。具体猜法是考虑画图,从 $dp_i\to dp_{i+1}$ 来看,以 $j$ 为横坐标,DP 值为纵坐标,第一种转移就是原地不动,第二种转移相当于向右平移一位再把每个斜率加 $a_i$,然后每个横坐标取纵坐标较大值。从 $i=1$ 随便画一画容易发现很难搞出反例。
证明:
从刚刚猜想的过程容易发现和斜率相关,考虑对 $dp_i$ 构造一个差分序列 $f_i$,其中 $f_{i,j}=dp_{i,j}-dp_{i,j-1}$,设 $i-1\to i$ 转移时的分界点为 $k_i$。
若猜想成立,则有 $dp_{i,k_i-1}\ge dp_{i-1,k_i-2}+a_i\times (k_i-1)$,且 $dp_{i-1,k_i}<dp_{i-1,k_i-1}+a_i\times k_i$,于是 $\frac{f_{i-1,k_i-1}}{k_i-1}\ge a_i$,且 $\frac{f_{i-1,k_i}}{k_i}<a_i$。
容易发现前式对于所有 $j< k_i$ 均成立,后式对于所有 $j\ge k_i$ 均成立,而 $a_i$ 是一个定值,那么若 $\frac{f_{i-1,j}}{j}$ 关于 $j$ 单调不增,则猜想必定成立(对于边界情况,考虑假如 $\frac{f_{i-1,j}}{j}$ 全都小于 $a_i$ 那么 $k_i$ 取 $1$,假如全都大于等于 $a_i$ 那么 $k_i$ 取 $i$)。
若猜想成立,那么由 $dp_i$ 的值可知:
$$\forall j< k_i,f_{i,j}=f_{i-1,j}$$ $$\forall j> k_i,f_{i,j}=f_{i-1,j-1}+a_i$$ $$f_{i,k_i}=a_i\times k_i$$
证明考虑数学归纳法。
首先对于 $i=1$, $\frac{f_{i,j}}{j}$ 显然单调不增(长度为 $1$ 的序列显然单调不增吧)。
于是对于 $i=2$,有 $\frac{f_{i-1,j}}{j}$ 单调不增。
对于更大的数,考虑若猜想成立,证明 $\frac{f_{i,j}}{j}$ 单调不增,即证对于 $i+1$ 猜想成立。
首先对于 $j<k_i$,$f_{i,j}=f_{i-1,j}$,显然单调不增。
对于 $j=k_i$,由于 $\forall j<k_i,\frac{f_{i,j}}{j}=\frac{f_{i-1,j}}{j}\ge a_i$,且 $\frac{f_{i,k_i}}{k_i}=\frac{a_i\times k_i}{k_i}=a_i$,单调性仍然存在。
对于 $j>k_i$:
首先结论长这样:
$$\frac{f_{i,j-1}}{j-1}\ge\frac{f_{i,j}}{j}$$
考虑 $f_{i,j-1}=f_{i-1,j-2}+a_i,f_{i,j}=f_{i-1,j-1}+a_i$。
那么上不等式等价于:
$$ \begin{aligned} \frac{f_{i-1,j-2}+a_i}{j-1}&\ge\frac{f_{i-1,j-1}+a_i}{j}\\ f_{i-1,j-2}+a_i&\ge\frac{j-1}{j}(f_{i-1,j-1}+a_i)\\ f_{i-1,j-2}+a_i&\ge\frac{j-1}{j}f_{i-1,j-1}+\frac{j-1}{j}a_i\\ f_{i-1,j-2}&\ge\frac{j-1}{j}f_{i-1,j-1}-\frac{1}{j}a_i\\ \end{aligned} $$
由于 $\frac{f_{i-1,j}}{j}\ge\frac{f_{i-1,j+1}}{j+1}$,那么 $f_{i-1,j}\ge \frac{j}{j+1}f_{i-1,j+1}$,所以 $f_{i-1,j-2}\ge\frac{j-2}{j-1}f_{i-1,j-1}$,那么左式减右式,得:
$$ \begin{aligned} &f_{i-1,j-2}-(\frac{j-1}{j}f_{i-1,j-1}-\frac{1}{j}a_i)\\ \ge&\frac{j-2}{j-1}f_{i-1,j-1}-(\frac{j-1}{j}f_{i-1,j-1}-\frac{1}{j}a_i)\\ =&\frac{\left[j(j-2)-(j-1)^2\right]f_{i-1,j-1}+(j-1)a_i}{j(j-1)}\\ =&\frac{(j-1)a_i-f_{i-1,j-1}}{j(j-1)}\\ \end{aligned} $$
由于 $j>k_i$,则 $j-1\ge k_i$,那么 $\frac{f_{i-1,j-1}}{j-1}< a_i$(见前文),故 $(j-1)a_i-f_{i-1,j-1}>0$,则上式 $\ge0$。
故 $\frac{f_{i,j-1}}{j-1}\ge\frac{f_{i,j}}{j}$。
那么我们已经证出这个性质了,这个性质有什么用呢?考虑我们之前的推论:
$$\forall j< k_i,f_{i,j}=f_{i-1,j}$$ $$\forall j> k_i,f_{i,j}=f_{i-1,j-1}+a_i$$ $$f_{i,k_i}=a_i\times k_i$$
容易发现 $f_i$ 相当于前半部分继承 $f_{i-1}$,中间插入一个 $a_i\times k_i$,后半部分整体加上 $a_i$。
容易发现这是文艺平衡树能维护的信息,而且 $k_i$ 可以二分找到,那么直接闭着眼睛拍一棵文艺平衡树不就完了吗。
求出差分序列后,最后累加一下即可。
复杂度 $O(n\log n)$。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(i64 i=(s);i<=(e);i++)
#define fordown(i,s,e) for(i64 i=(s);i>=(e);i--)
using namespace std;
using i64=long long;
#define gc getchar()
inline i64 read(){
i64 x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const i64 N=1e5+5;
i64 n,a[N];
mt19937 mr(time(0));
i64 seq[N],cs;
struct FHQTreap{
private:
i64 ls[N],rs[N],tv[N],hv[N],sz[N],cntn,mark[N],root;
i64 _New(i64 val){
i64 nw=++cntn;
ls[nw]=rs[nw]=0;
tv[nw]=val;hv[nw]=mr();
sz[nw]=1;
return nw;
}
void _PushUp(i64 id){
sz[id]=sz[ls[id]]+sz[rs[id]]+1;
}
void _PushDown(i64 id){
if(!mark[id]) return;
tv[ls[id]]+=mark[id];
tv[rs[id]]+=mark[id];
mark[ls[id]]+=mark[id];
mark[rs[id]]+=mark[id];
mark[id]=0;
}
void _Split(i64 id,i64 key,i64 &x,i64 &y,i64 pres){
if(!id){
x=y=0;
return;
}
_PushDown(id);
if(tv[id]<key*(pres+sz[ls[id]]+1)){
y=id;
_Split(ls[id],key,x,ls[y],pres);
}else{
x=id;
_Split(rs[id],key,rs[x],y,pres+sz[ls[id]]+1);
}
_PushUp(id);
}
i64 _Merge(i64 x,i64 y){
if(!x||!y) return x|y;
if(hv[x]>hv[y]){
_PushDown(x);
rs[x]=_Merge(rs[x],y);
_PushUp(x);
return x;
}else{
_PushDown(y);
ls[y]=_Merge(x,ls[y]);
_PushUp(y);
return y;
}
}
void _Calc(i64 id){
_PushDown(id);
if(ls[id]) _Calc(ls[id]);
seq[++cs]=tv[id];
if(rs[id]) _Calc(rs[id]);
}
public:
FHQTreap():cntn(0),root(0){}
void Insert(i64 ai){
i64 x,y;
_Split(root,ai,x,y,0);
if(y){
tv[y]+=ai;mark[y]+=ai;
}
root=_Merge(_Merge(x,_New(ai*(sz[x]+1))),y);
}
void Calc(){
cs=0;
_Calc(root);
}
}mt;
signed main(){
n=read();
forup(i,1,n){
a[i]=read();
}
forup(i,1,n){
mt.Insert(a[i]);
}
mt.Calc();
i64 ans=0,sum=0;
forup(i,1,n){
sum+=seq[i];
ans=max(ans,sum);
}
printf("%lld\n",ans);
}
P7811 [JRKSJ R2] 你的名字。
建议改为:【模板】比较毒瘤的根号分治(话说根号分治/根号均摊毕竟是一种思维方式,不太好找模板)
我不太喜欢这种码量远大于思维量的题,但在学校这样的题真的是消磨时间的好方法。
可以说是本套题里面最毒瘤的了。
看到取模运算应该先想到根号分治(当然有些时候应该想到势能分析,取决于有没有区间修改之类的操作)。
首先设一个阈值 $T$。
对于 $k\le T$,这样的 $k$ 最多有 $T$ 个,那么我们可以把询问离线挂到 $k$ 上,对于每个 $k$ 预处理 $a_i\bmod k$ 的区间最大值,线段树建树是 $O(n)$ 的,然后查询复杂度和询问次数有关,我们暂且记单次查询是 $O(\log n)$ 的,等会跟后面的操作取 $\max$,这部分总复杂度 $O(Tn)$。
对于 $k>T$,这部分就难搞了。
首先这样的 $k$ 的倍数个数肯定 $\le \frac{n}{T}$ 吧。
那么我们大体思路就是维护大于每个倍数 $p$ 的区间最小值。
具体一点,给序列里的数 $a$ 和所有倍数 $p$ 放到一起排序,从大到小扫一遍,每次遇到 $a$ 就插入一个支持区间查最小值的数据结构里,遇到 $p$ 就查询。
那么我们先考虑数据结构的选择,查询次数的上界是 $q\frac{V}{T}$,那我们查询只能是 $O(1)$ 的。考虑猫树或者 ST 表。但是我不会猫树,直接考虑 ST 表。
但是这里又有个问题,ST 不能快速地插入新数据,复杂度最优是 $O(n)$ 的($2^0+2^1+\dots +2^{\log n}=n$)。那么我们又考虑根号均摊,先分块,求出每一块的最小值,然后对块建立 ST 表,设块长为 $P$,这样复杂度就降到 $O(\frac{n}{P}+P)$ 的了,然后对于散块我们可以 $O(P)$ 预处理前后缀最小值,这样查询就是 $O(1)$ 的了,对于每个询问就是 $O(\frac{V}{T})$ 的。
这又涉及到一个问题,假如某区间左右端点都在同一块里应该怎么做。这个操作需要我们跳出思维的陷阱,既然都在同一块里了那直接暴力复杂度就是 $O(L)$ 的,完全可以通过,我们把在同一块里的额外分开算即可。
OK 刨开这个问题,我们又有另一个问题,这道题卡空间。
刚刚我们构想的算法空间复杂度是 $O(q\frac{V}{T})$ 的,这道题空间限制是 128MB,进行一些简单的计算容易发现最多开 $128\times 1024\times 1024\times \frac{1}{4}=33554432$ 个 int 型变量。如果要保证空间 $T$ 至少要开到 $\frac{q\times V}{33554432}\approx 900$,而且再算上栈空间之类的 $T$ 至少要开到 $2000$,那么前面 $O(Tn)$ 的时间复杂度就超了。
所以我们不能试图通过调整块长的方法解决空间问题。
那么考虑换一种思路。我们一眼就看到这道题值域比较小,那么我们把 $a$ 挂在值域上然后从大到小枚举每个数,对于每个数可以 $O(\sqrt{V})$ 地枚举因子判断有没有询问挂在这个数上,这样时间复杂度就在外部加上了一个 $O(V\sqrt{V})$,但是空间复杂度变成 $O(n+q)$ 的了,可以接受。
然后注意一下,$0$ 是任何数的倍数,要特别处理一下。
综合来说,我们分成三部分考虑:
- $r-l+1\le L$,直接暴力。
- $k\le T$,见上文第一类
- $k> T$ 见上文第二类。
然后分析一下块长,这样做下来复杂度是 $O(V\sqrt{V}+q\max(\frac{V}{T},P)+\frac{n^2}{P}+nP+Tn)$ 的。
由于不带 $\log$,我们考虑 $P$ 取 $\sqrt{n}$,$T$ 取 $\sqrt{V}$,那么复杂度就是 $O((n+V)\sqrt{V}+(n+q)\sqrt{n})$ 的了,差不多是 $O(n\sqrt{n})$ 级别的(大道至简了属于是)。
思维难度不算太高,但代码难度比较高。
参考代码 updated on 25 Sept.
其实写起来也没想象的那么难,就是卡常有点折磨。
附带卡常的技巧:
- 假如同时满足第一个和第二个条件,可以判断一下用哪个方法更快($r-l$ 较小就用第一个)。
- 第二种可以用 Barrett 取模优化,因为同一个模数会用 $n$ 次,确实会快一点。
- ST 表把指数那一维放到第一维,这样内存更连续一些。
- C++20 好像对函数和结构体有优化,建议使用 C++20
- 有些只用一次的数据结构可以不用结构体封装,封装会变慢的(虽然我代码里只有 ST 表没封装)。
- 根据不同操作的常数微调块长(说是微调,但是我最终过的那个代码已经把应该等于 $\sqrt{V}$ 的 $T$ 调的比应该等于 $\sqrt{n}$ 的 $P$ 还大了)。
- 剪枝(已经是老生常谈了吧)
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);++i)
#define fordown(i,s,e) for(int i=(s);i>=(e);--i)
using namespace std;
char buf[1<<15],*p1=buf,*p2=buf;
#define gc (p1==p2&&(p2=buf+fread(p1=buf,1,1<<15,stdin),p1==p2)?-1:*p1++)
inline int read()
{
int x=0;char c=gc;
for(;!isdigit(c);c=gc);
for(; isdigit(c);c=gc) x=(x<<3)+(x<<1)+(c^48);
return x;
}
#define ull unsigned long long
#define ui128 __uint128_t
struct Barrett{
ull d;ui128 m;
void init(ull _d){
d=_d,m=(((ui128)(1)<<64)/d);
}
ull operator()(ull a){
ull w=(m*a)>>64;w=a-w*d;
if(w>=d)w-=d;return w;
}
}MOD;
const int N=3e5,NN=1<<19,M=1e5,P=590,T=600,inf=0x3f3f3f3f;
int n,m,a[N+5],ans[N+5],blg[N+5],L[P+5],R[P+5],cp,mxa=0;
struct SegTree{
int querymin[NN<<1];
void Build(){
forup(i,1,n){
querymin[NN+i]=MOD(a[i]);
}
fordown(i,NN,1){
querymin[i]=min(querymin[i<<1],querymin[i<<1|1]);
}
}
int AskMin(int l,int r){
int res=inf;
for(l+=NN-1,r+=NN+1;l^r^1;l>>=1,r>>=1){
if(!(l&1)) res=min(res,querymin[l^1]);
if( r&1 ) res=min(res,querymin[r^1]);
}
return res;
}
}mt;
struct Node{
int l,r,pos;
};
vector<Node> qa[T+5],qb[M+5];
vector<int> na[M+5];
int lg[P+5];
int g[11][P+5];
void init(){
mem(g,0x3f);
}
void Update(int p,int x){
g[0][p]=x;
forup(i,1,10){
int q=max(p-(1<<i)+1,1);
fordown(j,p,q){
g[i][j]=min(g[i-1][j],g[i-1][j+(1<<(i-1))]);
}
}
}
int query(int l,int r){
int len=lg[r-l+1];
return min(g[len][l],g[len][r-(1<<len)+1]);
}
int mn[P+5],pre[P+5][P+5],suf[P+5][P+5];
int calc(int l,int r){
int tl=blg[l],tr=blg[r],res=inf;
res=min(suf[tl][l-L[tl]+1],pre[tr][r-L[tr]+1]);
if(tr>tl+1) res=min(res,query(tl+1,tr-1));
return res;
}
signed main(){
n=read();m=read();
forup(i,1,n){
a[i]=read();
na[a[i]].push_back(i);
mxa=max(mxa,a[i]);
}
lg[1]=0;
forup(i,2,P){
lg[i]=lg[i>>1]+1;
}
cp=n/P;
forup(i,1,cp){
L[i]=R[i-1]+1;R[i]=P*i;
forup(j,L[i],R[i]) blg[j]=i;
}
if(R[cp]!=n){
++cp;
L[cp]=R[cp-1]+1;R[cp]=n;
forup(i,L[cp],R[cp]) blg[i]=cp;
}
mem(ans,0x3f);
MOD.init(mxa+1);
mt.Build();
forup(Case,1,m){
int l=read(),r=read(),k=read();
if(k<=T){
if(blg[l]==blg[r]&&r-l<19){
forup(i,l,r){
ans[Case]=min(ans[Case],a[i]%k);
}
}else{
qa[k].push_back(Node{l,r,Case});
}
}else if(blg[l]==blg[r]){
forup(i,l,r){
ans[Case]=min(ans[Case],a[i]%k);
}
}else{
qb[k].push_back(Node{l,r,Case});
ans[Case]=mt.AskMin(l,r);
}
}
forup(i,1,T){
if(qa[i].empty()) continue;
MOD.init(i);
mt.Build();
for(auto j:qa[i]){
ans[j.pos]=mt.AskMin(j.l,j.r);
}
}
init();
mem(mn,0x3f);mem(suf,0x3f);mem(pre,0x3f);
fordown(i,mxa,T+1){
for(auto j:na[i]){
int tt=blg[j];
if(mn[tt]>i){
mn[tt]=i;
Update(tt,i);
}
forup(k,j,R[tt]){
pre[tt][k-L[tt]+1]=i;
}
fordown(k,j,L[tt]){
suf[tt][k-L[tt]+1]=i;
}
}
for(int j=1;j*j<=i;++j){
if(!(i%j)){
for(auto k:qb[j]){
ans[k.pos]=min(ans[k.pos],calc(k.l,k.r)-i);
}
for(auto k:qb[i/j]){
ans[k.pos]=min(ans[k.pos],calc(k.l,k.r)-i);
}
}
}
}
forup(i,1,m){
printf("%d\n",ans[i]);
}
}
CF1368H2 Breadboard Capacity (hard version)
看到这道题很像网络流中的最大流模型,但是数据范围很大,网络流会 T,那么考虑模拟网络流。
我们先把模建出来。
首先把每个端口视为一个点,红点连源点,蓝点连汇点。然后矩阵内每个点和四连通的四个点连边,所有边容量均为 $1$。这个比较显然,一个流就是一根导线。
然后根据最大流最小割定理,考虑求最小割。
最小割是把图上的点分为两个集合,那么考虑把矩阵内的点涂成红色和蓝色,表示处于源点/汇点所在的集合(和端口一致),那么若一条边两端颜色不同,它就会给割产生一个贡献(如果是最小割那么必然每条割边都是满流的,不然它就不是一个最小割)。
但是这样仍然不好维护,如果考虑轮廓线 DP 复杂度会飙到指数级别,而且也没什么很好的其它方法。考虑寻找性质。
容易发现,假如有一个这样的图形:
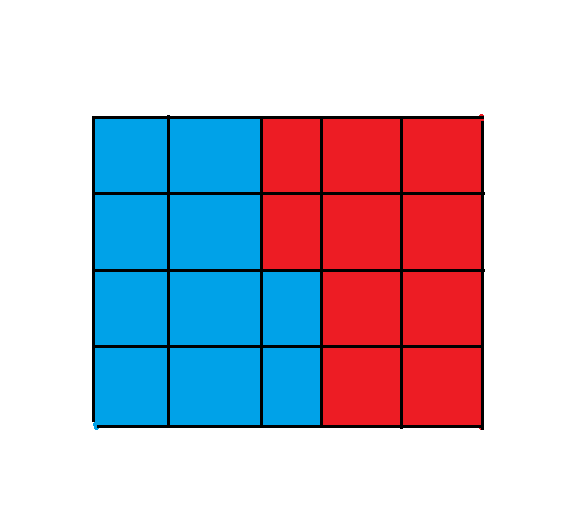
画的不太好,将就一下。
由于那么把第二行第三列的红点旁边有两个蓝点,那么把它涂成蓝色是必定不劣的(贡献 $-2+2$)。也就是说,必定能构造出最优情况,使得每个点附近至多有一个点与它颜色不同。
这意味着什么?意味着(不看边缘的端口)必定是一整行一整行全是同一种颜色(或者一整列一整列)!
由于行和列是对称的,我们单独考虑列。
那么可以设 $dp_{i,0/1}$ 表示考虑前 $i$ 列,第 $i$ 列是红色/蓝色的最小割,转移是简单的,枚举上一个颜色即可(我觉得都不太能算枚举了,就两种情况,可以算分讨了)。
$$ dp_{i,0}=\min(dp_{i-1,0},dp_{i-1,1}+n)+c_{i,1}\\ dp_{i,1}=\min(dp_{i-1,1},dp_{i-1,0}+n)+c_{i,0} $$
其中 $c_{i,0/1}$ 表示第 $i$ 列上下两端口中红色/蓝色端口的个数,$n$ 为行数。
然后注意初值考虑左边缘,答案考虑右边缘。
显然,第一维可以滚动掉,对横竖各求一遍 DP 就可以过 easy version 啦 ✿✿ヽ(°▽°)ノ✿。
hard version 变成动态的了,那么考虑动态 DP,此处仍只考虑列,行是对称的。
此处定义 $2\times 2$ 矩阵的广义矩阵乘法 $A\otimes B=C$:
$$C_{i,j}=\min_{k=0}^{1}\begin{Bmatrix}A_{i,k}+B_{k,j}\end{Bmatrix}$$
不看第一维,我们的状态就是:
$$\begin{bmatrix}dp_0&dp_1\end{bmatrix}$$
首先考虑转移中的矩阵,设转移的矩阵为 $A_i$,那么我们希望它满足如下式子:
$$\begin{bmatrix}dp_0&dp_1\end{bmatrix}\otimes A_i=\begin{bmatrix}\min(dp_{i-1,0},dp_{i-1,1}+n)+c_{i,1}&min(dp_{i-1,1},dp_{i-1,0}+n)+c_{i,0}\end{bmatrix}$$
由于后面的那个加数不太好维护,我们把它塞到 $\min$ 里面:
$$\begin{bmatrix}dp_0&dp_1\end{bmatrix}\otimes A_i=\begin{bmatrix}\min(dp_{i-1,0}+c_{i,1},dp_{i-1,1}+n+c_{i,1})&\min(dp_{i-1,1}+c_{i,0},dp_{i-1,0}+n+c_{i,0})\end{bmatrix}$$
自己手玩一下,可以得到 $A_i$:
$$A_i=\begin{bmatrix}c_{i,1} &c_{i,0}+n\\ c_{i,1}+n &c_{i,0}\end{bmatrix}$$
然后初末状态就是左/右边缘的红蓝点数,具体怎么样塞到矩阵(向量?)里就略过了。
然后考虑如何维护反转操作,其实也很简单,对每一列维护四个矩阵,分别代表上下均不反转,上边缘反转,下边缘反转,上下均反转,在线段树维护的时候同时合并这四个信息即可。初末状态可以单独取出来放在线段树外面用另一棵线段树维护。
然后和 easy version 一样,对横竖各维护一边就可以啦 ✿✿ヽ(°▽°)ノ✿。
复杂度 $O(q\log n)$,带 $2^3$ 倍常数。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
//#define DEBUG
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=1e5+5,inf=0x3f3f3f3f;
struct Matrix{
int c[2][2];
Matrix(int _=inf,int __=inf,int ___=inf,int ____=inf){
c[0][0]=_;
c[0][1]=__;
c[1][0]=___;
c[1][1]=____;
}
Matrix operator *(const Matrix &r){
Matrix res(inf,inf,inf,inf);
forup(i,0,1){
forup(j,0,1){
forup(k,0,1){
res.c[i][j]=min(res.c[i][j],c[i][k]+r.c[k][j]);
}
}
}
return res;
}
};
struct SegTree1{
#define mid ((l+r)>>1)
#define lson l,mid,id<<1
#define rson mid+1,r,id<<1|1
private:
Matrix querymul[4][N<<2];
int mark[N<<2],mm;
void PushUp(int id){
forup(i,0,3){
querymul[i][id]=querymul[i][id<<1]*querymul[i][id<<1|1];
}
}
void Revup(int id){
swap(querymul[0][id],querymul[2][id]);
swap(querymul[1][id],querymul[3][id]);
mark[id]^=2;
}
void Revdown(int id){
swap(querymul[0][id],querymul[1][id]);
swap(querymul[2][id],querymul[3][id]);
mark[id]^=1;
}
void PushDown(int id){
if(mark[id]&1){
Revdown(id<<1);Revdown(id<<1|1);
}
if(mark[id]&2){
Revup(id<<1);Revup(id<<1|1);
}
mark[id]=0;
}
public:
void Build(int A[2][N],int l,int r,int id){
if(l==r){
querymul[0][id]=Matrix( A[1][l]+A[0][l] , 2-(A[1][l]+A[0][l])+mm, A[1][l]+A[0][l]+mm , 2-(A[1][l]+A[0][l]) );
querymul[1][id]=Matrix( A[1][l]+(1-A[0][l]), (1-A[1][l])+A[0][l]+mm, A[1][l]+(1-A[0][l])+mm, (1-A[1][l])+A[0][l] );
querymul[2][id]=Matrix( (1-A[1][l])+A[0][l], A[1][l]+(1-A[0][l])+mm, (1-A[1][l])+A[0][l]+mm, A[1][l]+(1-A[0][l]) );
querymul[3][id]=Matrix( 2-(A[1][l]+A[0][l]), A[1][l]+A[0][l]+mm , 2-(A[1][l]+A[0][l])+mm, A[1][l]+A[0][l] );
return;
}
Build(A,lson);Build(A,rson);
PushUp(id);
}
void init(int _mm){
mm=_mm;
}
void Modify(int L,int R,int P,int l,int r,int id){
if(L<=l&&r<=R){
if(P==2) Revup(id);
else Revdown(id);
return;
}
if(mark[id]) PushDown(id);
if(L<=mid) Modify(L,R,P,lson);
if(mid< R) Modify(L,R,P,rson);
PushUp(id);
}
Matrix Ask(){
return querymul[0][1];
}
};
struct SegTree2{
private:
int querysum[N<<2],mark[N<<2];
void PushUp(int id){
querysum[id]=querysum[id<<1]+querysum[id<<1|1];
}
void PushDown(int id,int len){
querysum[id<<1]=(len-(len>>1))-querysum[id<<1];
querysum[id<<1|1]=(len>>1)-querysum[id<<1|1];
mark[id<<1|1]^=1;
mark[id<<1]^=1;
mark[id]=0;
}
public:
void Build(int A[N],int l,int r,int id){
if(l==r){
querysum[id]=A[l];
return;
}
Build(A,lson);Build(A,rson);
PushUp(id);
}
void Modify(int L,int R,int l,int r,int id){
if(L<=l&&r<=R){
querysum[id]=r-l+1-querysum[id];
mark[id]^=1;
return;
}
if(mark[id]) PushDown(id,r-l+1);
if(L<=mid) Modify(L,R,lson);
if(mid< R) Modify(L,R,rson);
PushUp(id);
}
int Ask(){
return querysum[1];
}
};
SegTree1 th,ts;
SegTree2 th0,th1,ts0,ts1;
int n,m,q;
int ch[2][N],cs[2][N];
char str[N];
int calc(){
int rh0=th0.Ask(),rh1=th1.Ask();
int rs0=ts0.Ask(),rs1=ts1.Ask();
int res=inf;
Matrix mm=Matrix(rh0,m-rh0,inf,inf)*ts.Ask()*Matrix(rh1,inf,m-rh1,inf);
#ifdef DEBUG
printf("%d %d %d %d\n",rh0,rh1,rs0,rs1);
forup(i,0,1){
forup(j,0,1){
printf("%d ",mm.c[i][j]);
}
puts("");
}
#endif
res=min(res,mm.c[0][0]);
mm=Matrix(rs0,n-rs0,inf,inf)*th.Ask()*Matrix(rs1,inf,n-rs1,inf);
#ifdef DEBUG
forup(i,0,1){
forup(j,0,1){
printf("%d ",mm.c[i][j]);
}
puts("");
}
#endif
res=min(res,mm.c[0][0]);
return res;
}
signed main(){
n=read();m=read();q=read();
th.init(n);ts.init(m);
scanf(" %s",str+1);
forup(i,1,n) cs[0][i]=(str[i]=='B');
scanf(" %s",str+1);
forup(i,1,n) cs[1][i]=(str[i]=='B');
scanf(" %s",str+1);
forup(i,1,m) ch[0][i]=(str[i]=='B');
scanf(" %s",str+1);
forup(i,1,m) ch[1][i]=(str[i]=='B');
th.Build(ch,1,m,1);ts.Build(cs,1,n,1);
ts0.Build(cs[0],1,n,1);ts1.Build(cs[1],1,n,1);
th0.Build(ch[0],1,m,1);th1.Build(ch[1],1,m,1);
printf("%d\n",calc());
forup(Case,1,q){
char op;
scanf(" %1c",&op);
int l=read(),r=read();
if(op=='L'){
ts0.Modify(l,r,1,n,1);
ts.Modify(l,r,1,1,n,1);
}else if(op=='R'){
ts1.Modify(l,r,1,n,1);
ts.Modify(l,r,2,1,n,1);
}else if(op=='U'){
th0.Modify(l,r,1,m,1);
th.Modify(l,r,1,1,m,1);
}else{
th1.Modify(l,r,1,m,1);
th.Modify(l,r,2,1,m,1);
}
printf("%d\n",calc());
}
}