2023 南京集训 杂题
Day 3 模拟赛 T3
考虑一个贪心,先把所有人放在一队,每次从两队中随便选一个不合法的放到另一队,直到选不出为止。
这个贪心为什么是对的?
首先边数是 $O(n)$ 级别的(大前提)。
然后假如一个点不合法说明它连了至少两条边,放到另一队里至多增加一条边,会使得总边数至少减一。
最终一定会减到合法为止,且最多需要减 $O(n)$ 次。假如暴力找不合法的就是 $O(n^2)$,可以通过。
据说还有神秘做法可以 $O(1)$ 查找不合法,复杂度就是线性的,但我不会,讲题的也没讲。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=7005,inf=0x3f3f3f3f;
int n,c[N],d[N],sd[N];
vector<int> e[N];
bool work(){
forup(i,1,n){
if(d[i]>1){
for(auto j:e[i]){
if(sd[j]==sd[i]) d[j]--;
else d[j]++;
}
d[i]=c[i]-d[i];
sd[i]^=1;
return true;
}
}
return false;
}
void print(){
int c1=0,c0=0;
forup(i,1,n){
if(sd[i]==1) c1++;
else c0++;
}
if(c1<c0){
printf("%d\n",c1);
forup(i,1,n){
if(sd[i]==1) printf("%d ",i);
}
}else if(c1>c0){
printf("%d\n",c0);
forup(i,1,n){
if(sd[i]==0) printf("%d ",i);
}
}else{
printf("%d\n",c1);
forup(i,1,n){
if(sd[i]==sd[1]) printf("%d ",i);
}
}
}
signed main(){
n=read();
forup(i,1,n){
d[i]=c[i]=read();
sd[i]=0;
forup(j,1,c[i]){
int v=read();
e[i].push_back(v);
}
}
while(work());
print();
}
Day 3 模拟赛 T4
发现正着做不太好做,考虑反着求不满足 $a \to b \to c \to a$ 的三元组个数。
由于是个比赛图,所以不满足的三元组必定是 $a \to b,a \to c,b\to c/c \to b$。
换句话说,在一个点指向的点中随便选两个都不合法。
然后就很简单了,线段树维护每个点在修改后的出边个数。具体来说,假如不修改,那么出边个数就是比它小的数的个数。然后开一棵线段树维护区间异或 $1$,区间求和即可。结合双指针复杂度 $O(n\log n+m)$。
然后组合数求解即可。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(i64 i=(s);i<=(e);i++)
#define fordown(i,s,e) for(i64 i=(s);i>=(e);i--)
using namespace std;
using i64=long long;
#define gc getchar()
inline i64 read(){
i64 x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const i64 N=1e5+5,inf=0x3f3f3f3f;
i64 n,m,a[N];
struct op{
i64 l,r;
}q1[N],q2[N];
struct SegmentTree{
#define mid ((l+r)>>1)
#define lson l,mid,id<<1
#define rson mid+1,r,id<<1|1
i64 querysum[N<<2],mark[N<<2];
void PushUp(i64 id){
querysum[id]=querysum[id<<1]+querysum[id<<1|1];
}
void PushDown(i64 id,i64 len){
mark[id]=0;
mark[id<<1]^=1;mark[id<<1|1]^=1;
querysum[id<<1|1]=(len>>1)-querysum[id<<1|1];
querysum[id<<1]=(len-(len>>1))-querysum[id<<1];
}
void Modify(i64 L,i64 R,i64 l=1,i64 r=n,i64 id=1){
if(R<L) return;
if(L<=l&&r<=R){
mark[id]^=1;
querysum[id]=(r-l+1)-querysum[id];
return;
}
if(mark[id]) PushDown(id,r-l+1);
if(L<=mid) Modify(L,R,lson);
if(mid< R) Modify(L,R,rson);
PushUp(id);
}
i64 AskSum(i64 L,i64 R,i64 l=1,i64 r=n,i64 id=1){
if(R<L) return 0;
if(L<=l&&r<=R){
return querysum[id];
}
if(mark[id]) PushDown(id,r-l+1);
i64 res=0;
if(L<=mid) res+=AskSum(L,R,lson);
if(mid< R) res+=AskSum(L,R,rson);
return res;
}
}mt;
bool cmp1(op a,op b){
if(a.l!=b.l) return a.l<b.l;
return a.r<b.r;
}
bool cmp2(op a,op b){
if(a.r!=b.r) return a.r<b.r;
return a.l<b.l;
}
i64 ans;
signed main(){
n=read();m=read();
ans=n*(n-1)*(n-2)/6;
forup(i,1,n){
a[i]=read();
}
sort(a+1,a+n+1);
forup(i,1,m){
int l=read(),r=read();
q1[i].l=q2[i].l=lower_bound(a+1,a+n+1,l)-a;
q1[i].r=q2[i].r=upper_bound(a+1,a+n+1,r)-a-1;
}
sort(q1+1,q1+m+1,cmp1);
sort(q2+1,q2+m+1,cmp2);
mt.Modify(1,n);
i64 p1=1,p2=1;
forup(i,1,n){
mt.Modify(i,i);
while(p1<=m&&q1[p1].l<=i){
mt.Modify(q1[p1].l,q1[p1].r);
++p1;
}
while(p2<=m&&q2[p2].r<i){
mt.Modify(q2[p2].l,q2[p2].r);
++p2;
}
i64 res=mt.AskSum(1,i-1)+mt.AskSum(i+1,n);
ans-=res*(res-1)/2;
}
printf("%lld",ans);
}
[AGC030D] Inversion Sum
直接做完全没思路。这种情况有个套路,就是转化成期望 DP 再最终乘以某个数,利用期望的线性性求解。
设 $dp_{p,i,j}$ 表示考虑前 $p$ 个操作,假设每个操作有 $\frac{1}{2}$ 的概率不进行,$a_i>a_j$ 的概率是多少。转移是简单的,先计算 $dp_{p,x_p,y_p}$ 和 $$dp_{p,y_p,x_p},然后直接枚举除去这一步交换的两个位置以外的其它位置,由于这一步只有 $x_p,y_p$ 可能变化,所以只有 $O(n)$ 的状态会变化。最终统计 $i>j,a_i<a_j$ 的二元组 $(i,j)$ 个数,乘以 $2^Q$ 即可。
然后可以把 $p$ 这一维压掉。
这道题主要难在不知道套路一点思路都想不出来。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=3005,inf=0x3f3f3f3f,mod=1e9+7;
int n,a[N],m,x,y,dp[N][N],pw=1;
int inv2=(mod+1)/2;
signed main(){
n=read();m=read();
forup(i,1,n){
a[i]=read();
}
forup(i,1,n){
forup(j,1,n){
dp[i][j]=(a[i]>a[j]);
}
}
forup(i,1,m){
(pw*=2)%=mod;
x=read();y=read();
dp[x][y]=dp[y][x]=1ll*(dp[x][y]+dp[y][x])*inv2%mod;
forup(j,1,n){
if(j==x||j==y) continue;
dp[x][j]=dp[y][j]=1ll*(dp[x][j]+dp[y][j])*inv2%mod;
dp[j][x]=dp[j][y]=1ll*(dp[j][x]+dp[j][y])*inv2%mod;
}
}
int ans=0;
forup(i,1,n){
forup(j,i+1,n){
(ans+=dp[i][j])%=mod;
}
}
printf("%lld\n",1ll*ans*pw%mod);
}
P9197 [JOI Open 2016] 摩天大楼
很有意思的一道题,第一步的转化很巧妙。
首先从 $f$ 的顺序角度考虑显然是不可做的,考虑把所有数拍在一个二维平面上。
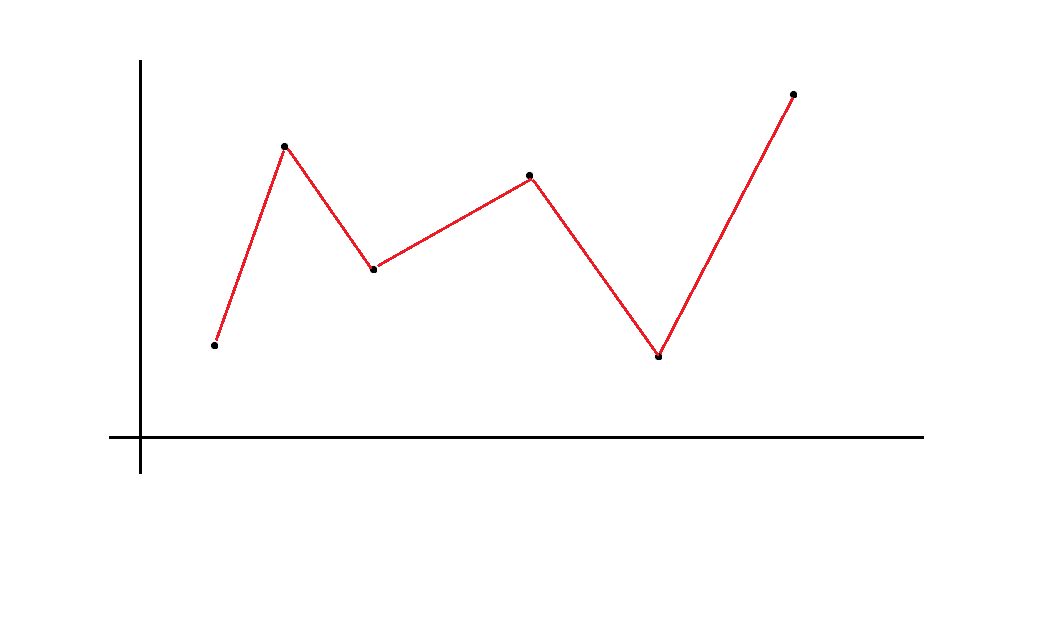
那么其实就是要求折线总纵向长度。
那么考虑从上到下用一个类似扫描线的东西。发现只要知道之前有几段连续的,下一层的贡献其实是唯一确定的。
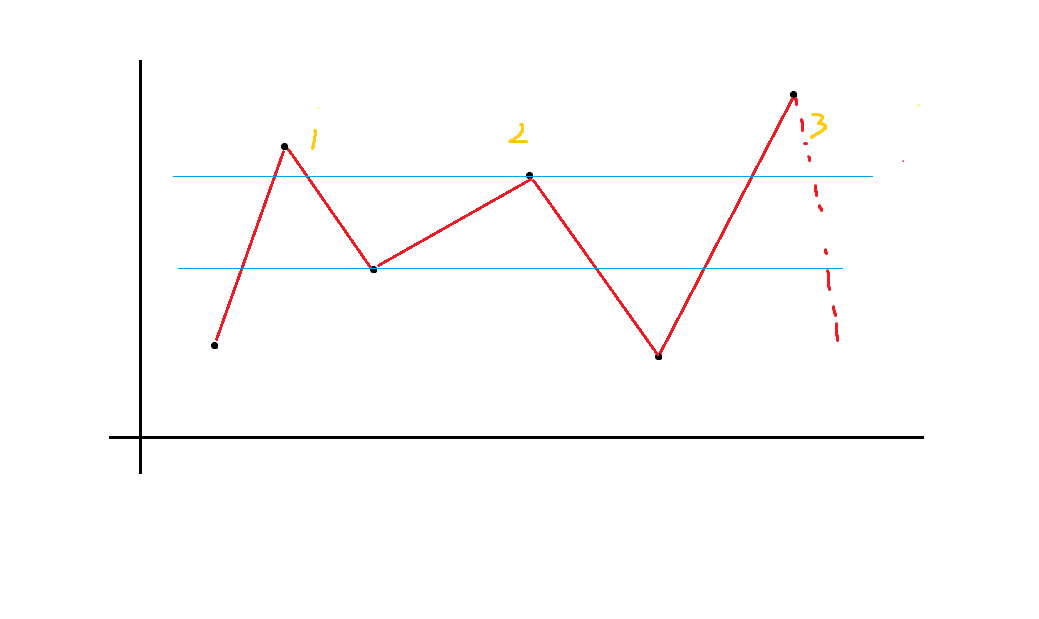
上图中这一层有 $5\times (f_4-f_3)$ 的贡献,因为右侧已经到头了。
那么考虑排降序后 DP,设 $dp_{i,j,k,0/1,0/1}$ 表示放入(排序后)前 $i$ 个,分了 $j$ 个连续段,总和为 $k$,左/右有没有抵到边界的方案数。转移就分三种情况考虑:
- 新开一段。
- 并入之前的某一段。
- 合并原先的两段。
具体方程略。最后答案就是 $\sum_{i=0}^kdp_{n,1,i,1,1}$。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=105,M=1005,inf=0x3f3f3f3f,mod=1e9+7;
int n,m,a[N],dp[2][N][M][2][2],ans=0;
signed main(){
n=read();m=read();
forup(i,1,n){
a[i]=read();
}
sort(a+1,a+n+1,greater<int>());
dp[1][1][0][0][0]=dp[1][1][0][0][1]=dp[1][1][0][1][0]=dp[1][1][0][1][1]=1;
forup(i,2,n){
int o=i&1,r=o^1;
mem(dp[o],0);
forup(j,1,i-1){
forup(k,0,m){
forup(p,0,1){
forup(q,0,1){
if(!dp[r][j][k][p][q]) continue;
int nxt=k+(2*j-p-q)*(a[i-1]-a[i]);
if(nxt>m) continue;
if(j>1){
(dp[o][j+1][nxt][p][q]+=1ll*(j-1)*dp[r][j][k][p][q]%mod)%=mod;
(dp[o][j][nxt][p][q]+=2ll*(j-1)*dp[r][j][k][p][q]%mod)%=mod;
(dp[o][j-1][nxt][p][q]+=1ll*(j-1)*dp[r][j][k][p][q]%mod)%=mod;
}
if(!p){
(dp[o][j+1][nxt][0][q]+=dp[r][j][k][p][q])%=mod;
(dp[o][j+1][nxt][1][q]+=dp[r][j][k][p][q])%=mod;
(dp[o][j][nxt][0][q]+=dp[r][j][k][p][q]%mod)%=mod;
(dp[o][j][nxt][1][q]+=dp[r][j][k][p][q]%mod)%=mod;
}
if(!q){
(dp[o][j+1][nxt][p][0]+=dp[r][j][k][p][q])%=mod;
(dp[o][j+1][nxt][p][1]+=dp[r][j][k][p][q])%=mod;
(dp[o][j][nxt][p][0]+=dp[r][j][k][p][q]%mod)%=mod;
(dp[o][j][nxt][p][1]+=dp[r][j][k][p][q]%mod)%=mod;
}
}
}
}
}
}
int ans=0;
forup(i,0,m){
(ans+=dp[n&1][1][i][1][1])%=mod;
}
printf("%d",ans);
}
[AGC033D] Complexity
貌似是很经典的一道套路题。
首先 $O(n^5)$ 的记忆化搜索很简单,不多讲了。设状态 $f_{x_1,y_1,x_2,y_2}$ 表示左上角为 $(x_1,y_1)$,右下角为 $(x_2,y_2)$ 的矩形的复杂度。这种情况状态是 $O(n^4)$ 级别的,考虑先想办法压一维状态,然后把转移控制在大约 $\log$ 的复杂度内。
首先考虑最坏情况,即要把整个矩阵剁成一格一格的臊子。发现此时答案为 $\left\lceil\log n\right\rceil+\left\lceil\log m\right\rceil\le 20$。
那么发现答案的级别很小,考虑把答案和状态的某一维交换。
具体来说,设 $f_{x_1,x_2,y,c}$ 表示矩阵左边为一条从 $(x_1,y)$ 到 $(x_2,y)$ 的线段,复杂度为 $c$ 的矩阵右边缘最多延伸到多远(我定义的是左闭右闭区间,貌似左闭右开会好写一点)。
那么转移分两种,横着切的转移和竖着切的转移。
首先是竖着切的转移,由于切一刀只会增加 $1$ 复杂度,所以转移和倍增类似,即:
$$dp_{x_1,x_2,y,c}=dp_{x_1,x_2,dp_{x_1,x_2,y,c-1}+1,c-1}$$
然后考虑横着切的转移,发现其实就是要求这个式子(类似于区间 DP):
$$dp_{x_1,x_2,y,c}=\max_{mid=x_1}^{x_2}\begin{Bmatrix}\min(dp_{x_1,mid,y,c-1},dp_{mid+1,x_2,y,c-1})\end{Bmatrix}$$
容易发现 $dp_{x_1,mid,y,c-1}$ 随着 $mid$ 的增加单调不增,$dp_{mid+1,x_2,y,c-1}$ 随着 $mid$ 增加单调不减,那么在它们取等的时候显然 $\min(dp_{x_1,mid,y,c-1},dp_{mid+1,x_2,y,c-1})$ 取到最大值,我们可以二分这个点。
复杂度 $O(n^2m(\log n+\log m)\log n)$ 带小常数,随便过。
/// details | 参考代码 oprn: False type: success
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=200,inf=0x3f3f3f3f;
int n,m,a[N][N],sum[N][N],dp[25][N][N][N];
char str[N];
int calc(int x1,int x2,int y1,int y2){
return sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1];
}
signed main(){
n=read();m=read();
forup(i,1,n){
scanf(" %s",str+1);
forup(j,1,m){
a[i][j]=(str[j]=='#');
sum[i][j]=a[i][j]+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
}
}
forup(x1,1,n){
forup(x2,x1,n){
forup(y,1,m){
if(calc(x1,x2,y,y)!=0&&calc(x1,x2,y,y)!=(x2-x1+1)){
continue;
}
int ll=y,rr=m,mid;
while(ll<rr){
mid=(ll+rr+1)>>1;
if(calc(x1,x2,y,mid)==0||calc(x1,x2,y,mid)==(x2-x1+1)*(mid-y+1)) ll=mid;
else rr=mid-1;
}
dp[0][x1][x2][y]=ll;
}
}
}
forup(i,1,20){
forup(len,1,n){
forup(x1,1,n-len+1){
int x2=x1+len-1;
fordown(y,m,1){
if(dp[i][x1][x2][y]) continue;
if(dp[i-1][x1][x2][y]==m){
dp[i][x1][x2][y]=m;
continue;
}
if(dp[i-1][x1][x2][y]!=0){
dp[i][x1][x2][y]=max(dp[i][x1][x2][y],dp[i-1][x1][x2][dp[i-1][x1][x2][y]+1]);
}
int ll=x1,rr=x2,mid;
while(ll<rr){
mid=(ll+rr)>>1;
if(dp[i-1][x1][mid][y]>=dp[i-1][mid+1][x2][y]) ll=mid+1;
else rr=mid;
}
dp[i][x1][x2][y]=max({dp[i][x1][x2][y],min(dp[i-1][x1][ll][y],dp[i-1][ll+1][x2][y]),min(dp[i-1][x1][ll-1][y],dp[i-1][ll][x2][y])});
}
}
}
}
forup(i,0,20){
if(dp[i][1][n][1]>=m){
printf("%d\n",i);
return 0;
}
}
}
///