扩展 KMP 算法(Z 函数)
今天刷题时看到了这么一个算法,主要是为了做题就学了一下。
概述
顾名思义,扩展 KMP 即 KMP 算法的扩展。但是总所周知 KMP 其实叫前缀函数,只是国内喜欢叫它 KMP 算法。同理,国外一般称扩展 KMP 算法为 Z Algorithm(Z 算法),但这都不太重要。
约定:字符串下标从 $0$ 开始
定义
对于一个长度为 $n$ 的字符串 $s$,定义函数 $z_i$ 表示 $s$ 和 $s$ 以 $i$ 开头的后缀的 LCP 的长度,其中 $z_i$ 被称为 Z 函数,特别地,$z_0=0$。
但是我不是这样理解的,为了实现方便,我定义了 $nxt_i$,大部分和 $z$ 相同,唯一不同在于 $nxt_0=n$。
求解
我曾经说过我对字符串算法的理解:
一堆看起来毫无卵用其实非常有用的东西。
所以我们先不讲用法,而是先讲求法。
首先有个显然的 $O(n^2)$ 暴力,在此不多赘述了。
观察模板题数据范围可知 扩展 KMP 有 $O(n)$ 的求法:
首先回顾一下我们是怎么求 KMP 的,先不管推出算法的思路是什么,最终算法就是利用先前求出的 $nxt_{0\le j< i}$ 求出 $nxt_i$。那么我们能否用类似的方法求出扩展 KMP 的 $nxt_i$ 呢?答案是肯定的。
首先,假设我们已经求出了 $0\le j<i$ 的 $nxt_j$,那么肯定存在一个 $0\le k<i$ 使得 $k+nxt_k-1$ 最大化,设这个最大的 $k+nxt_k-1=p$,这里暂且假定 $p\ge i$,我们画个图理解:
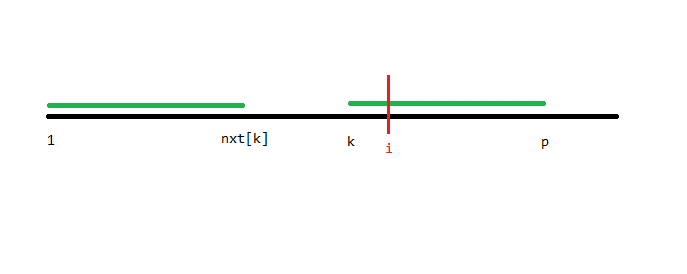
那么根据定义,上图中两段绿色线段是相等的。所以可以得出下图两段蓝色线段是相等的。
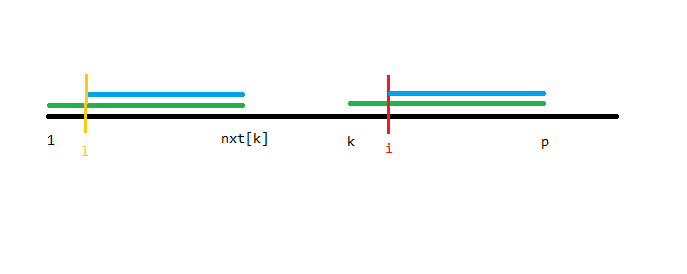
我们设 $l=i-k$,容易发现 $l$ 就是左边那段蓝色线段的开头。
那么容易想到 $nxt_l$ 可能有什么性质,我们分情况讨论一下。
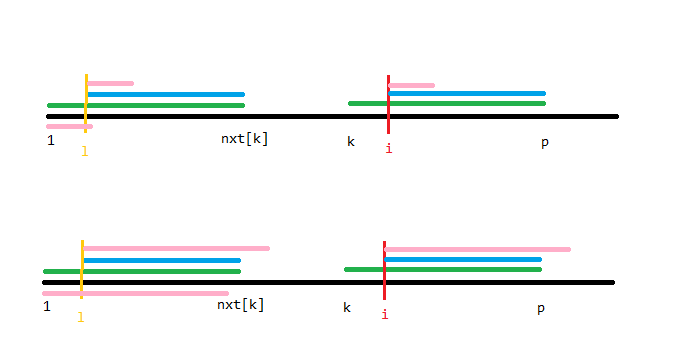
首先上面的情况,$nxt_l\le p-i$,这种情况下显然 $nxt_i=nxt_l$。
另一种情况,我们无法判断最后粉色线段冒出绿色线段的部分匹配的有多长,但无论如何 $i$ 都会成为新的 $k$(根据定义),那么 $p$ 只会单调向右移动,可以直接暴力移动 $p$ 求出 $nxt_i$。
然后我们就可以考虑 $p<i$ 的情况了,容易发现这直接可以相当于图 $3$ 下面的那种情况,就不多赘述了。
复杂度 $O(n)$。
参考代码
例题
字符串匹配
首先类似于普通的 KMP,exKMP 也可以做字符串匹配,具体来说,可以类似于 $nxt$ 的求法,求出模式串和文本串每个后缀的 LCP(类比普通 KMP),代码类似 $nxt$ 数组的求法。
参考代码
P7114 [NOIP2020] 字符串匹配
题意就是给你一个字符串,让你求出把字符串分为 $(AB)^iC$ 的方案数,其中 $A^i$ 表示把字符串 $A$ 循环 $i$ 遍,且要求 $A$ 中出现奇数次的字符个数小于 $C$。
先不考虑 $A$ 中出现奇数次的字符个数小于 $C$ 的条件,那么我们可以考虑枚举 $AB$ 及其循环次数。
这个问题就可以用 exKMP 解决(和 KMP 求出字符串最短循环节长度类似),先说结论,字符串 $s$ 中以长度为 $i$ 的前缀为循环节的前缀个数为:
$$\left\lfloor\frac{nxt_i}{i}\right\rfloor+1$$
证明:
考虑画图:
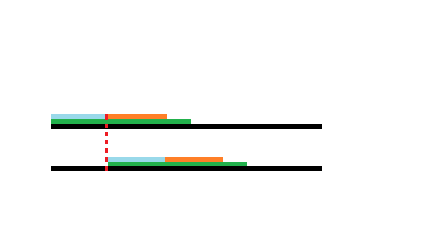
假如图中的绿色线段是一个 $nxt$,那么显然,两绿色段相等,因此两青色段相等,因此两橙色与青色段均相等,那么显然青色段就是一个循环节,而最多的循环次数为 $3$ 次,是 $\left\lfloor\frac{nxt_i}{i}\right\rfloor+1$。
然后考虑字符出现的次数,由于循环节是相等的,那么 $c$ 中字符出现次数的奇偶性只与 $AB$ 循环次数的奇偶性有关,用桶预处理一下每个前后缀奇数个数字符出现次数,分奇偶讨论后树状数组维护即可,具体方法参考原题题解。
参考代码
const i64 N=2e6+5,inf=0x3f3f3f3f;
i64 t,n,nxt[N],pre[N],suf[N],nw,ans;
char s[N];
void getnxt(){
i64 k=1,p=0;
while(p+1<n&&s[p]==s[p+1]) ++p;
nxt[1]=p;nxt[0]=n;
forup(i,2,n-1){
i64 p=k+nxt[k]-1,l=nxt[i-k];
if(i+l<=p){
nxt[i]=l;
}else{
i64 j=max(0ll,p-i+1);
while(i+j<n&&s[i+j]==s[j]) ++j;
nxt[i]=j;
k=i;
}
}
}
int bkt[26];
struct BIT{
int c[30];
void clear(){mem(c,0);}
void upd(int x,int k){++x;for(;x<=27;x+=x&-x)c[x]+=k;}
int sum(int x){++x;int res=0;for(;x>0;x-=x&-x)res+=c[x];return res;}
}mt;
signed main(){
t=read();
while(t--){
scanf(" %s",s);
n=strlen(s);
getnxt();
mem(bkt,0);
pre[0]=nw=1;bkt[s[0]-'a']=1;
forup(i,1,n-1){
nw-=bkt[s[i]-'a']%2;
bkt[s[i]-'a']++;
nw+=bkt[s[i]-'a']%2;
pre[i]=nw;
}
mem(bkt,0);
suf[n-1]=nw=1;bkt[s[n-1]-'a']=1;
fordown(i,n-2,0){
nw-=bkt[s[i]-'a']%2;
bkt[s[i]-'a']++;
nw+=bkt[s[i]-'a']%2;
suf[i]=nw;
}
mt.clear();
ans=0;
forup(i,2,n-1){
int p1=nxt[i]/i+1,t1=p1-p1/2,t2=p1/2;
mt.upd(pre[i-2],1);
if(p1*i==n){
if(p1&1) --t1;
else --t2;
}
ans+=mt.sum(suf[i])*t1;
ans+=mt.sum(suf[0])*t2;
}
printf("%lld\n",ans);
}
}