Manacher 算法
前言
我曾经说过一句话。
字符串算法就是一堆看起来没有卵用其实超级有用的东西。
但 Manacher 算法是少有的意义明确的字符串算法。
算法简述
Manacher 算法(国内俗称马拉车)由 Glenn K. Manacher 在 1975 年提出。是一种在能在线性时间内求出某字符串所有回文子串的算法,且相比其它复杂度相近算法压倒性地简单。
首先,给出问题的严谨描述:
给定一个长度为 $n$ 的字符串 $s$,请找到所有对 $(i, j)$ 使得子串 $s[i \dots j]$ 为一个回文串。当 $t = t_{\text{rev}}$ 时,字符串 $t$ 是一个回文串($t_{\text{rev}}$ 是 $t$ 的反转字符串)。
而回文串有一种更方便的表述方式,对于某个位置 $i$,我们令 $d_i$ 为以 $i$ 为对称轴的最长回文子串的长度。这样只能表示长度为奇数的回文子串,那么我们可以再令 $d_i'$ 为以 $i-1,i$ 间的间隔为对称轴的最长回文子串长度,这样就可以表示长度为偶数的回文子串了。
考虑如何暴力求解 $d$ 与 $d'$,其实很简单,枚举中心点暴力往两侧拓展即可,代码就不贴了。
然后考虑优化,这里只说如何求解 $d$,关于 $d'$ 的后面会详细说。
首先与 KMP 等字符串算法的思路类似,都考虑从之前的答案推出现在的答案。假如我们已经求出 $1\sim i-1$ 的答案,那么我们可以维护两个数 $l,r$ 表示右端点最大的回文子串的左右端点(当然你也可以维护能使得 $x+d_x$ 最大的 $x$),若当前 $i>r$,直接暴力拓展求出 $d_i$,否则考虑在其它情况下字符串长什么样:
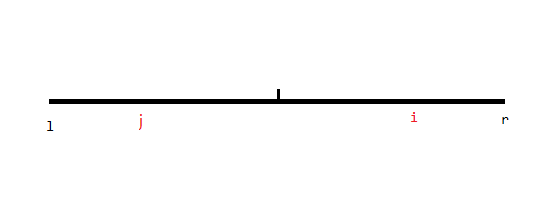
那么我们可以在回文区间 $[l,r]$ 对称的位置找到一个 $j$,那么容易想到 $d_i$ 很可能等于 $d_j$!
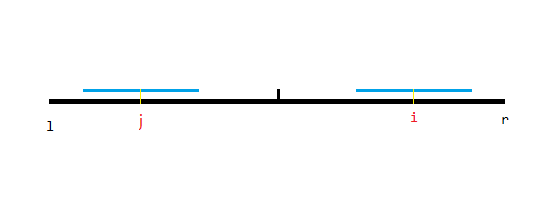
比如这种情况,假设 $d_j$ 对应的是左边蓝色区间,那么右边的蓝色区间显然与左边的完全相等(注意是回文的),且无法拓展(考虑定义中的最长)。
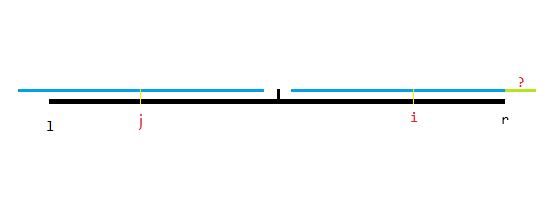
但是在这种情况,我们无法确定右边黑色区间外的绿色区间是否与左侧匹配。这种时候就要暴力拓展了。
容易发现,每次暴力拓展都会更新 $r$,而 $r$ 至多被拓展 $n$ 次,若不拓展 $r$ 那么是 $O(1)$ 求出 $d_i$ 的。故复杂度是 $O(n)$。
P3805 【模板】manacher 参考代码
const int N=1.1e7+5,inf=0x3f3f3f3f;
int n,d1[N],d2[N],ans;
char str[N];
signed main(){
scanf(" %s",str+1);
n=strlen(str+1);
int l=1,r=0;
forup(i,1,n){//长度为奇数
int k=(i>r)?1:min(d1[l+r-i],r-i+1);
while(1<=i-k&&i+k<=n&&str[i+k]==str[i-k]) ++k;
d1[i]=k--;
if(i+k>r){
l=i-k;r=i+k;
}
ans=max(ans,d1[i]*2-1);
}
l=1,r=0;
forup(i,1,n){//长度为偶数
int k=(i>r)?0:min(d2[l+r-i+1],r-i+1);
while(1<=i-k-1&&i+k<=n&&str[i-k-1]==str[i+k]) ++k;
d2[i]=k--;
if(i+k>r){
l=i-k-1;
r=i+k;
}
ans=max(ans,d2[i]*2);
}
printf("%d\n",ans);
}
但是其实有更简单的写法。考虑若回文子串长度为偶数,那么对称轴是两位置之间的间隔,那我们不妨把间隔用字符替代,这样对称轴就必定是某位置了。
比如原来字符串长这样:abbaabba
我们把间隔替换成字符:#a#b#b#a#a#b#b#a#
两侧的 # 是为了实现方便。
这样就只需要跑 $d_1$ 即可,另外,容易发现这样得到的 $d_i$ 等于以 $i$ 为中心的极长回文子串长度 $+1$。