网络流基础
前言
作为这个博客(时间上的)的第一个算法内容,我本来打算放一点我喜欢的(比如数论基础),但是最近教练勒令我们先自学一下网络流,那来都来了,网络流也是个很重要的内容,不如就先写这个了。
定义
学一个东西肯定要先了解它“是什么”,不然就会像我学 DP 一样学了两年没入门。
网络流的定义
- 网络的定义:
网络是指一个有向图 $G=(V,E)$。
每条边 $(u,v)\in E$ 都有一个权值 $c(u,v)$,称之为容量(Capacity),当 $(u,v)\notin E$ 时有 $c(u,v)=0$。
其中有两个特殊的点:源点(Source)$s\in V$ 和汇点(Sink)$t\in V$,($s\neq t$)。
- 流的定义
设 $f(u,v)$ 定义在二元组 ($u\in V,v\in V$) 上的实数函数且满足
- 容量限制:对于每条边,流经该边的流量不得超过该边的容量,即,$f(u,v)\leq c(u,v)$。
- 斜对称性:每条边的流量与其相反边的流量之和为 0,即 $f(u,v)=-f(v,u)$。
- 流守恒性:从源点流出的流量等于汇点流入的流量,即 $\forall x\in V-{s,t},\sum_{(u,x)\in E}f(u,x)=\sum_{(x,v)\in E}f(x,v)$,并且出去源汇外每个点的流入流量和流出流量相同。
那么 f 称为网络 G 的流函数。对于 $(u,v)\in E,f(u,v)$ 称为边的流量,$c(u,v)-f(u,v)$ 称为边的剩余容量。整个网络的流量为 $\sum_{(s,v)\in E}f(s,v)$,即 从源点发出的所有流量之和。
一般而言也可以把网络流理解为整个图的流量。而这个流量必满足上述三个性质,我们称满足这三个性质的流为可行流。
摘自 OI Wiki
网络流常见算法
常见的网络流问题有三种:最大流,最小割,费用流。但是一般都不会直接考,因为网络流的重点是建模(就是如何把一个问题转化为网络流问题 比如著名段子用网络流算 A+B problem),所以一般网络流题不会考你具体用哪个算法(但不排除有毒瘤出题人),通常我们三种问题各记一个算法就行了。
最大流
我们有一张图,要求从源点流向汇点的最大流量(即最大的源点流出流量),就是我们的最大流问题。
最大流是最基础的网络流问题,而解决最大流问题的入门算法有三种。
FF 算法
FF(Ford-Fulkerson)算法是解决最大流问题最基础的算法,其它算法基本都是以它为理论基础建立的。但它的复杂度并不优秀所以一般不掌握。
这个算法可以用一句话描述:
从任何的一个可行流开始,寻找增广路对网络进行增广,直到网络中不存在增广路径。
FF 算法的核心在于找增广路,何为增广路?
增广路的定义
增广路,是从源点到汇点的路径,其上所有边的残余容量均大于 $0$。FF 算法就是不断寻找增广路,直到找不到为止。
什么是残余容量?首先每条边最初的残余容量就是它的容量 $c(u,v)$,然后流了一段时间后,这条边的流量为 $f(u,v)$,那么这条边的残余流量就是 $c(u,v)-f(u,v)$。通俗来讲,残余容量就是一条边还能容纳多少流量。残余容量组成的网络叫残量网络。
FF 算法的过程就是每次找一条增广路,然后流满这条路的流量,一直到找不到为止。
那么,这个算法一定是对的吗? 明明都说了是最基础的算法怎么可能是错的。
确实不一定是对的。
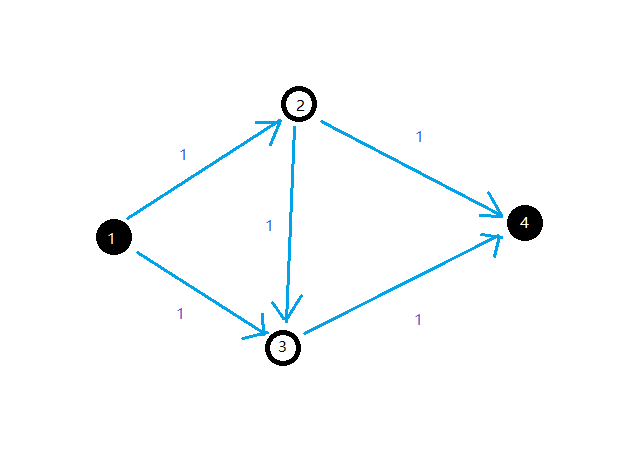
假如我们有这么一个网络,原点 $s=1$,汇点 $t=4$,要求它的最大流。
假如我们第一次找到增广路 $1 \to 2 \to 3 \to 4$,容易发现这样就找不到第二条增广路了。但实际上这张图可以有两条增广路为 $1 \to 2 \to 4$ 和 $1 \to 3 \to 4$。
为了解决这个问题,我们引入了反向边,来维护一个类似于“反悔”的过程。
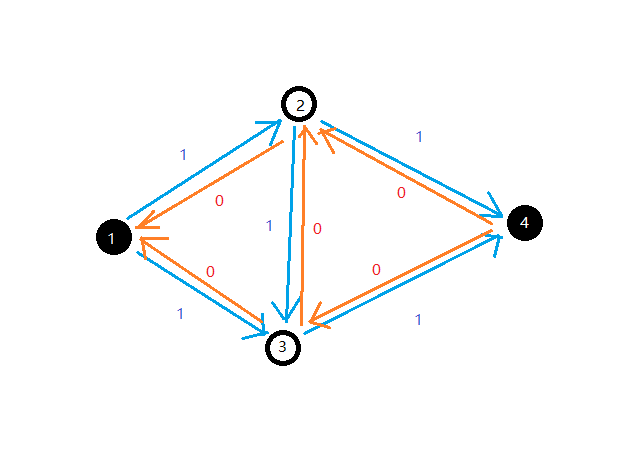
反向边 $(v,u)$ 的残量永远为 $f(u,v)$,即相应的正向边的流量。每次假如有流量经过反向边,那么相当于对对应正向边的流量做撤销操作。
比如上一张图,假如我们找到了一条流量为 $1$ 的增广路 $1 \to 2 \to 3 \to 4$,那么残量网络就会变成这样:
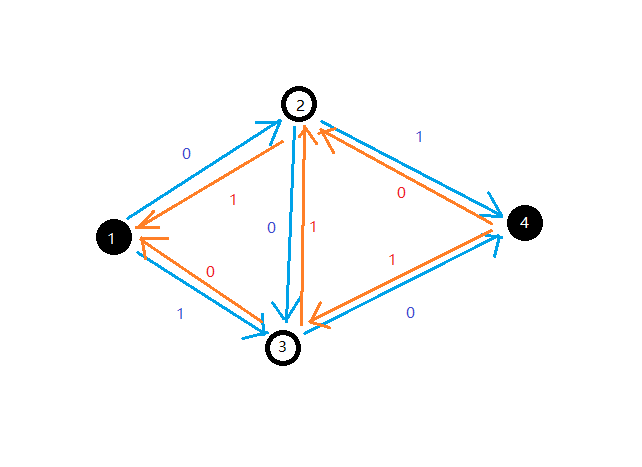
这时候我们就能找到另一条流量为 $1$ 的增广路 $1 \to 3 \to 2 \to 4$。
在程序眼里,我们走的两条增广路分别是 $1 \to 2 \to 3 \to 4$ 和 $1 \to 3 \to 2 \to 4$,其实我们自己分析一下会发现这样等价于走 $1 \to 2 \to 4$ 和 $1 \to 3 \to 4$,中间的 $3 \to 2$ 相当于撤销了 $2 \to 3$ 的流量。
这样建边后,一个非常重要的性质是当前流是最大流当且仅当不存在增广路。
证明
- 充分性(是最大流 $\Rightarrow$ 不存在增广路):
考虑逆否命题:若存在增广路则不是最大流。
显然,因为还能增加至少 $1$ 流量。
- 必要性(不存在增广路 $\Rightarrow$ 是最大流)
下面的证明和后文有关,初学者请忽略。
当不存在增广路时,显然在残量网络上 $s$ 不能到达 $t$。那么将 $s$ 能到达的点集视为 $S$,剩下的视为 $T$。就存在一个割 $(S,T)$。根据后文“最大流最小割定理”的引理,流小于等于割。显然这个割的容量恰好就是当前的流量。故当前为最大流。
值得一提的是,虽然在理论上反向边和正向边是不同的,实际在程序实现上它们并没有什么特别大的差异。
FF 算法参考代码
struct Flow{
struct edge{
int v,rst,nxt;
}e[M<<1];
int head[N],cnte=1;// (1)!
int n,s,t;
int vis[N];
void adde(int u,int v,int w){
e[++cnte]=edge{v,w,head[u]};head[u]=cnte;
e[++cnte]=edge{u,0,head[v]};head[v]=cnte;
}
int dfs(int x,int flow){
if(x==t){// (2)!
return flow;
}
vis[x]=true;
for(int i=head[x];i;i=e[i].nxt){
int v=e[i].v,w=e[i].rst;
if(w>0&&!vis[v]){
int c=dfs(v,min(flow,w));
if(c!=-1){
e[i].rst-=c;
e[i^1].rst+=c;// (3)!
return c;
}
}
}
return -1;// (4)!
}
i64 FF(){
i64 ans=0,c;
while((c=dfs(s,inf))!=-1){// (5)!
mem(vis,0);
ans+=c;
}
return ans;
}
}mf;
cnte一定要从 $1$ 开始,后面会解释(其实任何正奇数和 $-1$ 都可以,但是不能为 $0$)。- 如果增广路走到汇点直接返回流量。
- 因为
cnte从 $1$ 开始,又由于每条边和反向边是相邻的,所以每条边和其反向边相异或必定为 $1$。 - 无法到达汇点,返回 $-1$。
- 一直重复到找不到增广路为止。
FF 算法的复杂度上界为 $O(ef)$,其中 $e$ 为边数,$f$ 为最大流,证明显然,假设每次遍历所有边找到一条流量为 $1$ 的增广路。
在洛谷模板题上可以获得 $84pts$ 的高分。

EK 算法
EK(Edmond-Karp)算法的核心也是找增广路,只不过它是用 BFS 实现的。它可以保证每次找到的都是最短的增广路。
EK 算法参考代码
queue<int> q;
int pre[N],flow[N];
int bfs(){
mem(pre,-1);
while(q.size()) q.pop();
q.push(s);
flow[s]=inf;
while(q.size()){
int u=q.front();q.pop();
if(u==t) break;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v,w=e[i].rst;
if(w>0&&pre[v]==-1){// (1)!
pre[v]=i;
flow[v]=min(flow[u],w);
q.push(v);
}
}
}
return pre[t]!=-1;// (2)!
}
i64 EK(){
i64 ans=0;
while(bfs()){
ans+=flow[t];
for(int i=t;i!=s;i=e[pre[i]^1].v){// (3)!
e[pre[i]].rst-=flow[t];
e[pre[i]^1].rst+=flow[t];
}
}
return ans;
}
- 假如这条边还有残量并且 $v$ 没被访问过。
- 能否到达汇点。
- 从汇点出发更新残量。
EK 算法的复杂度上限为 $O(ve^2)$,其中 $v$ 为点数。证明可以参考这篇文章。这个算法已经能通过洛谷模板题了。

dinic 算法
事实上,dinic 算法才是广大 OIer 写最大流最常用的算法,据传言提高组出题人中有一个不成文的规定:出最大流题可以卡 EK 算法,但不能卡 dinic 算法。
dinic 算法结合了 FF 算法和 EK 算法的长处,考虑在增广时先用 BFS 对网络按与源点的距离分层,再用 DFS 寻找增广路。每次找增广路时只会往层数高一级的方向找,感性理解的话,这样不兜圈子也不走回头路,就会优化时间,严谨证明可以参考 OI Wiki。
另外 dinic 算法有两个优化,当前弧优化和多路增广。虽然这两个优化是本质不同的,当前弧优化是保证复杂度正确的优化而多路增广只是常数优化,但是由于互联网以讹传讹通常被称作 dinic 两大优化。
dinic 算法参考代码
int dpt[N],cur[N];
bool bfs(){
while(q.size()) q.pop();
forup(i,1,n){
cur[i]=head[i];// (3)!
dpt[i]=-1;
}
dpt[s]=0;
q.push(s);
while(q.size()){
int u=q.front();q.pop();
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(dpt[v]==-1&&e[i].rst){// (4)!
dpt[v]=dpt[u]+1;
q.push(v);
}
}
}
return dpt[t]!=-1;
}
int dfs(int x,int flow){
if(x==t||!flow) return flow;
int res=0;
for(int i=cur[x];i;i=e[i].nxt){// (1)!
cur[x]=i;int v=e[i].v;
if(dpt[v]==dpt[x]+1){
int get=dfs(v,min(flow-res,e[i].rst));
if(get){
res+=get;
e[i].rst-=get;
e[i^1].rst+=get;
if(res==flow) break;// (2)!
}
}
}
return res;
}
i64 dinic(){
i64 ans=0;
while(bfs()){
ans+=dfs(s,inf);
}
return ans;
}
- 当前弧优化,假设(在当前分层方法下)某条边已经跑满了,那后面它必不可能成为增广路中的边,我们可以复制一份
head数组(即本代码中的cur数组)来存储第一条还有残量的边。 - 多路增广,只有在没有剩余流量时才退出,假如 $s \to x$ 还有剩余流量就继续找增广路尽可能把流量流完。
- 注意每次循环都要更新层数和
cur数组,因为在不同的残量网络上分层可能不同。 - 如果这条边还有残量且下一个点没被访问过。
dinic 的复杂度上界是 $O(v^2e)$,但是据 OI Wiki 说基本不可能卡到这个上界,在提高组范围内可以看做 $O(\text{能过})$。
在洛谷模板题上跑得飞快。

关于 dinic 的复杂度问题
此段更新于 2024.6.4。
好嘛,现在不是提高组范围了,我们来考虑一下复杂度的证明。
dinic 复杂度由两部分构成,每次增广复杂度 $O(nm)$,增广轮数上界 $O(n)$,复杂度 $O(n^2m)$。
-
每轮增广复杂度证明:
考虑每次会花至多 $O(n)$ 的时间找到一条路径,它要么是增广路,那么其中饱和边的 $cur$ 会跳转。要么因为结尾被阻塞而不是增广路,那么路径末端的 $cur$ 会跳转。每找到一条路径 $cur$ 都会跳转一次,最多跳转 $m$ 次,于是每次增广复杂度是 $O(nm)$ 的。
-
增广轮数上界证明:
当前层次图增广完成后,$s\rightsquigarrow t$ 的最短路必定会经过至少一条不在层次图上的边(不然就还能再增广),不在层次图上的边必定会指向同一层或者更底层的边,那么这条路径长度至少会增加 $1$,于是至多增加 $n$ 次,所以是 $O(n)$ 的。
与值域相关的复杂度上界(在某些特殊图上的复杂度)
阅读此段前,请确保你已经了解了割的定义。
- 单位容量网络中,单轮增广复杂度为 $O(m)$。
证明:一条边无论有没有流都会跳转当前弧,那么单轮增广每条边都只会被访问一次。
- 单位容量网络中,增广轮数不超过 $O(\sqrt{m})$。
证明:增广 $\sqrt{m}$ 轮后,层次图至少有 $\sqrt{m}$ 层,根据抽屉原理,至少存在一个 $i$ 使得 $i$ 到 $i+1$ 层的边数不超过 $\sqrt{m}$,且这显然是一个割,那么剩下的残量网络最大流不会超过 $\sqrt{m}$(根据下文最大流最小割定理),那么至多再增广 $\sqrt{m}$ 轮。
- 无重边的单位容量网络中,增广轮数不超过 $O(n^{\frac{2}{3}})$。
证明:类似吧,增广 $2n^{\frac{2}{3}}$ 轮后,层次图至少有 $2n^{\frac{2}{3}}$ 轮,每相邻两层分一组,根据抽屉原理,至少有一组组内点数不超过 $n^{\frac{1}{3}}$,那么该组内边数不超过 $n^{\frac{2}{3}}$,则至多再增广 $O(n^{\frac{2}{3}})$ 轮。
- 任意网络中,设 $C$ 为容量总和,复杂度不会超过 $O(C\sqrt{C})$。
证明:肯定不会比拆成一条一条的单位网络更劣。
- 任意网络中,增广轮数不超过 $O(\sqrt{S})$。
用 $in_u,out_u$ 分别代表 $u$ 入边和出边的容量和,其中 $S=\sum_{u\in V\setminus\begin{Bmatrix}s,t\end{Bmatrix}}\min(in_u,out_u)$
证明:增广 $\sqrt{S}$ 轮后,除源汇以外的点 $in_u,out_u$ 均不变(考虑增广路进入这个点和走出这个点的边相互抵消),此时增广路至少有 $\sqrt{S}$ 层,那么残量网络每单位流至少经过 $\sqrt{S}$ 个点,而所有点能经过的流总数不超过 $S$,于是残量网络的最大流不超过 $\sqrt{S}$,至多再增广 $\sqrt{S}$ 轮。
- 任意网络中,加了多路增广的 dinic 复杂度不超过 $O(np+nm)$,其中 $p$ 是增广路条数总和。
证明:
考虑之前的复杂度证明中有这么一句话:
每次会花至多 $O(n)$ 的时间找到一条路径。
但是根据刚才的几次分析,容易发现每次至多会花 $O(d)$(其中 $d$ 是层次图层数)的时间找到一条路。并且如果用了多路增广,相当于遇到阻塞流后只花了 $O(1)$ 的时间就找到了下一条路径,也就是说只花了 $O(1)$ 的时间就使 $cur$ 跳转了一下。
那么每一轮增广的复杂度上界为 $O(d\times t+m)$,其中 $d$ 为层次图层数,$t$ 为形成阻塞流的增广路条数。
那么总复杂度不超过 $O(np+nm)$,其中 $p$ 是增广路总数,因为每条增广路若形成阻塞流会贡献至多 $n$ 的复杂度,否则会算到后面的 $m$ 里。后面的 $nm$ 是好理解的。
- 任意网络中,总复杂度不超过 $O(mf)$,其中 $f$ 为最大流流量。
证明:增广路总条数和增广轮数均不超过 $f$,加上结论 $6$ 可以推出应是 $O(nf+mf)$。又由于 $n\le m$,于是 $O(mf)$。
- 任意网络中,总复杂度不会超过 $O(mS^{\frac{2}{3}})$,$S$ 定义见上文。
证明:增广 $S^{\frac{1}{3}}$ 轮后层次图层数至少为 $S^{\frac{1}{3}}$,这一部分每一轮复杂度为 $O(mS^{\frac{1}{3}})$,于是总复杂度为 $O(mS^{\frac{2}{3}})$。残量网络中,每条增广路至少经过 $S^{\frac{1}{3}}$ 个点,与之前的同理,残量网络的最大流不超过 $S^{\frac{2}{3}}$,根据结论 $7$,剩下的复杂度为 $O(mS^{\frac{2}{3}})$。
- 任意网络中,总复杂度不会超过 $O(\sqrt[3]{n^2mS^2}+m\sqrt{S})$。
妈的怎么越来越复杂了。
证明:
设一个阈值 $B$,先增广 $B$ 轮,此时层次图轮数至少为 $B$,复杂度为 $O(mB^2)$,此时残量网络最大流不会超过 $\frac{S}{B}$,又因为最多增广 $O(\sqrt{S})$ 轮,根据结论 $6$ 剩下的时间复杂度为 $O(\frac{nS}{B}+m\sqrt{S})$。
二者相加,得复杂度为 $O(mB^2+\frac{nS}{B}+m\sqrt{S})$。取 $B=O(\sqrt[3]{\frac{nS}{m}})$,得复杂度为 $O(\sqrt[3]{n^2mS^2}+m\sqrt{S})$。
- 总结:
设 $c$ 为单条边的容量上界,不难发现有 $S\le C\le mc$。
| 通式 | $O(C\sqrt{C})$(结论 $4$) | $O(nm\sqrt{S})$(结论 $5$) | $O(\sqrt[3]{n^2mS^2}+m\sqrt{S})$(结论 $9$) |
|---|---|---|---|
| 用 $c$ 表示 | $O(mc\sqrt{mc})$ | $O(nm\sqrt{mc})$ | $O(m(\sqrt[3]{n^2c^2}+\sqrt{mc}))$ |
| $n,m,c$ 同阶(稀疏图) | $O(n^3)$ | $O(n^3)$ | $O(n^{\frac{7}{3}})$ |
| $n,c$ 同阶(稠密图,$m\approx n^2$) | $O(n^{\frac{9}{2}})>O(n^2m)$ | $O(n^{\frac{9}{2}})>O(n^2m)$ | $O(n^{\frac{7}{2}})$ |
最小割
在最小割之前,我们先讲讲割的定义。
割的相关概念
- 定义
对于一个网络流图 $G=(V,E)$,其割的定义为一种点的划分方式:将所有的点划分为 $S$ 和 $T=V-S$ 两个集合,其中源点 $s\in S$,汇点 $t\in T$。
- 割的容量
我们的定义割 $(S,T)$ 的容量 $c(S,T)$ 表示所有从 $S$ 到 $T$ 的边的容量之和,即 $c(S,T)=\sum_{u\in S,v\in T,(u,v)\in E}c(u,v)$。当然我们也可以用 $c(s,t)$ 表示 $c(S,T)$。
- 最小割
最小割就是求得一个割 $(S,T)$ 使得割的容量 $c(S,T)$ 最小。
摘自 OI Wiki。
如何求最小割呢?我们有一个非常强的定理。
最大流最小割定理
这个定理的内容非常简单:最大流等于最小割。
证明
形式化地,$f_{\max}(s,t)=c_{\min}(s,t)$
对于任意一个可行流 $f(s,t)$ 的任意一个割 $(S,T)$,我们可以得到:
$$f(s,t) = \sum_{u\in S, v\in T,(u,v)\in E}f(u,v)-\sum_{u\in T, v\in S,(u,v)\in E}f(u,v)$$
就是从 $s$ 到 $t$ 的总量等于流过去的减去流回来的。
由于可行流的性质,上面这玩意儿显然小于等于 $\sum_{u\in S,v\in T,(u,v)\in E}c(u,v)$,所以流小于等于割。
将网络跑出最大流后,可以构造出一个割:把 $s$ 能通过残量网络到的点集设为 $S$,其余设为 $T$, 作为割 $(S,T)$, 从 $S$ 到 $T$ 的边必然满流, 从 $T$ 到 $S$ 的边必然 $0$ 流, 所以这个割的容量就是最大流的流量,根据流小于等于割这个割就是最小割。
由于 $s$ 能通过残量网络到的点集为 $S$,所以 $S$ 到 $T$ 显然满流,那么 $T$ 到 $S$ 为什么必定 $0$ 流呢? 这不是显然吗 但并没有这样一个定理。我们可以用反证法,假设有一条从 $T$ 到 $S$ 的边不 $0$ 流,即 $f(u\in T,v\in S)> 0$,那么对于它的反向边 $(v,u)$,有 $f(v,u)<c(v,u)$,即 $(v,u)$ 不满流,与假设 $u \in T,v\in S$ 矛盾,故从 $T$ 到 $S$ 的边必定 $0$ 流。
所以求最小割也是跑一遍 dinic 就行了,甚至还能算出方案,只要遍历一下在残量网络上 $s$ 能到达的所有结点即可。
必割边与可行边
在有些时候,最小割题会需要你求出满足某些条件的割边(或其存在性)。这种时候就需要知道在最小割中哪些边是必须割的,哪些边是可以割的。下面所有条件都是在跑完最大流的残量网络上叙述的。
可行边
$u\to v$ 是可行边的必要条件: 1. 满流 2. 在残量网络中找不到 $u\rightsquigarrow v$ 的路径。
首先不满流显然不能割,根据最小割性质所有割边必须满流。
另一个条件考虑证必要性,若 $u\to v$ 是割边,且存在 $u\rightsquigarrow v$ 的路径,又由于不存在增广路(最大流已经跑完),残量网络上每条边均固定,那么无论怎么分 $u\rightsquigarrow v$ 路径上的点,残量网络上都至少会有一条 $S\to T$ 的边,不满足割的性质。
另一种理解是假如退掉若干流量,那么这些流量可以不走这条边补回来。
具体求法可以考虑跑 SCC。若 $u$ 能到 $v$ 那么 $u,v$ 就在同一个强连通分量里面(因为残量网络上有 $v\to u$ 的边)。
必割边
$u\to v$ 是必割边的充要条件: 1. 满流 2. 残量网络上 $s$ 能到 $u$,$v$ 能到 $t$。
容易发现这个条件严格包含“可行边”的条件(不然就有增广路)。
增大此边后最小割必定会变大,说明最小割必定包含这条边。
最大权闭合子图
此段为 2024.1.31 更新。
起因是在专题里面找到一道题,归约成了看起来能用最小割做的样子,但不知道怎么建模。询问 LCX 后得知是板,遂学习。
问题描述:给定一个点带权(有正有负)的有向图 $G=\begin{Bmatrix}V,E\end{Bmatrix}$,求出一个子图 $G'=\begin{Bmatrix}V',E'\end{Bmatrix}(V'\subseteq V,E'\subseteq E)$,满足 $\forall (u,v)\in E$,若 $u\in V'$,则 $v\in V'$(我们称这样的图为闭合子图,其实就是从某一些点开始能走到的所有点)。最大化集合 $V'$ 的点权和。
直接给出建模:
- $\forall (u,v)\in E$,连边 $(u,v,+\inf)$。
- $\forall u,val_{u}\ge 0$,连边 $(s,u,val_u)$。
- $\forall u,val_{u}< 0$,连边 $(u,t,-val_u)$。
然后最大权闭合子图权值和就是正权点点权和减去最小割。对应结点就是与 $s$ 连通的部分。
正确性证明
由于最小割的性质,除去割边以外,和 $s$ 相连的那一个部分不能有边指向另一个部分,又由于能割掉的边只有与 $s,t$ 相连的边,因为中间的边权为正无穷,显然与 $s$ 相连的必定是闭合子图。
假设一开始所有正权点都在闭合子图中,若割掉某正权点与 $s$ 的连边,说明它被踢出了闭合子图,权值减小 $val_u$。对于负权点,若割掉与 $t$ 的连边说明它被加入了闭合子图。
故最大权闭合子图权值和就是正权点点权和减去最小割。
另外最大权闭合子图建模还有一些技巧:
最大权闭合子图建模技巧
- 钦定选/不选某个点
考虑新建两个点 $\inf,-\inf$,点权分别为正充分大值和负充分大值。
如果必须选一个点,那么将它连在 $\inf$ 后面,因为 $\inf$ 这个点是必选的。
如果必须不选某个点。那么将它连向 $-\inf$ 后面。因为 $-\inf$ 是必不选的,所以不能选它。
- 最小权闭合子图
其实就是全部取反后建模再把答案取反。但如果答案是非负的这样会求出空子图。这时候应该考虑你是不是有一些必选的点,然后用上面的方法钦定它。
最小割树(Gomory-Hu Tree)
此段为 2024.5.6 更新。
最小割怎么这么多神秘引申算法。
容易发现 dinic 一次只能求两点间的最小割,但如果有多组询问就寄了,然后就有神秘选手发明了能解决最小割多组询问的神秘算法,即最小割树(Gomory-Hu Tree)。
- 核心性质
对于图 $G$,构造一棵树 $T$,使得任意两点间在原图上的最小割就是树上两点间路径上的边权最小值。
- 如何构造
图中只有一个点时,最小割树就是单独这个点。否则任意选取两个不同的点,求出在原图上的最小割,在最小割树中的这两点间连上边权等于最小割容量的边,并根据最小割与当前集合的交划分出两个集合,递归在两个集合内进行构造。总共求 $n−1$ 次最小割,恰好连 $n-1$ 条边。
- 正确性证明
妈的网上找的免费内容没有一篇证明正确性的。还好有学长的课件。
考虑归纳法,归纳证明任一点集 $R$ 都满足性质。为方便叙述,设 $u,v$ 间最小割容量为 $c(u,v)$,两点集 $S,T$ 中间的边权容量和表示为 $f(S,T)$。
当 $|R|=1$,显然满足性质。
当 $|R|\ne 1$,假设递归的两集合 $S,T$ 都是满足性质的。那么对于一点对 $(u,v)$,若 $u,v\in S$,则可直接套用 $S$ 部分的结论。$u,v\in T$ 同理。下面单独讨论 $u\in S,v\in T$ 的情况。
设本层分治选取的点为 $s\in S,t\in T$,则 $u,v$ 在最小割树上的路径为 $u\rightsquigarrow s \to t \rightsquigarrow v$,由于 $S,T$ 内部结论均成立,故此时路径上权值的最小值为 $\min\begin{Bmatrix}c(u,s),c(s,t),c(t,v)\end{Bmatrix}$。
那么考虑证明 $c(u,v)=\min\begin{Bmatrix}c(u,s),c(s,t),c(t,v)\end{Bmatrix}$,先考虑 $c(s,t)$ 的贡献
引理
引理:$\forall a,b,c(a\ne b\ne c)$ 必然有 $c(a,b)\ge \min[c(a,c),c(c,b)]$
证明:
考虑反证法,假设 $\exists a,b,c,$ 使得 $c(a,b)< \min[c(a,c),c(c,b)]$。
那么对于 $c(a,b)$,设对应两集合分别是 $A,B$。
若 $c\in A$,则 $(A,B)$ 也是 $c,b$ 的一个割,故 $c(c,b)=c(a,b)$。
若 $c\in A$,同理。
则此时 $c(a,b)= \min[c(a,c),c(c,b)]$,与假设矛盾。
综上,$c(a,b)\ge \min[c(a,c),c(c,b)]$。
由引理得 $c(u,v)\ge \min[c(u,t),c(t,v)]\ge \min\begin{Bmatrix}c(u,s),c(s,t),c(t,v)\end{Bmatrix}$,则当 $c(s,t)$ 产生贡献时必然正确。
然后考虑 $c(u,s)$ 和 $c(t,v)$,考虑这样的构造:
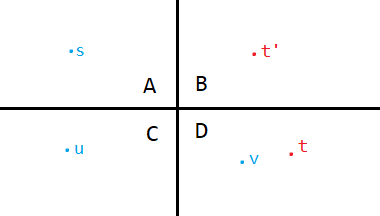
设 $s,u$ 的最小割为 $(A \cup B,C\cup D)$,$s,t$ 的最小割为 $(A\cup C,B\cup D)$,若 $t\in D$,则 $s,t$ 的最小割也是 $s,u$ 的割,此时 $c(s,t)<c(s,u)$,$c(s,u)$,不会产生贡献。
若 $t'\in B$,则 $(A\cup C\cup D,B)$ 也是一个 $s,t'$ 的割,又由于 $s,t'$ 的最小割为 $(A \cup B,C\cup D)$,有:
$$f(A,B)+f(A,D)+f(C,B)+f(C,D)\le f(A,B)+f(C,B)+f(D,B)$$
故 $f(A,D)+f(C,D)\le f(D,B)$。对于 $s,u$ 同理可得 $f(A,D)+f(B,D)\le f(C,D)$。两式联立可得 $f(A,D)=0,f(C,D)=f(B,D)$。那么此时 $(A\cup B\cup D,C)$ 就是 $s,u$ 的最小割。又由于它也是 $(u,v)$ 的割,故 $c(u,v)\le c(s,u)$。
同理可证:$c(u,v)\le c(s,u)$(前提是 $c(s,t)$ 不产生贡献)。
综上,若 $c(s,t) \le c(s,u),c(t,v)$,此时 $c(u,v)\le c(s,t)$,且 $c(u,v) \ge c(s,t)$。故 $c(u,v)=c(s,t)$。
若 $c(s,t)$ 不是三者中的最小值,那么若 $c(s,u)\le c(t,v)$,则 $c(u,v)\ge c(s,u)$ 且 $c(u,v)\le c(s,u)$,此时 $c(u,v)=c(s,u)$,$c(s,u)>c(t,v)$ 时同理。
故 $c(u,v)=\min\begin{Bmatrix}c(u,s),c(s,t),c(t,v)\end{Bmatrix}$,得证。
这样我们就证明了 $|R|\ne 1$ 时性质仍成立,故这样构造是正确的。
复杂度是 $O(n^3m)$(dinic 复杂度乘以 $n$)。
模板题参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
#ifdef DEBUG
#define msg(args...) fprintf(stderr,args)
#else
#define msg(...) void()
#endif
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=505,inf=0x3f3f3f3f;
int n,m;
namespace flow{
struct edge{
int v,rst,nxt,pw;
}e[N*8];
int head[N],cur[N],dpt[N],s,t,cnte=1,vis[N];
void clear(int _s,int _t){
s=_s;t=_t;
forup(i,1,cnte){
e[i].rst=e[i].pw;
}
mem(vis,0);
}
void adde(int u,int v,int w){
e[++cnte]=edge{v,w,head[u],w};head[u]=cnte;
e[++cnte]=edge{u,w,head[v],w};head[v]=cnte;
}
bool bfs(){
queue<int> q;
forup(i,1,n){
dpt[i]=-1;
cur[i]=head[i];
}
q.push(s);dpt[s]=0;
while(q.size()){
int u=q.front();q.pop();
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(!e[i].rst||dpt[v]!=-1) continue;
dpt[v]=dpt[u]+1;
q.push(v);
}
}
return dpt[t]!=-1;
}
int dfs(int x,int flow){
if(x==t||!flow) return flow;
int res=0;
for(int i=cur[x];i;i=e[i].nxt){
cur[x]=i;
int v=e[i].v,rst=e[i].rst;
if(dpt[v]!=dpt[x]+1||!rst) continue;
int gt=dfs(v,min(rst,flow-res));
if(gt){
res+=gt;
e[i].rst-=gt;
e[i^1].rst+=gt;
if(res==flow) break;
}
}
return res;
}
int dinic(){
int ans=0;
while(bfs()){
ans+=dfs(s,inf);
}
return ans;
}
void dfs1(int x){
vis[x]=1;
for(int i=head[x];i;i=e[i].nxt){
if(vis[e[i].v]||!e[i].rst) continue;
dfs1(e[i].v);
}
}
}
struct edge{
int v,w;
};
vector<edge> e[N];
int a[N];
void build(int l,int r){
if(l>=r) return;
flow::clear(a[l],a[l+1]);
int f=flow::dinic();
e[a[l]].push_back(edge{a[l+1],f});
e[a[l+1]].push_back(edge{a[l],f});
flow::dfs1(flow::s);
vector<int> v1,v2;
forup(i,l,r){
if(flow::vis[a[i]]){
v1.push_back(a[i]);
}else{
v2.push_back(a[i]);
}
}
int pl=l;
for(auto i:v1) a[pl++]=i;
for(auto i:v2) a[pl++]=i;
build(l,l+v1.size()-1);
build(l+v1.size(),r);
}
int f[10][N],g[10][N],dpt[N];
void dfs(int x,int fa){
f[0][x]=fa;dpt[x]=dpt[fa]+1;
forup(i,1,9){
f[i][x]=f[i-1][f[i-1][x]];
g[i][x]=min(g[i-1][x],g[i-1][f[i-1][x]]);
}
for(auto i:e[x]){
if(i.v==fa) continue;
g[0][i.v]=i.w;
dfs(i.v,x);
}
}
int Query(int x,int y){
if(dpt[x]>dpt[y]) swap(x,y);
int res=inf;
for(int i=9;i>=0&&dpt[y]>dpt[x];--i){
if(dpt[f[i][y]]>=dpt[x]){
res=min(res,g[i][y]);
y=f[i][y];
}
}
if(x==y) return res;
for(int i=9;i>=0&&f[0][x]!=f[0][y];--i){
if(f[i][x]!=f[i][y]){
res=min(res,g[i][x]);
res=min(res,g[i][y]);
x=f[i][x];y=f[i][y];
}
}
res=min(res,g[0][x]);
res=min(res,g[0][y]);
return res;
}
mt19937 mr(time(0));
signed main(){
n=read();m=read();
forup(i,1,n) a[i]=i;
shuffle(a+1,a+n+1,mr);
forup(i,1,m){
int u=read(),v=read(),w=read();
flow::adde(u,v,w);
}
build(1,n);
dfs(1,0);
int q=read();
forup(i,1,q){
int u=read(),v=read();
printf("%d\n",Query(u,v));
}
}
平面图上最小割的快速求法
右转平面图性质。
费用流
费用流,全称最小费用最大流。我们学最大流时或多或少都会意识到一个网络取到最大流的流不止一个。再某些问题上,网络上的边会有使用代价(比如现实中自来水引水之类的问题),我们需要一种算法来解决在流量等于最大流的情况下,最小化费用的问题。
形式化地,给定一个网络 $G=(V,E)$,每条边除了容量限制 $c(u,v)$,还有一个单位费用 $w(u,v)$,当 $(u,v)$ 的流量为 $f(u,v)$ 时,需要花费 $f(u,v)\times w(u,v)$ 的代价。
则在该网络中总花费最小的最大流称为最小费用最大流,即在最大化 $\sum_{(s,v)\in E}f(s,v)$ 的前提下最小化 $\sum_{(u,v)\in E}f(u,v)\times w(u,v)$。
然后反向边的费用为 $w(v,u)=-w(u,v)$,如果你理解了建反向边的意义这是显而易见的。
用类似的算法还能求解最大费用最大流,方法是把费用取相反数。
消圈定理
一个流是该流量下的最小费用流当且仅当残量网络无负圈。
正确性证明
- 必要性:
即“是最小费用流” $\Rightarrow$ “无负圈”。
考虑逆否命题,容易发现若有负圈,当前的流加上负圈会得到更小费用的流,并且流量不变。
- 充分性:
即“无负圈” $\Rightarrow$ “是最小费用流”。
仍然考虑逆否命题,若有更小费用的流,那么当前边权和最大的一条增广路的反向边在残量网络上除去和它的重边后必定会剩下至少一个负环。
SSP 算法
容易发现找增广路的具体顺序不影响最终最大流具体是多少,这就是 SSP(Successive Shortest Path)算法的核心思路。SSP 算法是一个贪心的算法,它的思路是每次找总的单位费用最小的增广路进行增广,从而使最大流更容易取到最小费用。
注意如果网络上存在单位费用为负的圈,SSP 算法无法正确求出最小费用最大流,但常见的问题通常不会出现负环,所以一般 SSP 就够用了。
SSP 算法正确性证明
我们考虑使用数学归纳法与反证法。
假设流量为 $i$ 最小费用为 $w_i$,由于图上没有负圈,所以 $w_0$ 只有一种取值为 $0$。
假如现在费用为 $w_i$,我们找到了一条单位费用总和最小的增广路并增加了 $1$ 流量,那么新的费用就是 $w_{i+1}$,说明这条增广路的单位费用总和为 $w_{i+1}-w_{i}$。
假如存在 $w_{i+1}'<w_{i+1}$,那么肯定存在一条增广路单位费用为 $w_{i+1}'-w_i<w_{i+1}-w_i$,与之前的“单位费用最小”矛盾,故 $w_{i+1}$ 为流量为 $i+1$ 的最小费用。
证毕。
一个更聪明的证法是考虑任意一条大于最短路的路径如果流过后它的反向边在残量网络上都会和最短路形成负环。
实现非常自然,只要把 dinic 中的 BFS 分层换成 Bellman–Ford 或者 SPFA 即可。
Bellman-Ford + dinic 参考代码
int dis[N],cur[N],cst,vis[N];
bool bellman(){
forup(i,1,n){
cur[i]=head[i];
}
mem(dis,0x3f);mem(vis,0);
dis[s]=0;
forup(i,1,n){
bool flag=false;
forup(u,1,n){
if(dis[u]==inf) continue;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v,w=e[i].w,c=e[i].c;
if(c==0) continue;
if(dis[v]>dis[u]+w){
dis[v]=dis[u]+w;
flag=true;
}
}
}
if(!flag) break;// (1)!
}
return dis[t]!=inf;
}
int dfs(int x,int flow){
if(x==t||!flow) return flow;
vis[x]=true;
int res=0;
for(int i=cur[x];i;i=e[i].nxt){
cur[x]=i;int v=e[i].v,w=e[i].w;
if(vis[v]) continue;// (2)!
if(dis[v]==dis[x]+w){
int get=dfs(v,min(flow-res,e[i].c));
if(get){
res+=get;
cst+=get*w;
e[i].c-=get;
e[i^1].c+=get;
if(res==flow) break;
}
}
}
return res;
}
pii SSP(){
int ans=0;
while(bellman()){
ans+=dfs(s,inf);
}
return mkp(ans,cst);
}
- 如果没有可以松弛的边直接结束。
- 注意反向边是负边权的所以只判
dis[v]==dis[x]+w会死循环,所以在费用流中 dinic 相对 EK 算法没什么优势(但也没什么劣势就对了)。
然后 Bellman-Ford 过不了洛谷模板题/kk。

考虑使用 SPFA。
SPFA 参考代码
queue<int> q;
bool spfa(){
forup(i,1,n){
cur[i]=head[i];
}
mem(dis,0x3f);mem(vis,0);
dis[s]=0;
while(q.size()) q.pop();
q.push(s);vis[s]=1;
while(q.size()){
int u=q.front();q.pop();
vis[u]=0;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v,w=e[i].w;
if(e[i].c&&dis[v]>dis[u]+w){
dis[v]=dis[u]+w;
if(!vis[v]){
q.push(v);
vis[v]=1;
}
}
}
}
mem(vis,0);// (1)!
return dis[t]!=inf;
}
- 注意在 dfs 前再次清空 vis 数组。
能过模板题。

如果用 Bellman-Ford 求解,每次找增广路的复杂度是 $O(nm)$ 的,故复杂度上界是 $O(nmf)$,如果用 SPFA 就是 $O(nkf)$ 的, 可以证明 $k$ 通常不大于 $2$。
另外一个常数更小的写法是使用 EK 而非 dinic,复杂度上界不变,而且看起来没那么铸币。
参考代码
自留复制板子用。
namespace flow{
const int N=5005,M=50005;
struct edge{
int v,rst,w,nxt;
}e[M<<1];
int head[N],incf[N],dis[N],pre[N],vis[N],cnte=1,s,t;
void adde(int u,int v,int rst,int c){
e[++cnte]=edge{v,rst,c,head[u]};head[u]=cnte;
e[++cnte]=edge{u,0,-c,head[v]};head[v]=cnte;
}
bool spfa(){
queue<int> q;
forup(i,1,n){
dis[i]=inf;
}
incf[t]=-1;incf[s]=inf;
q.push(s);dis[s]=0;vis[s]=1;
while(q.size()){
int u=q.front();q.pop();
vis[u]=0;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v,rst=e[i].rst,w=e[i].w;
if(!rst||dis[v]<=dis[u]+w) continue;
dis[v]=dis[u]+w;
incf[v]=min(incf[u],rst);
pre[v]=i;
if(!vis[v]){
q.push(v);
vis[v]=1;
}
}
}
return ~incf[t];
}
pii SSP(){
int mnc=0,mxf=0;
while(spfa()){
mxf+=incf[t];
for(int i=t;i!=s;i=e[pre[i]^1].v){
mnc+=incf[t]*e[pre[i]].w;
e[pre[i]].rst-=incf[t];
e[pre[i]^1].rst+=incf[t];
}
}
return mkp(mxf,mnc);
}
}
Primal-Dual 原始对偶算法
众所周知 Bellman-Ford 的复杂度为 $O(nm)$,SPFA 也能被卡到 $O(nm)$,在稀疏图和稠密图上都比不上优先队列优化的 Dijkstra 算法 $O(m \log m)$ 的复杂度,但假如一张图上存在负边权的边就不得不用。
而在图论中,有一个叫 Johnson 全源最短路的算法,它求解全源最短路只跑一遍 SPFA,通过给每个点设置势能使得边权全变为正,然后用 Dijkstra 求解,这种算法效率非常高,是 $O(nm\log m)$ 的。
而在费用流中,我们同样需要多次求解最短路,是否有类似的算法呢?答案是肯定的:Primal-Dual 原始对偶算法(简称原始对偶算法)。
首先跑一遍 SPFA 算出源点到每个点的初始距离 $h_i$ 作为改点的初始势能,接下来把每条边边权 $w(u,v)$ 重置为 $w(u,v)+h_u-h_v$,这样所有边权都变为非负的并且最短路一定对应原图的最短路,证明可以参考 OI Wiki,或者我未来的最短路文章。
注意到一个问题,每轮增广后残量网络的形态会变化,相应的,势能也应该变化。但我们不可能重新跑一遍 SPFA 不然那还不如 SSP 算法 。那具体如何更新呢?设增广后源点到 $i$ 号点的距离为 $d_i$(就是跑 Dijkstra 时求出来的),只需给 $h_i$ 加上 $d_i$ 即可。
正确性证明
首先容易发现这样仍会使最短路对应原图的最短路,对势能分析即可。
然后证明边权非负。
首先这轮增广后,由于可能有一些增广前 $f(i,j)=0$ 在增广路上,残量网络上就会多出一些 $(j,i)$ 的边,一定会满足 $d_j=d_i+w(i,j)+h_i-h_j$,不然 $(i,j)$ 就不在会增广路上了,故 $w(i,j)+(h_i+d_i)-(h_j+d_j)=0$,非负。
对于原有的边,$d_i+w(i,j)+h_i-h_j \ge d_j$,这由最短路“最短”的性质可以得到。故 $w(i,j)+(h_i+d_i)-(h_j+d_j) \ge 0$,同样非负。
故可以用 Dijkstra 算法正确地求出最短路。
关于值域问题,势能 $h_u$ 的值域与原边权 $s$ 到 $u$ 的最短路 $d_u$ 值域相同。始终有 $h_s=0$, 证明考虑重置边权后每条边边权非负,$h_s+d_u−h_u \ge 0$,那么 $h_u ≤d_u$。
原始对偶算法 +dinic 参考代码
- 先初始化势能。
- 每次更新势能。
- 一定要记得清空
vis数组。
但其实费用流写 EK 要好一点。
跑得快了不少。

但实际上费用流题一般不会卡你 SPFA,所以其实 SSP 就够用了。
上下界网络流
此段更新于 2024.6.7。
他娘的,网络流还在追我。
这个就不贴代码了,因为具体写法太多了。
上下界网络流就是一般的网络流对每条边流量的限制从“小于等于容量 $c$”改为了“大于等于 $l$ 小于等于 $r$”。
无源汇上下界可行流/最小费用可行流
给定无源汇流量网络 $G$,询问是否存在一种给每条边定容量的方式使得每条边容量在 $[l,r]$ 中,且每个点流入的容量与流出的容量相同。
不妨先假设最初 $f(u,v)=l(u,v)$,再设每条边容量 $c(u,v)=r(u,v)-l(u,v)$,加上超级源汇点就能转化为我们熟悉的“初始流量为 $0$”的问题了。但是这张新图上的可行流直接加上 $l(u,v)$ 后显然不一定是可行流,考虑对它进行一些调整。
现在考虑一个点,设它初始流入流量减去流出流量等于 $M$
- $M=0$,显然这个点它流量平衡,不额外连边。
- $M>0$,这个点流入的大于流出的,新图上可行流直接加上 $l(u,v)$ 会导致这个点流入大于流出,所以要构造使得这个点流出流量多 $M$,那么超级源点 $S$ 向这个点连容量为 $M$ 的边。
- $M<0$,同理,这个点向超级汇点 $T$ 连流量为 $-M$ 的边。
显然,上面第二种情况连边流量和与第三种边的流量和相等,证明考虑每条边的流量对总流出量和总流入量的贡献相同。
于是求出 $S\rightsquigarrow T$ 的最大流,如果与 $S$ 的连边恰好满流(显然此时与 $T$ 的连边也满流),就有解。并且原图上每条边的流量就是新图上流量加上 $l(u,v)$。
最小费用可行流就把最大流改成费用流即可。看起来需要找负环,但容易发现若初始没有负环,那么跑完的残量网络上没有负环(这个证明直接消圈定理。若初始有负环那可能需要后文的有负环费用流算法,但转化后也没有负环),所以正确性显然。
有源汇上下界可行流/最小费用可行流
即源点的 $M\in[-\inf,0]$,汇点的 $M\in[0,\inf]$,并且源点净流出量等于汇点净流入量,那么汇点向源点连容量充分大的边即可。
那么多大是“充分大”呢?根据流的定义,容易发现这条边的流量就是 $s\to t$ 的流量。那么设为最大流上界就足够了。
还是可以换成费用流,看起来需要找一下有没有负权增广路,但容易发现负权增广路加上上面那条边就是负环,和上面的证明类似,也不需要。
有源汇上下界最大流/费用流
先求可行流,然后去掉超级源汇点和那条新加的边在残量网络上跑最大流算法即可。因为显然所有可行流都能不断增广变成最大流。
然后答案就是可行流流量(那条无限边的流量)加上最大流。显然实现时可以直接不删那条边。
然后显然也能换成费用流。
有源汇上下界最小流
这他妈是什么阴间算法。
还是先求可行流。显然此时那条无限边上的流量就是那个可行流的流量。
然后考虑把不需要的流退掉,那么去掉超级源汇和那条无限边后,跑一遍 $t\to s$ 的最大流即可。
答案就是那条无限边减去这个最大流。
注意到这一条没加“/费用流”,因为我不会。
有负环的费用流
这个算法出现在这里必然有它的道理
首先根据消圈定理,若初始无负环则整个费用流求解过程都必定没有负环。
但是如果初始就有负环会导致大部分最短路算法死循环(应该没有最短路算法能处理负环吧?)。
那么考虑进行一些转化使得初始图无负环。容易发现若初始没有负边则显然没有负环。
可以把负费用的边 $(u,v,0,c,w)$(起点,终点,流量下界,容量,费用)视为 $(u,v,c,c,w)$ 和 $(v,u,0,c,-w)$ 两条边,就没有负环了。
另外还有一些神秘构造,比如让它“不要出现环”之类的。不过我还是觉得把负权边全去掉会比较简单。
结语
这篇博客介绍了网络流比较基础的内容,与真正的网络流相比还只是冰山一角,这里引用一句经典的话:
这不是结束,甚至不是结束的开始,只是开始的结束。
网络流学习道阻且长,我也要努力啊!
另:网络流写题记录。