FHQTreap 实现的文艺平衡树
前言
在刷专题时看到这个神奇的算法,然后就学了。
算法详解
大概就是让你维护一个数据结构,最初有一个单调增的排列,然后让你维护多次区间翻转,输出最终序列。
是模板题就不写题目分析了。 因为我也不知道这个算法是什么神仙想出来的。
FHQTreap 维护区间操作的核心思路是利用树的形态维护中序遍历的序列。 具体来说,我们要使得维护后 Treap 的树值不一定满足 BST 的性质,但是树值的中序遍历是我们想要的序列。
只看这道题的区间翻转操作,假如我们原先的序列是 $1-2-3-4-5$,那么建出来的树可能是这样(随机赋堆值,然后因为序列是递增的可以看做满足 BST 性质):
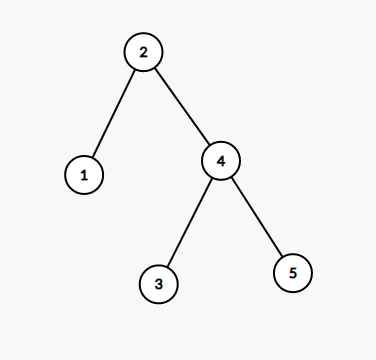
然后考虑翻转后的序列以相同的堆值建树(可以看做满足反过来的 BST):
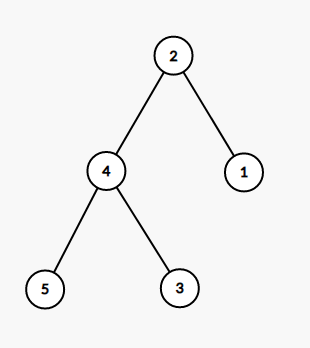
容易发现翻转相当于交换每个结点的左右儿子。
那么就有简单思路了,把要翻转的区间 Split 出来,然后把这一整块所有结点的左右儿子交换。
但是这样复杂度最劣是 $O(m(\log n+n))$ 的,还不如暴力。
回顾一下线段树的单点操作到区间操作经历了什么变化?我们增加了懒标记。那么我们考虑在 FHQTreap 上用懒标记维护交换操作。
具体来说,修改时把要修改的点的懒标记取反,懒标记表示“这个结点所有子孙的左右儿子需要交换”(和线段树懒标记一样,不包括自己),然后修改时记得下传。其实懒标记包括自己也能做这道题,但是就不方便改成在线做法了。
然后需要注意懒标记下传的时间,记住一句话就行:
在访问任何结点信息前都要下传懒标记。
重要的事情说三遍:
在访问任何结点信息前都要下传懒标记。
在访问任何结点信息前都要下传懒标记。
在访问任何结点信息前都要下传懒标记。
然后复杂度是 $O(n\log n)$ 的,和正常 FHQ 是一样的。
参考代码
const int N=5e5+5,inf=0x3f3f3f3f;
int n,m,a[N];
mt19937 mr(time(0));
struct Treap{
private:
int ls[N],rs[N],tv[N],hv[N],mark[N],cntn,root;
int sz[N];
int _New(int val){
int nw=++cntn;
tv[nw]=val;hv[nw]=(unsigned int)mr();
ls[nw]=rs[nw]=0;
mark[nw]=0;sz[nw]=1;
return nw;
}
void _PushUp(int id){
sz[id]=sz[ls[id]]+sz[rs[id]]+1;
}
void _Reverse(int id){
swap(ls[id],rs[id]);
mark[id]^=1;
}
void _PushDown(int id){
if(mark[id]){
if(ls[id]) _Reverse(ls[id]);
if(rs[id]) _Reverse(rs[id]);
mark[id]=0;
}
}
void _Split(int key,int id,int &u,int &v){
if(!id){
u=v=0;
return;
}
_PushDown(id);// (1)!
if(sz[ls[id]]<key){
u=id;
_Split(key-sz[ls[id]]-1,rs[id],rs[u],v);
}else{
v=id;
_Split(key,ls[id],u,ls[v]);
}
_PushUp(id);
}
int _Merge(int u,int v){
if(!u||!v) return u|v;
if(hv[u]>hv[v]){
_PushDown(u);// (2)!
rs[u]=_Merge(rs[u],v);
_PushUp(u);
return u;
}else{
_PushDown(v);
ls[v]=_Merge(u,ls[v]);
_PushUp(v);
return v;
}
}
void _Print(int id){// (3)!
_PushDown(id);
if(ls[id]) _Print(ls[id]);
printf("%d ",tv[id]);
if(rs[id]) _Print(rs[id]);
}
public:// (4)!
void init(){
root=cntn=0;
}
void Build(int N){
forup(i,1,N){
root=_Merge(root,_New(i));
}
}
void Reverse(int L,int R){
int x,y,z;
_Split(L-1,root,x,y);_Split(R-L+1,y,y,z);
_Reverse(y);
root=_Merge(_Merge(x,y),z);
}
void Print(){
_Print(root);
}
}mt;
signed main(){
n=read();m=read();
mt.init();
mt.Build(n);
forup(Case,1,m){
int l=read(),r=read();
mt.Reverse(l,r);
}
mt.Print();
}
- 在访问左右儿子前下传懒标记。
- 这里只用下传 $u$ 的懒标记,因为只访问了 $u$ 的结点信息,下面同理。
- 按中序遍历输出。
- 我是超级封装王
例题
P2042 [NOI2005] 维护数列
简要概括题意,就是改成在线的,然后加了几个无关紧要的操作(((
首先区间推平一样可以用懒标记维护。
然后考虑如何维护最大连续子段和,其实这也很简单,平衡树和线段树有很多共同点,我们可以仿照线段树维护最大连续子段和即可,但是这道题要求子段非空(题目上没明确说,太可恶了),再维护一个最大值即可。
具体来说,除了刚刚说的最大值,还要对每棵子树维护中序遍历上最大前缀和,中序遍历上最大后缀和,中序遍历上最大子段和,子树和,然后就和线段树差不多的合并,需要注意一下平衡树是三个区间合并(左子树,右子树,自己)即可。
另外有个小细节,就是翻转的时候中序遍历上最大前缀和和中序遍历上最大后缀和也需要交换( 这个细节我调了一上午 )。
参考代码
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define forup(i,s,e) for(int i=(s);i<=(e);i++)
#define fordown(i,s,e) for(int i=(s);i>=(e);i--)
using namespace std;
#define gc getchar()
inline int read(){
int x=0,f=1;char c;
while(!isdigit(c=gc)) if(c=='-') f=-1;
while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=gc;}
return x*f;
}
#undef gc
const int N=5e5+5,inf=0x3f3f3f3f;
int n,m,a[N];
mt19937 mr(time(0));
struct Treap{
private:
int ls[N],rs[N],tv[N],hv[N],mark[N],add[N],cntn,root;
int sz[N],sum[N],lsum[N],rsum[N],mxsum[N],mx[N];
int stk[4000005],top;
int _New(int val){
int nw=(top?stk[top--]:++cntn);
tv[nw]=val;hv[nw]=(unsigned int)mr();
ls[nw]=rs[nw]=0;add[nw]=0;
mark[nw]=0;sz[nw]=1;
sum[nw]=val;mx[nw]=val;
lsum[nw]=rsum[nw]=mxsum[nw]=max(val,0);
return nw;
}
void _PushUp(int id){
sz[id]=sz[ls[id]]+sz[rs[id]]+1;
sum[id]=sum[ls[id]]+sum[rs[id]]+tv[id];
lsum[id]=max(lsum[ls[id]],sum[ls[id]]+tv[id]+lsum[rs[id]]);
rsum[id]=max(rsum[rs[id]],rsum[ls[id]]+tv[id]+sum[rs[id]]);
mxsum[id]=max({mxsum[ls[id]],mxsum[rs[id]],rsum[ls[id]]+tv[id]+lsum[rs[id]]});
mx[id]=max({tv[id],mx[ls[id]],mx[rs[id]]});
}
void _Add(int id,int C){
tv[id]=C;
sum[id]=sz[id]*C;
lsum[id]=rsum[id]=mxsum[id]=max(sum[id],0);
mx[id]=C;
add[id]=1;
}
void _Reverse(int id){
swap(ls[id],rs[id]);
swap(lsum[id],rsum[id]);
mark[id]^=1;
}
void _PushDown(int id){
if(mark[id]){
if(ls[id]) _Reverse(ls[id]);
if(rs[id]) _Reverse(rs[id]);
mark[id]=0;
}
if(add[id]){
if(ls[id]) _Add(ls[id],tv[id]);
if(rs[id]) _Add(rs[id],tv[id]);
add[id]=0;
}
}
void _Split(int key,int id,int &u,int &v){
if(!id){
u=v=0;
return;
}
_PushDown(id);
if(sz[ls[id]]<key){
u=id;
_Split(key-sz[ls[id]]-1,rs[id],rs[u],v);
}else{
v=id;
_Split(key,ls[id],u,ls[v]);
}
_PushUp(id);
}
int _Merge(int u,int v){
if(!u||!v) return u|v;
if(hv[u]>hv[v]){
_PushDown(u);
rs[u]=_Merge(rs[u],v);
_PushUp(u);
return u;
}else{
_PushDown(v);
ls[v]=_Merge(u,ls[v]);
_PushUp(v);
return v;
}
}
void _Print(int id){
_PushDown(id);
if(ls[id]) _Print(ls[id]);
printf("%d ",tv[id]);
if(rs[id]) _Print(rs[id]);
}
void _Recovery(int id){
stk[++top]=id;
if(ls[id]) _Recovery(ls[id]);
if(rs[id]) _Recovery(rs[id]);
}
public:
void init(){
top=root=cntn=0;
tv[0]=lsum[0]=rsum[0]=sum[0]=mxsum[0]=sz[0]=0;
mx[0]=-inf;
mark[0]=add[0]=0;
}
void Insert(int P,int *A,int N){
int x,y;
_Split(P,root,x,y);
forup(i,1,N){
x=_Merge(x,_New(A[i]));
}
root=_Merge(x,y);
}
void Erase(int P,int N){
int x,y,z;
_Split(P-1,root,x,y);_Split(N,y,y,z);
_Recovery(y);
root=_Merge(x,z);
}
void Modify(int P,int N,int C){
int x,y,z;
_Split(P-1,root,x,y);_Split(N,y,y,z);
_Add(y,C);
root=_Merge(_Merge(x,y),z);
}
void Reverse(int P,int N){
int x,y,z;
_Split(P-1,root,x,y);_Split(N,y,y,z);
_Reverse(y);
root=_Merge(_Merge(x,y),z);
}
int AskSum(int P,int N){
int x,y,z;
_Split(P-1,root,x,y);_Split(N,y,y,z);
int ans=sum[y];
root=_Merge(_Merge(x,y),z);
return ans;
}
int MaxSum(){
return mxsum[root]?mxsum[root]:mx[root];
}
void Print(){
_Print(root);
}
}mt;
char str[10];
signed main(){
n=read();m=read();
forup(i,1,n){
a[i]=read();
}
mt.init();
mt.Insert(0,a,n);
forup(Case,1,m){
scanf(" %s",str);
if(str[0]=='I'){
int pos=read(),tot=read();
forup(i,1,tot){
a[i]=read();
}
mt.Insert(pos,a,tot);
}else if(str[0]=='D'){
int pos=read(),tot=read();
mt.Erase(pos,tot);
}else if(str[0]=='M'&&str[2]=='K'){
int pos=read(),tot=read(),c=read();
mt.Modify(pos,tot,c);
}else if(str[0]=='R'){
int pos=read(),tot=read();
mt.Reverse(pos,tot);
}else if(str[0]=='G'){
int pos=read(),tot=read();
printf("%d\n",mt.AskSum(pos,tot));
}else{
printf("%d\n",mt.MaxSum());
}
// mt.Print();puts("");
}
}