平衡树入门及 Treap
前言
平衡树是一种非常棒的数据结构,线段树能做的它能做不少,还能查前驱后继,还没有值域限制,空间复杂度还是 $O(n)$ 的,缺点是常数略大,码量也略大,事实上很多时候我都直接把 set 当成平衡树用。另外,其实线段树也可以看做一种只有叶子结点维护信息的特殊的平衡树。
BST
在平衡树之前,我们先看看远处的 BST(Binary Search Tree)吧!
BST 的定义
BST,全称二叉搜索树(Binary Search Tree)。
二叉搜索树是一种二叉树的树形数据结构,其定义如下:
-
空树是二叉搜索树。
-
若二叉搜索树的左子树不为空,则其左子树上所有点的附加权值均小于其根节点的值。
-
若二叉搜索树的右子树不为空,则其右子树上所有点的附加权值均大于其根节点的值。
-
二叉搜索树的左右子树均为二叉搜索树。
摘自 OI Wiki
我们可以对二叉搜索树进行以下操作:
- 插入元素:直接搜到叶子接在叶子上。
- 删除元素:和自己左子树最大的叶子或右子树最小的叶子交换,然后删除它。
- 查询元素排名:从根节点跳到这个值,每次如果向右跳就加上左子树的大小。
- 查询第 $k$ 大: 分左子树,自己,右子树三段考虑。(这个后面会详细说)
- 等等
容易发现 BST 上操作的复杂度和树高正相关,虽然 BST 最好情况下高度是 $O(\log n)$ 的,但我们可以精心构造数据使得 BST 的形态变成这样:
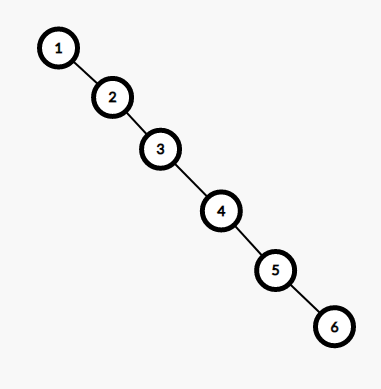
这样各种操作的复杂度就退化成 $O(n)$ 的了。所以我们肯定希望 BST 稍微平衡一点,平衡树就诞生了。
Treap
Treap 是一种比较基础的平衡树,它的名字是树(Tree)和堆(Heap)的合成词,就是说它既满足 BST 的性质也满足二叉堆的性质。
具体来说,我们在每插入一个结点时,除了它作为 BST 的权值,再给它随机一个作为二叉堆的权值,因为在随机数据下堆的期望深度是 $O(\log n)$ 的。然后我们考虑通过某种方法使它第一个权值满足 BST 的性质的同时第二个权值满足二叉堆的性质。
旋转 Treap
顾名思义,旋转 Treap 就是通过旋转操作维护的 Treap。
什么是旋转操作呢?假如我们有这样一棵 BST:
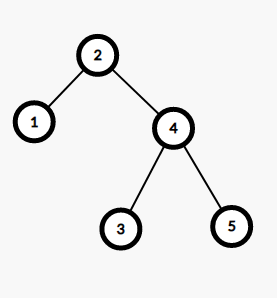
它左旋之后就会变成这样:
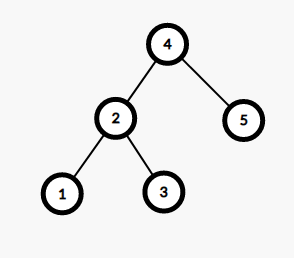
发现没有?它在不改变 BST 性质的条件下改变了结点的上下顺序。
参考代码
然后我们就可以利用旋转操作在不改变 BST 性质的同时维护二叉堆的性质,插入时先插到叶子结点再慢慢旋上去,删除时先旋到叶子结点再直接删除,其余操作和 BST 一样。
完整代码就不贴了,主要是我不太喜欢旋转 Treap
FHQ Treap
FHQ Treap(范浩强 Treap),即无旋 Treap,是一种基于分裂(split)和合并(merge)操作维护的 Treap。
FHQ Treap 码量比旋转 Treap 小,写起来更直观,更好理解,但缺点是常数略大。鉴于现在 CCF 在尽力减小常数对考生成绩的影响,我更推荐学习 FHQ Treap。
首先我们整理一下每个结点要维护哪些信息:
- 左右儿子(下文代码中
l,r)。 - 作为 BST 的权值(下文代码中
tv)。 - 作为二叉堆的权值(下文代码中
hv)。 - 其它要维护的值(比如 P3369 【模板】普通平衡树 需要维护子树大小,即下文代码中
sz)。
基本操作
这是一些非常基本,而且一眼就能看懂的操作。
新建结点与合并子树信息
mt19937 mr(time(0));
int rd(){// (4)!
return (unsigned long long)mr()%998244853;
}
int cntn,root;// (1)!
int New(int x){// (2)!
int nw=++cntn;
hv[nw]=rd();
tv[nw]=x;
sz[nw]=1;
l[nw]=r[nw]=0;
return nw;
}
void PushUp(int id){// (3)!
sz[id]=sz[l[id]]+sz[r[id]]+1;
}
- 结点数量,根结点。
- 新建结点。
- 合并操作。
- 随机数生成。
分裂(split)操作
分裂操作有两种,按值分裂和按大小分裂,这里因为我的 Treap 不需要按大小分裂就不提了,只说按值分裂。
以这样一棵树为例:
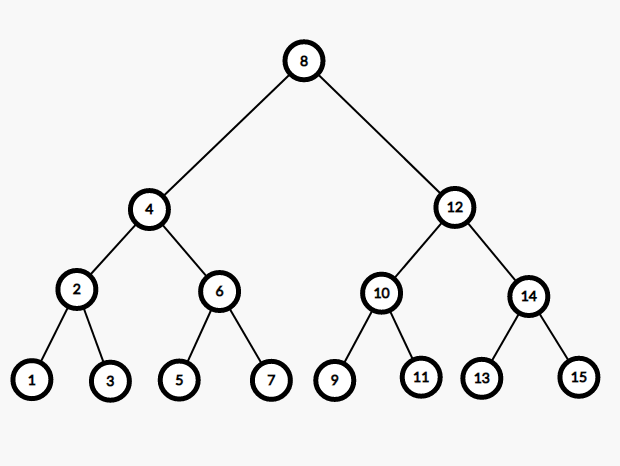
假如我们要按 $5$ 分裂,即分裂成两棵树,其中一棵 $T_1$ 所有权值均小于等于 $5$,另一棵 $T_2$ 均大于 $5$。
分出来就是这样:
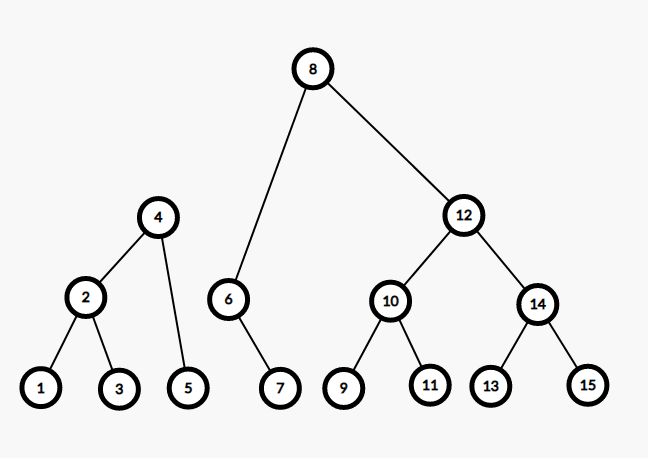
考虑分裂的过程是什么样的。
首先从根节点进入,发现根节点 $8>5$,说明根节点及其整个右子树都属于 $T_2$,而左子树里较大的可能也属于 $T_2$,继续往左子树分离。
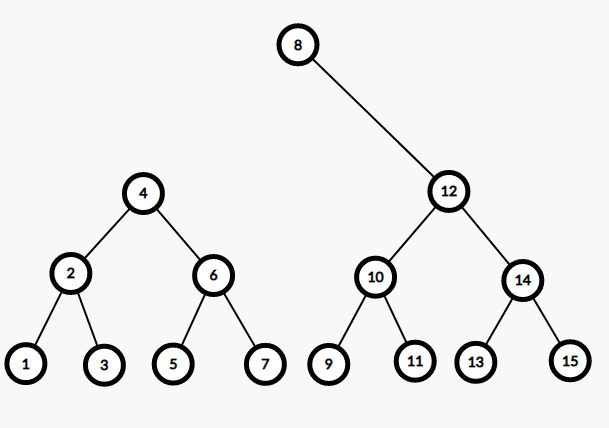
然后进入左子树,发现根节点 $4 \le 5$,说明根节点及其整个左子树都属于 $T_1$,继续往右子树分离。
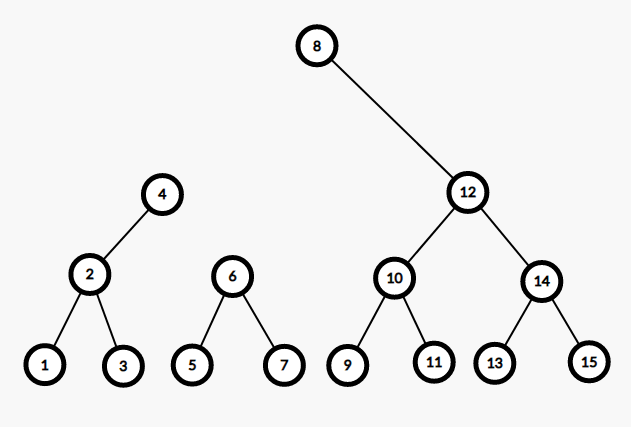
发现 $6>5$,连进 $T_2$,往左子树分离。
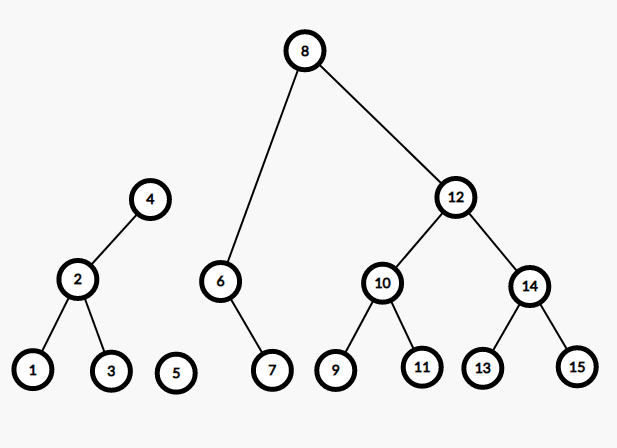
发现 $5 \le 5$,连进 $T_1$,往右子树分离。

发现不存在右子树,操作结束。
利用 C++ 的引用特性,我们可以非常优雅地实现这个过程:
参考代码
void Split(int id,int key,int &x,int &y){
if(!id){
x=y=0;
}else if(tv[id]<=key){
x=id;
Split(r[id],key,r[x],y);
PushUp(id);// (1)!
}else{
y=id;
Split(l[id],key,x,l[y]);
PushUp(id);
}
}
- 所有的修改操作后一定记得合并子树信息。
合并(merge)操作
由于我们维护的是一棵平衡树,分裂之后肯定要合并回去,我们就是要在合并的时候维护二叉堆的性质。
我们合并的时候假定 $T_1$ 中所有数都小于 $T_2$,注意到分裂的过程完全可以保证这个性质。所以我们合并的时候只用额外考虑二叉堆的性质即可。由于 $T_1$ 中所有数都小于 $T_2$,每次要么把 $T_1$ 中的结点 $x$ 放在 $T_2$ 中的结点 $y$ 的左子树,要么把 $y$ 放在 $x$ 的右子树。
假如我们分裂后有两棵这样的树,结点旁的红字为堆权。
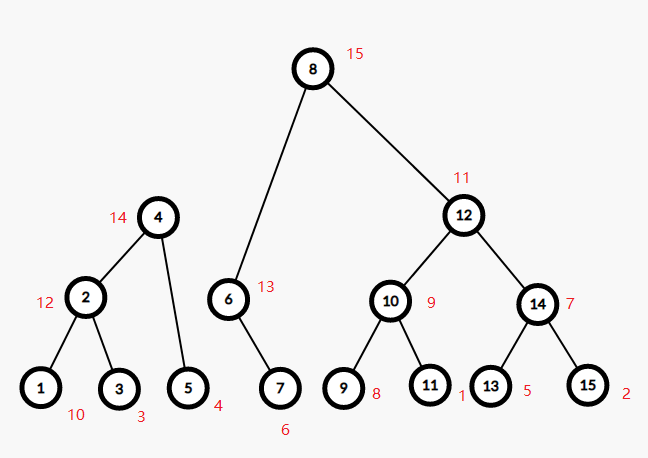
最开始考虑两根结点 $4,8$,发现 $14<15$,左边的当儿子,考虑以 $4,6$($6$ 即 $8$ 的左儿子)为根结点的两子树合并。
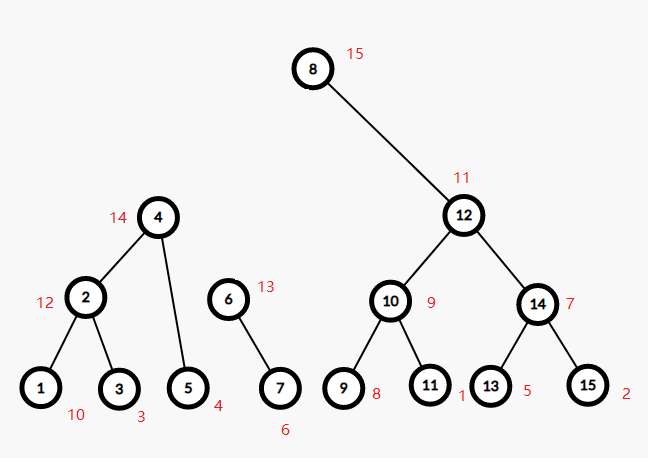
发现 $14>13$,右边的当儿子,考虑 $5,6$($5$ 即 $4$ 的右儿子)为根结点的两子树合并。
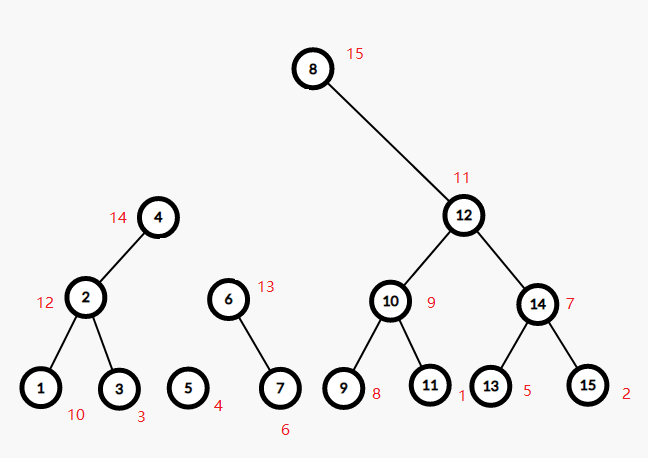
发现 $4<13$,左边的当儿子,考虑 $5,7$ 为根的两子树合并。
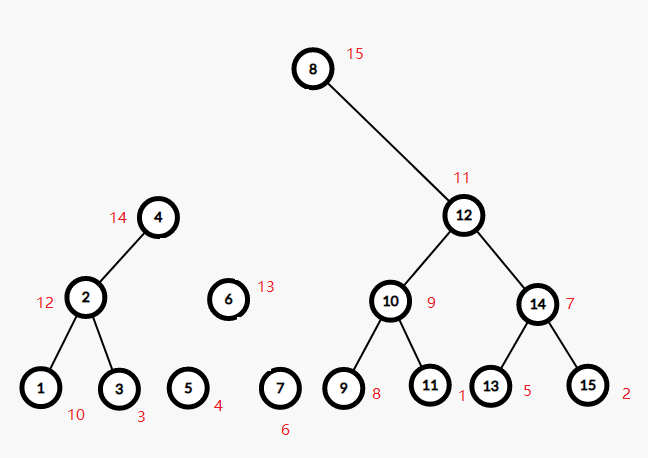
发现 $4<6$,左边的当儿子,考虑 $5$ 和 $7$ 的左儿子为根的两子树合并。
发现 $7$ 没有左儿子,结束查询,回溯时连边。
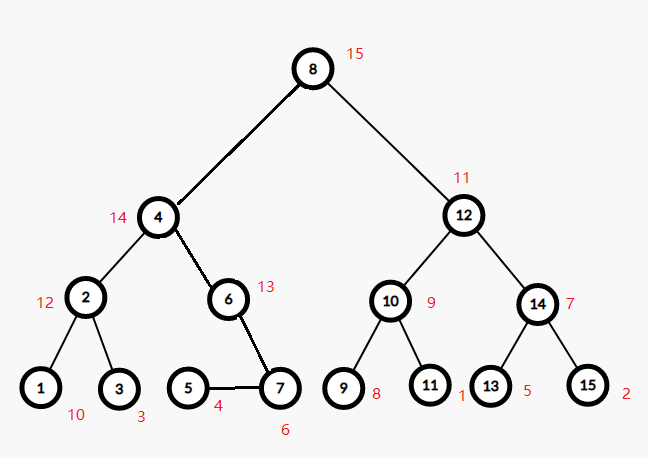
其中 $5$ 是 $7$ 的左儿子。
容易发现这样在保持 BST 性质的同时维护了二叉堆的性质。
写成代码就是这样:
参考代码
int Merge(int x,int y){// (1)!
if(!x||!y){
return !x?y:x;
}else if(hv[x]>hv[y]){
r[x]=Merge(r[x],y);
PushUp(x);
return x;
}else{
l[y]=Merge(x,l[y]);
PushUp(y);
return y;
}
}
- 返回值是以 $x,y$ 为根的两树合并后的根结点。
基于这两个操作,我们可以优雅地完成其它操作。
其它操作
插入
要插入一个值 $key$,只需要把原树按 $key-1$ 分裂成两棵树,再为 $key$ 新建一个结点,把这三棵树合并起来。
删除
删除类似,把原数先按 $key$ 分裂成 $T_1,T_2$,再把 $T_1$ 按 $key-1$ 分裂成 $T_3,T_4$。需要注意此时 $T_4$ 中可能有多个值为 $key$ 的结点。我们可以把 $T_4$ 的根结点的儿子的子树合并起来,这样就能实现只删一个,然后把 $T_3,T_4,T_2$ 按顺序合并。如果要删除所有值为 $key$ 的结点的话直接把 $T_3,T_2$ 合并起来即可。
参考代码
void Erase(int key){
int x,y,z;
Split(root,key-1,x,y);
Split(y,key,y,z);
y=Merge(l[y],r[y]);// (1)!
root=Merge(Merge(x,y),z);
}
- 如果题目没有保证要删东西的一定存在这里需要特判一下。
查询排名
普通平衡树题面中告诉我们排名就是比它小的数的数量加一。我们可以把原树按 $key-1$ 分裂后查询左树的大小再加一即可。
参考代码
int Rank(int key){
int x,y,ans;
Split(root,key-1,x,y);
ans=sz[x]+1;
root=Merge(x,y);// (1)!
return ans;
}
- 分裂了一定记得合并回去。
查询排名 XX 的数
假如按大小分裂这个操作有一个非常优雅的写法。但是那样的话所有操作只有这一个必须要按大小分裂,得不偿失,不如直接用 BST 的的写法。
参考代码
int _At(int rk,int id){
if(rk==sz[l[id]]+1) return tv[id];// (1)!
else if(rk<=sz[l[id]]) return _At(rk,l[id]);
else return _At(rk-sz[l[id]]-1,r[id]);
}
int At(int rk){// (2)!
return _At(rk,root);
}
- BST 上二分要分成左子树,自己,右子树三部分考虑。
- 我得了一种数据结构不封装就想似的病。
求前驱,后继
前驱可以直接按 $key-1$ 分裂后找到左树最大值,后继可以按 $key$ 分裂后找右树最小值。
参考代码
垃圾回收优化
发现原来的写法某结点删除后就不会再利用它,这样非常不好,空间常数更大,由于内存访问不连续时间常数也更大,考虑用一个栈存储删掉的结点,新增结点时优先考虑利用之前删掉的那个。
改动 New 和 Erase
实践证明这样并不会使时间减慢。

总结
平衡树这个东西,一般不会用到,但是不怕一万只怕万一啊。