LCT 学习笔记
前言
由于 Splay 除了写 LCT 少个 $\log$ 以外被 FHQ 全方面薄纱(常数,好写程度,易错率,还有不能可持久化),干脆就写一起了。
LCT 以前感觉巨大困难啊,但是熟悉了就简单了。
Splay 树
先讲讲 LCT 所需要用到的 Splay 树部分。
Splay 树是一种平衡树,核心在 splay(伸展)操作,利用伸展操作使得势能分析后复杂度是 $O(n\log n)$ 的。
核心操作
splay 的实现基于 rotate 操作。rotate 操作类似于有旋 Treap 的 Zig/Zag 操作,可以在不改变 BST 性质的情况下改变树的形态:
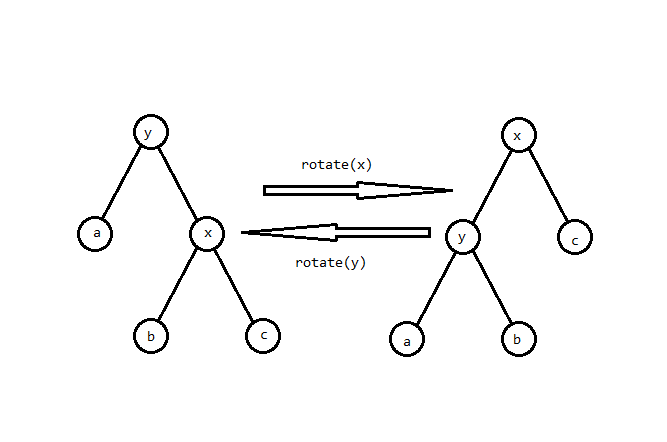
rotate(x) 的意思是“把 $x$ 向上旋转”。
实现比较简单:
参考实现
然后就是 splay 操作。splay 操作的目的是通过若干次 rotate 操作把 $x$ 旋转到根,分三种情况(下文默认 $y=fa_x$):
-
$y$ 就是根:
此时一次 rotate 就能旋到根:
图就是上面那张,就不再放一遍了。
这种操作叫 Zig/Zag。
-
$y$ 和 $x$ 是父亲的同一个儿子
就是这种情况:
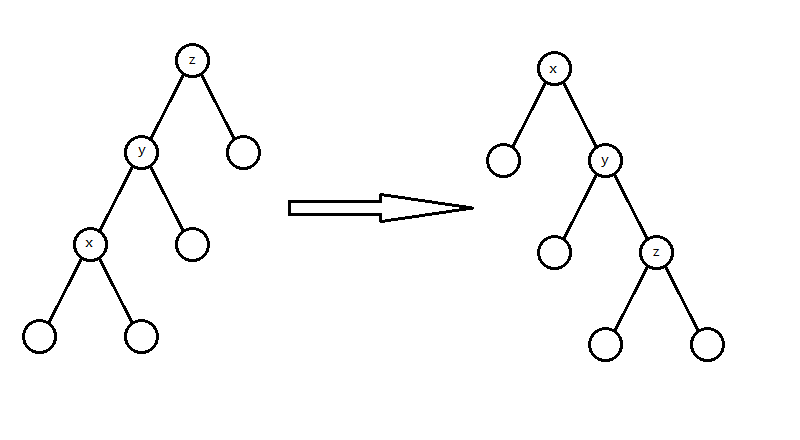
这种情况先
rotate(y)再rotate(x),据说在势能分析下很平衡。这种操作叫 Zig-Zig/Zag-Zag。
-
$y$ 和 $x$ 是父亲的不同儿子
这种情况:
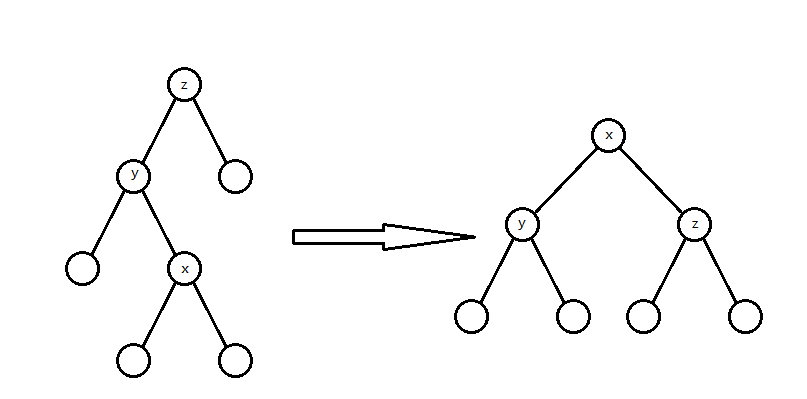
这种情况
rotate(x)两次即可,看起来就很平衡。这种操作叫 Zig-Zag/Zag-Zig。
代码实现很简单:
其余操作
其余就比较简单了,注意每次访问一个结点就 splay 到根(因为 Splay 树的复杂度是“splay 操作的复杂度在势能分析下的复杂度”,我们需要每次操作都 splay 一下,保证每个操作的复杂度始终是 splay 的复杂度),然后删除可以 splay 到根后用类似 FHQ 的写法把两子树合并。基本上会 FHQ 的都能写,此处略过(因为在 LCT 中不重要)。
复杂度证明
LCT
LCT,全称 link-cut tree( 林克卡特树,意思是玩塞尔达特别容易卡到树上 )中文貌似没有译名。我们可以用它解决动态树问题。
维护一棵树,支持如下操作:
- 修改两点间路径权值。
- 查询两点间路径权值和。
- 等等能用树剖维护的树链信息。
这是一道树剖模版题。
但是再加一个操作:
- 断开并连接一些边,保证仍是一棵树。
要求在线求出上面的答案。
这就成了动态树问题,可以使用 LCT 求解。
(另外子树问题貌似可以用 ETT 解决,留坑待补)
回顾一下树剖(重链剖分)
考虑树剖是对每个结点保留一条重边,然后对每一条连续的重链开一个数据结构,但因为一些奇妙的性质可以只用一棵线段树维护完。
所以提炼一下,其实就是把树分解成垂直的链,并用数据结构维护每条链的信息。
实链剖分
考虑重剖不是很动态啊,所以我们使用更自由的实链剖分。
具体来说,对每个点指定一个“实儿子”(也可能没有),然后对每一条实链维护数据结构。请记住我们选择实链剖分的最重要的原因:它是我们自己选择的,灵活且可变。正是它的这种灵活可变性,我们采用 Splay Tree 来维护这些实链。
正文
(乐,算法引入怎么这么长)
我们可以简单的把 LCT 理解成用一些 Splay 来维护动态的实链剖分,以期实现动态树上的区间操作。对于每条实链,我们建一个 Splay 来维护整个链的信息,其中 Splay 的中序遍历就是实链从上到下的路径。然后再连若干条虚边表示多条实链之间的相对关系。
我们想要维护的大概是这么一个东西:
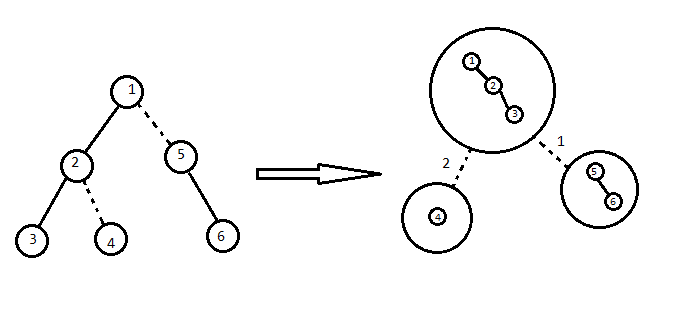
然而事实上不需要这么麻烦,注意到一棵 Splay 的根处的 $fa$ 是空的,那么可以考虑直接用根节点的 $fa$ 存储虚边。具体来说,对于每条 Splay 的根,我们将它的 $fa$ 赋为对应实链顶端结点的父亲。
大概是这样(通常形态不唯一,这是一种可能的情况):
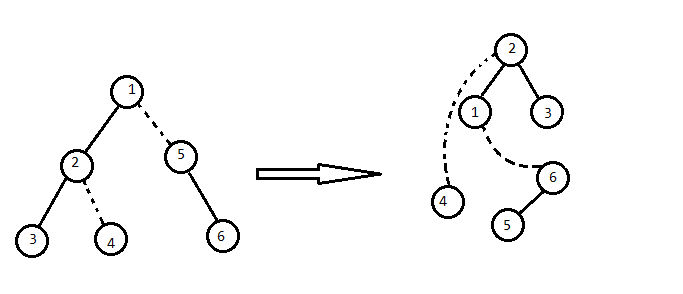
注意虚边在父亲处不指向儿子!
我们称这一棵 Splay 与虚边构成的树为辅助树,为了区分,称原本的树为原树,那么根据定义,辅助树需要具有以下性质(其实刚刚提过,这里整合一下):
- 辅助树上的点与原树的点一一对应
- 辅助树由多棵 Splay 组成,每棵 Splay 维护原树中的一条路径,且中序遍历这棵 Splay 得到的点序列,从前到后对应原树从上到下的一条路径。
- 辅助树的各棵 Splay 之间并不是独立的。每棵 Splay 的根节点的父亲节点本应是空,但在 LCT 中每棵 Splay 的根节点的父亲节点指向原树中这条链的父亲节点(即链最顶端的点的父亲节点)。这类父亲边与通常 Splay 的父亲边的区别在于儿子认父亲,而父亲不认儿子,对应原树的一条虚边。因此,每条实链恰好有一个点的父亲节点为空(这个点是原树上该实链的根节点对应的辅助树结点所在 Splay 的根)。
- 辅助树是可以在满足辅助树、Splay 的性质下任意换根的。
- 虚实链变换可以轻松在辅助树上完成,这也就是实现了动态维护树链剖分。
由于辅助树的以上性质,我们维护任何操作都不需要维护原树,辅助树可以在任何情况下拿出一个唯一的原树,我们只需要维护辅助树即可。
核心操作
LCT 的核心操作有两个(其实真正核心的只有一个),但在此之前要先介绍特化的 rotate 和 splay 操作:
参考代码
#define get(x) (ch[fa[x]][1]==x)
#define isRoot(x) (ch[fa[x]][0]!=x&&ch[fa[x]][1]!=x)
void Rotate(int x){
int y=fa[x],z=fa[y],ss=get(x);
if(!isRoot(y)) ch[z][y==ch[z][1]]=x;
ch[y][ss]=ch[x][!ss];fa[ch[x][!ss]]=y;
ch[x][!ss]=y;fa[y]=x;fa[x]=z;
PushUp(y);PushUp(x);
}
void Update(int x){
if(!isRoot(x)) Update(fa[x]);
PushDown(x);
}
void Splay(int x){
Update(x);
for(int f=fa[x];f=fa[x],!isRoot(x);Rotate(x)){
if(!isRoot(f)) Rotate(get(x)==get(f)?f:x);
}
}
首先是宏定义的 isRoot 函数。这个很简单,因为若 $x$ 的父亲两个儿子都不是它,说明这是一条虚边,即 $x$ 是所在 Splay 的根。
然后 rotate 和 Splay 树差不多,注意要先特判 $y$ 是不是根(这个很重要,不然会把 $x$ 转到奇怪的地方)。
最后是 splay 操作。由于任何树形数据结构下传标记都是从上到下的,但 LCT 会从下到上操作。那么就需要在操作前先行下放标记(就是 Update 函数)。
- access 操作
access 操作的目的是将 $x$ 到所在连通块根节点的路径变为一条实链。
具体如何操作呢?考虑辅助树上 $x$ 到根路径中的所有 Splay。
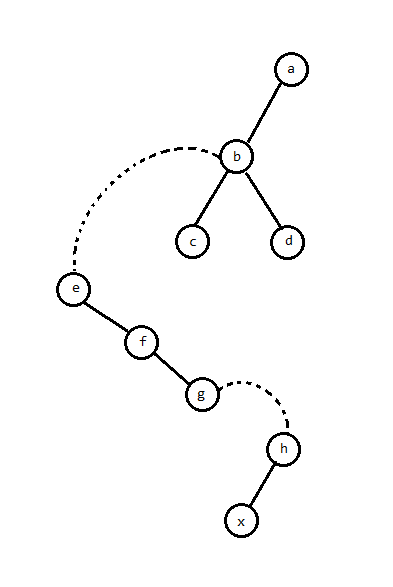
“变为一条实链”就等价于把路径上的虚边变成实边,并且删掉不需要的实边。
考虑虚边在原树上的意义,那么变成的实边在辅助树上必定是若干个右儿子。那么我们可以把所有虚边连到的父亲 splay 到对应 Splay 的根:
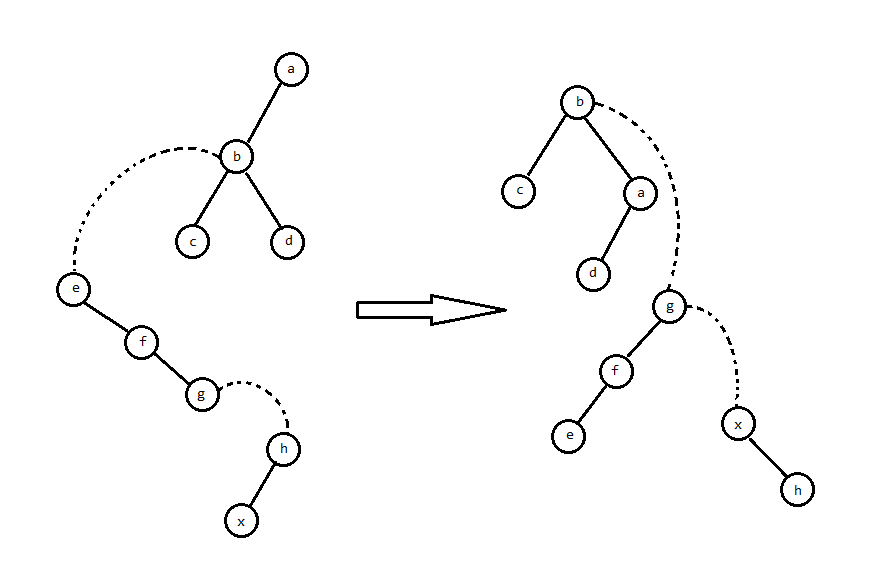
然后把虚边变成右儿子,原本的右儿子自然就成了虚边:
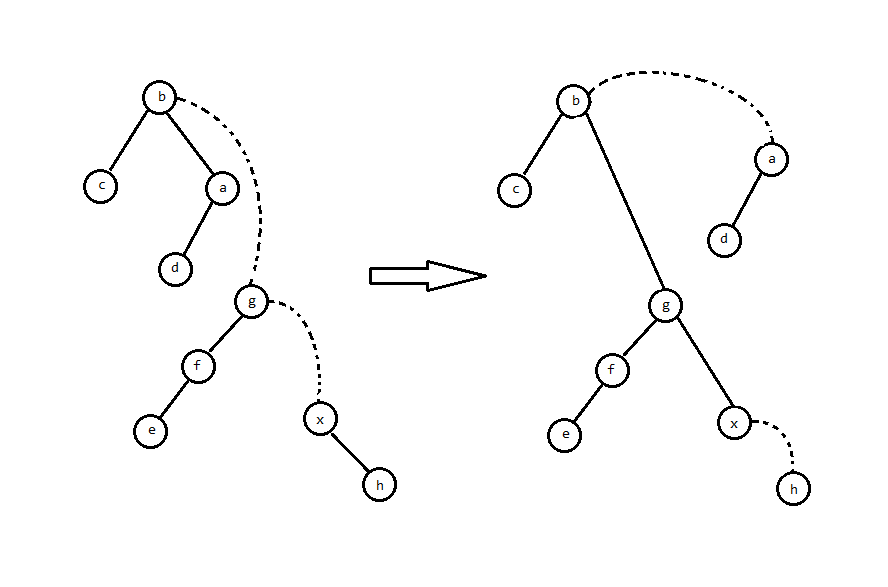
就做完了。
让我们看看原树的表现:
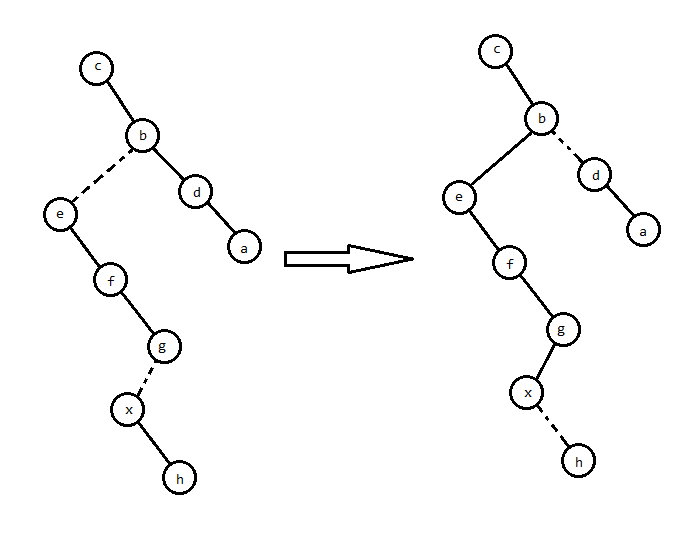
显然是对的。
这个返回值 $p$ 是这一棵 Splay 的根。
- makeroot 操作
顾名思义,将 $x$ 变为对应连通块的根。
考虑换根会使哪些点的深浅相对关系改变,容易发现就是原来的根到新根的路径。
那么 access 后进行平衡树的翻转操作即可。
参考代码
- 这个标记记得在
PushDown中下传。
其余操作
LCT 通常都是解决链上问题的。那么其余操作一遍都是对链操作/查询,所以只要把链取出来就行了。具体步骤就是将链的一个端点变成根,然后 Access 另一个。
最后是 link/cut 操作。
- link 操作
把其中一边变成对应连通块的根,然后连一条虚边即可。
但是有可能需要判两点是不是原本就连通。这个有很多种实现。一种是找两点对应连通块的根是否相同,这个可以 Access(x) 后一直向左儿子走:
参考代码
- cut 操作
MakeRoot(x) 后 Access(y),此时(如果该边存在)那么 $y$ 必定是 $x$ 的右儿子(显然),并且 $y$ 没有左儿子(否则说明 $x,y$ 之间还有其它结点)。那么把这条边删掉即可。
参考代码
然后就完啦。
复杂度证明
留坑待补。